Hva er dynamisk balanse? (Med eksempel)

Han Dynamisk balanse Det er staten der et mobilobjekt ideelt er representert som en partikkel når bevegelsen er ensartet rettlinjet. Dette fenomenet oppstår når summen av eksterne krefter som virker på det, blir kansellert.

Det antas vanligvis at hvis det ikke er noe nett eller resulterende kraft på et objekt, er hvile den eneste mulige konsekvensen. Eller også at for at en kropp skal være i balanse, skal det ikke være noen styrke som handler.

Figur 1. Denne katten beveger seg i dynamisk likevekt hvis den gjør det med konstant hastighet. Kilde: Pixabay.

Egentlig er balansen fravær av akselerasjon, og derfor er den konstante hastigheten perfekt mulig. Katten i figuren kan bevege seg uten akselerasjon.

Et objekt som har ensartet sirkulær bevegelse er ikke i dynamisk likevekt. Selv om hastigheten er konstant, er det en akselerasjon rettet mot midten av omkretsen som holder den i banen. Denne akselerasjonen er ansvarlig for å endre riktig til hastighetsvektoren.

Nullhastighet er en spesiell situasjon for balansen mellom en partikkel, som tilsvarer å bekrefte at objektet er i ro.

Når det gjelder objekter som en partikkel, er det en veldig nyttig idealisering når du beskriver deres globale bevegelse. Faktisk er de mobile objektene som omgir oss sammensatt av et stort antall partikler hvis individuelle studier ville være tungvint.

[TOC]

Superposisjonsprinsippet

Dette prinsippet gjør det mulig å erstatte virkningen av flere krefter på et objekt med en ekvivalent kalt den resulterende kraften kald eller nettokraft FN, og at i dette tilfellet er ugyldig:

F1 +F2 +F3 +.. . = Fr = 0

Der krefter f1, f2, f3 .. ., FI er de forskjellige kreftene som virker på kroppen. Sumory notation er en kompakt måte å uttrykke den på:

Så lenge en ubalansert kraft ikke griper inn, kan objektet opprettholdes på ubestemt tid med konstant hastighet, siden bare en styrke kan endre dette panoramaet.

Når det gjelder komponentene i den resulterende kraften, uttrykkes den dynamiske likevektstilstanden til en partikkel som følger: FX = 0; Fy = 0; Fz = 0.

Rotasjon og balanseforhold

For partikkelmodellen er tilstand FR = 0 tilstrekkelig balansegaranti. Når du tar hensyn til dimensjonene til mobilen som studeres, er det imidlertid muligheten for at objektet kan rotere.

Rotasjonsbevegelsen innebærer eksistensen av en akselerasjon, derfor er de roterende kroppene ikke i dynamisk likevekt. En kropps sving trenger ikke bare deltakelse av en styrke, men det er nødvendig å bruke det praktiske nettstedet.

For å sjekke det, kan du plassere en tynn stang med lengde på en overflatefri friksjon, for eksempel en isete overflate eller et veldig polert speil eller glass. De normale balansene til vekten vertikalt, og når du bruker to krefter F1 og F2 i samme størrelse, i henhold til diagrammet over følgende figur, hva som skjer:

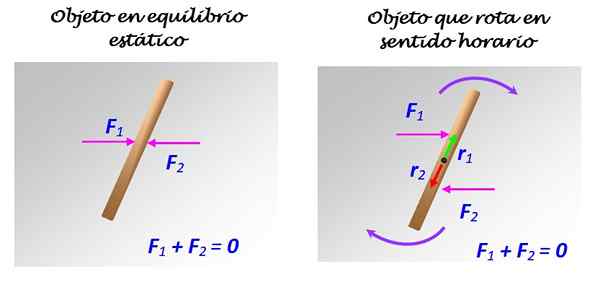Figur 2. En stang på en overflate uten friksjon kan være eller ikke være i balanse, avhengig av hvordan kreftene 1 og 2 blir brukt. Kilde: Selvlaget.

Hvis F1 og F2 gjelder som vist til venstre, med en felles handlingslinje, vil stangen forbli i ro. Men hvis F1 og F2 gjelder som vist til høyre, med forskjellige handlingslinjer, selv om den er parallell, oppstår en rotasjon i en plan, rundt aksen som passerer gjennom sentrum.

I dette tilfellet utgjør F1 og F2 et par styrker eller bare et par.

Dreiemoment eller kraftmoment

Effekten av dreiemomentet er å produsere en rotasjon på et utvidet objekt som eksempelstangen. Vektorstørrelsen som er ansvarlig kalles dreiemoment eller også et øyeblikk av en kraft. Det er betegnet som τ og beregnes av:

τ = r x f

I dette uttrykket f er den påførte kraften og r er vektoren som går fra rotasjonsaksen til påføringspunktet av kraften (se figur 2). Retningen på τ er alltid vinkelrett på planet der f og r ligger og dets enheter i det internasjonale systemet er n.m.

For eksempelet er retningen til øyeblikkene produsert av F1 og F2 mot papiret, i henhold til reglene for vektorproduktet.

Selv om kreftene avbryter hverandre, gjør ikke deres dreiemomenter. Og resultatet er rotasjonen som vises.

Likevektsforhold for et utvidet objekt

Dette er to forhold som må være oppfylt for å garantere balansen til et utvidet objekt:

Løst eksempel

Du har en skuff eller bagasjerom som veier 16 kg-f, som glir gjennom et skrå plan med konstant hastighet. Kilehellingsvinkelen er θ = 36º. Svare:

a) Hva er størrelsen på den dynamiske friksjonskraften som er nødvendig for at bagasjerommet kan gli med konstant hastighet?

b) Hvor mye er den kinetiske friksjonskoeffisienten?

c) Hvis høyden H på det skrå planet er 3 meter, finn nedstigningen på bagasjerommet, vel vitende om at det tar 4 sekunder å nå bakken.

Løsning

Bagasjerommet kan behandles som om det var en partikkel. Derfor vil kreftene gjelde på et punkt som ligger omtrent i sentrum, som all dens masse kan antas. Det er til dette punktet at sporet vil bli fulgt.

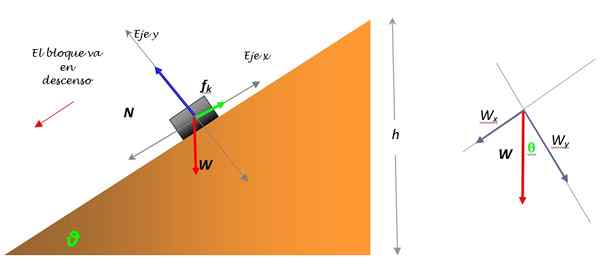Figur 3. Gratis kroppsdiagram for bagasjerommet som glir nedoverbakke og nedbrytning av vekt (til høyre). Kilde: Selvlaget.

Vekten W er den eneste kraften som ikke faller på en av koordinataksene og må deles inn i to komponenter: WX og WY. Denne nedbrytningen er vist i ordningen (figur 3).

Det er også praktisk å gi vekten til enhetene i det internasjonale systemet, som det er nok til å multiplisere med 9.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Avsnitt a

Gjennom den horisontale aksen er den horisontale komponenten i WX -vekten og FK -dynamisk eller kinetisk friksjonskraft, som motsetter seg bevegelsen.

Å velge den positive sansen i retning av bevegelsen, er det lett å legge merke til at det er WX som er ansvarlig for at blokken går nedoverbakke. Og ettersom friksjonen er imot, i stedet for å gli raskt, har blokken muligheten for å gli konstant nedoverbakke.

Den første likevektstilstanden er tilstrekkelig, siden vi behandler bagasjerommet som en partikkel, som er sikret i uttalelsen som er i dynamisk likevekt:

WX - FK = 0 (det er ingen akselerasjon i den horisontale adressen)

FK = 92.2 n

Avsnitt b

Størrelsen på dynamisk friksjon er konstant og er gitt av FK = μk n. Dette betyr at den dynamiske friksjonskraften er proporsjonal med normal og størrelsen på dette er nødvendig for å kjenne friksjonskoeffisienten.

Når vi observerer det frie kroppsdiagrammet, kan det sees at vi på den vertikale aksen har normalkraften N, som kilen utøver på bagasjerommet og er rettet oppover. Hun er balansert med den vertikale komponenten i vekten wy. Å velge opp som en positiv forstand og bruke Newtons andre lov og balansestatusresultatene:

N - WY = 0 (det er ingen bevegelse langs den vertikale aksen)

Derfor:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2 /126.9 = 0.73

Avsnitt C

Den totale avstanden som ble reist ved bagasjerommet fra toppen av kilen til bakken, finnes av trigonometri:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

For å beregne hastigheten brukes definisjonen for ensartet rettlinjet bevegelse:

V = d/t = 5.1 m/4 s = 1.3 m/s

Referanser

1. Rex, a. 2011. Fundamentals of Physics. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning. 120 - 124.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9na red. Cengage Learning. 99-112.
4. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fysikk. Addison Wesley. 148-164.