Hva er skjæring, stivhet eller skjærmodul? (Løste øvelser)

Han Kutt modul Beskriv et materials svar på anvendelsen av en skjærinnsats som deformerer den. Andre hyppige kirkesamfunn for skjæremodulen er skjær, saks, tverrgående elastisitet eller tangensiell elastisitetsmodul.

Når innsatsen er liten, er deformasjonene proporsjonale med dem, i henhold til Hooke's lov, kuttekonstanten er proporsjonalitetskonstanten. Derfor:

Kutt modul = kutting/deformasjonsinnsats

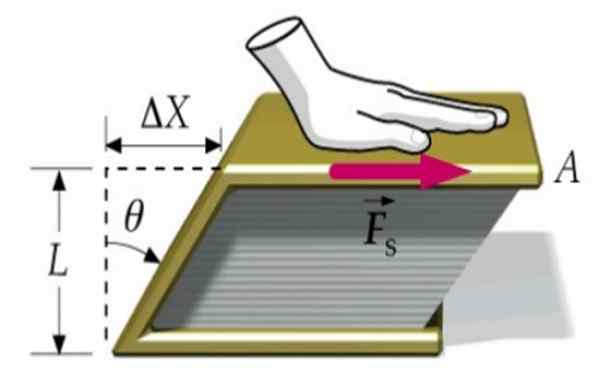
Figur 1. En bok er deformert takket være Tangential Force FS. Kilde: f. Zapata.

Anta at en kraft blir brukt på lokket til en bok, og er den andre festet på overflaten av bordet. På denne måten beveger ikke boka som helhet seg, men deformeres når det øvre lokket beveger seg med hensyn til det nedre i mengden Δx.

Boken går fra å ha en rektangulær tverrsnitt til en seksjon i form av parallellogram, som vi ser i det overordnede bildet.

Være:

τ = f/a

Innsatsen eller skjærespenningen, være F størrelsen på den påførte kraften og TIL Området det opptrer på.

Deformasjonen forårsaket er gitt av kvotienten:

Δ = Δx / l

Derfor er skjæringsmodulen, som vi vil betegne som G,:

På denne måten er skjæringsmodulen ansvarlig for å måle motstanden til interiørplanene til objektet som er parallelt med den anvendte innsatsen.

Og ettersom ΔX / L mangler dimensjoner, er enhetene til G de samme som av skjæreinnsatsen, og det er grunnen mellom styrken og området.

I det internasjonale systemet med enheter er disse enhetene Newton/Square Metro eller Pascal, forkortet PA. Og i Anglo -Saxon -enheter er det pund /kvadratmeter, forkortet psi.

[TOC]

Kan tjene deg: ensartet rettlinjet bevegelse: egenskaper, formler, øvelser

Kutt modul for forskjellige materialer

Under handlingen av å kutte krefter som de beskrevne, tilbyr objekter en motstand som ligner på boken, der de indre lagene glir. Denne typen deformasjon kan bare forekomme i faste kropper, som har tilstrekkelig stivhet til å motsette seg å bli deformert.

På den annen side tilbyr væsker ikke denne typen motstand, men de kan oppleve volumdeformasjoner.

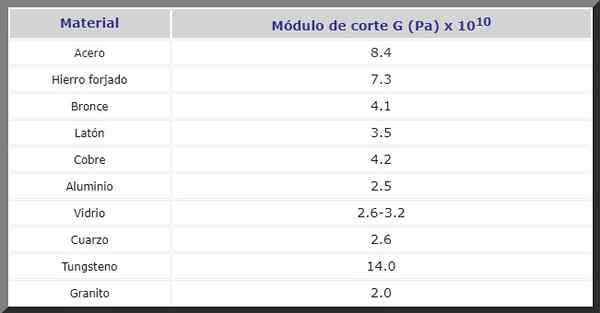
Figur 2. Bolter i strukturer er gjenstand for kutteinnsats. Kilde: Pixnio.

Deretter har du G -Cut -modulen i P for forskjellige materialer som ofte brukes under konstruksjon og i fremstilling av maskiner og reservedeler av alle slag:

Eksperimentelt mål på skjæringsmodulen

For å finne verdien av skjæremodulen, må du teste prøver av hvert materiale og undersøke svaret ditt på anvendelsen av en skjæreinnsats.

Prøven er en stang laget med materialet, med radio R og lengde L kjent, som er fast i den ene enden, mens den andre kobles til aksen til en fri remskive.

Remskiven har et tau bundet, hvis frie ende et veier er hengt som utøver en kraft F På stangen gjennom tauet. Og denne styrken produserer på sin side et øyeblikk M I stangen, som deretter vender en liten vinkel θ.

Et monteringsskjema kan sees i følgende figur:

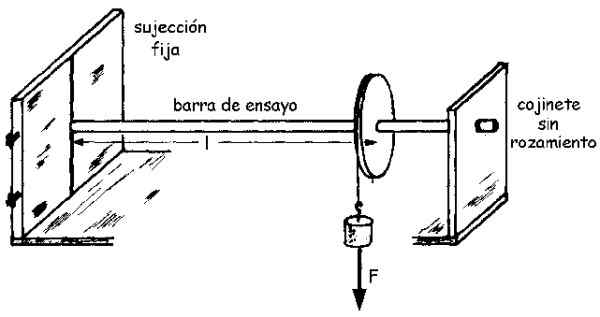Figur 3.- Eksperimentell enhet for å bestemme skjærmodulen eller kuttet i en tynn teststang. Kilde: University of Valladolid.

Øyeblikkets størrelse M, som vi betegner som M (uten fet skrift) er relatert til vinkelen rotert θ gjennom kuttmodulen g i henhold til følgende ligning (den blir trukket av et enkelt integral):

Ettersom størrelsen på øyeblikket er lik produktet fra kraften F -modulen med remskiven R -radius_p:

Det kan tjene deg: torricelli eksperiment: atmosfærisk trykkmål, betydning

M = f.R_p

Og kraft er vekten som henger W, så:

M = w.R_p

Erstatte i ligningen av størrelsen på øyeblikket:

Du har forholdet mellom vekt og vinkel:

Hvordan finne G?

Dette forholdet mellom variabler W og θ Det er lineært, så de forskjellige vinklene som er produsert som henger forskjellige vekter, måles.

Parene med vekt og vinkel er grafer på et millimeterpapir, den beste linjen som passerer gjennom eksperimentelle punkter blir justert og skråningen beregnes m av nevnte linje.

 Derfra følger det det:

Øvelser med løsning

- Oppgave 1

En 2 stang.5 meter lang og radio 4.5 mm er fikset i den ene enden. Den andre kobles til en 75 cm radioskive som har en 1 1 vekt.3 kg. Den vendte vinkelen er 9.5. plass.

Med disse dataene blir det bedt om å beregne kuttmodulen G for stangen.

Løsning

Fra ligningen:

Gasses G:

Og verdiene gitt i uttalelsen erstattes, og er forsiktig med å uttrykke alle dataene i det internasjonale systemet med enheter hvis:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_p = 75 cm = 0.075

Å flytte fra kilo (de er faktisk kilo - kraft) til Newton multiplies med 9.8:

W = 1.3 kg-kraft = 1.3 x 9.8 n = 12.74 n

Og til slutt må gradene være på radianer:

9.5. = 9.5 x2π /360 radianer = 0.1658 radianer.

Med alt dette har du:

= 2.237 x 10¹⁰ Pa

- Oppgave 2

En gelkube er 30 cm side. Et av ansiktene er fikset, men samtidig brukes en parallell kraft på 1 N på motsatt ansikt, som takket være dette flytter 1 cm (se eksemplet på boken i figur 1).

Det kan tjene deg: magnetisering: orbital og spinn magnetisk øyeblikk, eksempler

Det blir bedt om å beregne med disse dataene:

a) Størrelsen på skjærspenningen

b) enhetlig deformasjon Δ

c) Verdien av skjæringsmodulen

Løsning på

Størrelsen på skjærspenningen er:

τ = f/a

Med:

A = side² = (30 x 10^-2 cm)² = 0.09 m²

Derfor:

τ = 1 n / 0.09 m² = 11.1 Pa

Løsning b

UNITURE deformasjon er ingen ringere enn verdien av Δ, gitt av:

Δ = Δx / l

Forskyvningen av ansiktet utsatt for styrken er 1 cm, da:

Δ = 1/30 = 0.0333

Løsning c

Kuttemodulen og kvotienten mellom skjæreinnsatsen og enhetsdeformasjonen:

G = Cutting/Deformation -innsats

Derfor:

G = 11.1 PA /0.033 = 336.4 Pa

Referanser

1. Øl, f. 2010. Materialmekanikk. McGraw Hill. 5. plass. Utgave.
2. Franco Garcia, til. Stivt faststoff. Hør modulmåling. Hentet fra: SC.Ehu.er.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. University of Valladolid. Department of Physics of Condensed Matter. Utvalg av problemer. Gjenopprettet fra: www4.drue.er.