Hva er det statistiske området? (Med eksempler)

Han område, Tur eller amplitude, i statistikk, er forskjellen (subtraksjon) mellom maksimal verdi og minimumsverdien til et sett med data fra en prøve eller en populasjon. Hvis området med bokstaven R og dataene er representert ved hjelp av x, Formelen for serien er ganske enkelt:

R = x_Maks - x_min

 Hvor x_Maks Det er maksimal verdi av dataene og x_min Det er minimum.

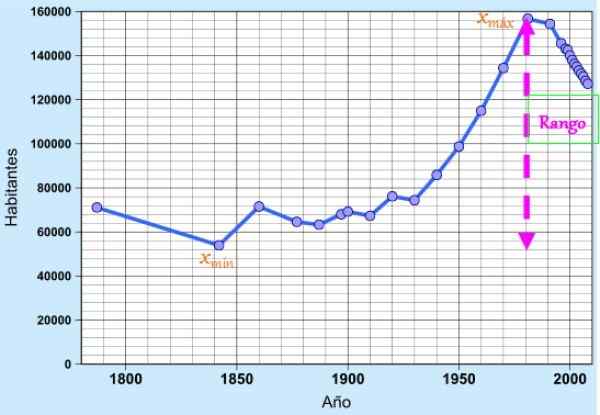
Figur 1. Dataområde som tilsvarer befolkningen i Cádiz de siste to århundrene. Kilde: Wikimedia Commons.

Konseptet er veldig nyttig som et enkelt spredningstiltak for raskt å sette pris på variasjonen i dataene, da det indikerer utvidelsen eller lengden på intervallet der disse er funnet.

Anta for eksempel at en gruppe av 25 mannlige studenter fra det første ingeniøråret ved et universitet. Den høyeste studenten i gruppen måler 1.93 m og den laveste 1.67 m. Dette er de ekstreme verdiene for prøvedataene, derfor er ruten for dem:

R = 1.93 - 1.67 m = 0.26 m eller 26 cm.

Status av studentene i denne gruppen er distribuert i hele dette området.

[TOC]

Fordeler og ulemper

Området er, som vi sa før, et mål på hvor spredt er dataene. Et lite område indikerer at dataene er mer eller mindre nær og spredningen er liten. På den annen side er et større område som er en indikasjon på at dataene er mer spredt.

Fordelene med å beregne området er tydelige: det er veldig enkelt og raskt å finne, fordi det er en enkel forskjell.

Den har også de samme enhetene som dataene det fungerer, og konseptet er veldig enkelt å tolke for enhver observatør.

I eksemplet med statiens studenter, hvis rekkevidden hadde vært 5 cm, vil vi si at studentene har samme størrelse. Men med en rekkevidde på 26 cm, antar vi umiddelbart at det i utvalget er studenter av alle mellomstatninger. Gjør denne antagelsen alltid riktig?

Det kan tjene deg: forskjell mellom sirkel og omkrets (med eksempler)

Ulemper med området som et spredningstiltak

Hvis vi ser nøye ut, i vårt utvalg av 25 ingeniørstudenter, er det bare ett av dem som måler 1.93 og de resterende 24 har staturer nær 1.67 m.

Og likevel forblir rekkevidden det samme, selv om det er helt mulig at det motsatte skjer: at staturen til flertallet svinger rundt 1.90 m og bare en måler 1.67 m.

I alle fall er fordelingen av dataene veldig forskjellig.

Ulempene med området som spredningstiltak skyldes det faktum at det bare bruker ekstreme verdier og ignorerer alle de andre. Ettersom det meste av informasjonen går tapt, er det ingen anelse om hvordan eksempeldataene distribueres.

En annen viktig funksjon er at utvalget av prøven aldri avtar. Hvis vi legger til mer informasjon, det vil si at vi vurderer mer data, øker eller forblir det samme.

Og i alle fall er det nyttig bare når du arbeider med små prøver, anbefales den unike bruken som et mål på spredning i store prøver.

Det som må gjøres er å utfylle beregningen av andre spredningstiltak som tar hensyn til informasjonen gitt av totaldata: rute Interquartilic, Varians, standardavvik og variasjonskoeffisient.

Interkviril rute, kvartiler og løst eksempel

Vi har innsett at svakheten i området som et spredningstiltak er at det bare benytter seg av de ekstreme verdiene for fordelingen av dataene, og utelater de andre.

For å unngå denne ulempen, kvartiler: tre verdier kjent som posisjonstiltak.

De distribuerer dataene som ikke er gruppert i fire deler (andre mye brukte posisjonstiltak er Deciles og Prosentiler). Dette er dens egenskaper:

-Den første kvartilen q₁ Det er verdien av dataene slik at 25 % av dem alle er mindre enn Q₁.

Kan tjene deg: proporsjonalitetskonstant: hva er, beregning, øvelser

-Den andre kvartilen q₂ Det er den median av distribusjonen, noe som betyr at halvparten (50 %) av dataene er mindre enn den verdien.

-Endelig den tredje kvartilen Q₃ påpeker at 75 % av dataene er mindre enn q₃.

Deretter er den interkvotile området eller interkvartilruten definert som forskjellen mellom den tredje kvartilen q₃ Og den første kvartilen q₁ av dataene:

Interquotile Journey = R_Q = Q₃ - Q₁

På denne måten verdien av rangering r_Q Det er ikke så påvirket av ekstreme verdier. Derfor anbefales det å bruke det når det gjelder partiske distribusjoner, for eksempel veldig høye eller veldig lave studenter beskrevet ovenfor.

- Cuartyles beregning

Det er flere måter å beregne dem på, her vil vi foreslå en, men i alle fall er det nødvendig å vite Antall bestilling “N_enten”, Som er stedet som opptar den respektive kvartilen i distribusjonen.

Det vil si hvis for eksempel begrepet tilsvarer q₁ er den andre, tredje eller fjerde og så på distribusjonen.

Første kvartil

N_enten (Q₁) = (N+1) / 4

Andre kvartil eller median

N_enten (Q₂) = (N+1) / 2

Tredje kvartil

N_enten (Q₃) = 3 (n+1) / 4

Hvor n er datatummeret.

Medianen er verdien som er rett midt i distribusjonen. Hvis datanummeret er rart, er det ikke noe problem å finne det, men hvis det er jevnt, er de to sentrale verdiene i gjennomsnitt for å gjøre dem om til en.

Når ordrenummeret er beregnet, følges en av disse tre reglene:

-Hvis du ikke har desimaler, blir dataene som er angitt i distribusjonen søkt, og dette vil være den fjerde søkte.

-Når ordrenummeret er halvveis mellom to, er dataene som er angitt med hele delen av følgende faktum, i gjennomsnitt, og resultatet er den tilsvarende kvartilen.

-I alle andre tilfeller er det nærmeste heltallet avrundet, og det vil være fjerdeplassen.

Kan tjene deg: Additive Principle

Løst eksempel

På en skala fra 0 til 20, en gruppe på 16 matematikkstudenter fikk jeg følgende karakterer (poeng) i en delvis eksamen:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Finne:

a) Data- eller dataruten.

b) Verdiene på kvartilene q₁ og q₃

c) Interquartil -området.

Figur 2. Gjør kvalifikasjonene til denne matematikkundersøkelsen så mye variabilitet? Kilde: Pixabay.

Løsning på

Den første tingen å gjøre for å finne ruten er å bestille dataene øker eller synker. For eksempel i økende rekkefølge har du:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Gjennom formelen gitt i begynnelsen: r = x_Maks - x_min

R = 20 - 1 poeng = 19 poeng.

I følge resultatet har disse karakterene en stor spredning.

Løsning b

N = 16

N_enten (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Det er et tall med desimaler, hvis hele delen er 4. Så går vi til distribusjonen, dataene som inntar fjerdeplassen blir søkt og verdien er i gjennomsnitt med den for femte plassering. Ettersom begge er 9, er gjennomsnittet også 9 og deretter:

Q₁ = 9

Nå gjentar vi prosedyren for å finne Q₃:

N_enten (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Igjen er det en desimal, men siden den ikke er halvveis er den avrundet til 13. Den etterspurte kvartilen inntar tretten stilling og er:

Q₃ = 16

Løsning c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 poeng.

At som vi ser er mye mindre enn dataområdet beregnet i avsnitt A), fordi minimumsvurderingen var 1 poeng, en verdi mye lenger fra resten.

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
4. Eksempler på kvartiler. Hentet fra: Matematikk10.nett.
5. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
6. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.