Hva er forholdet mellom Rhombus og rektangelområdet?

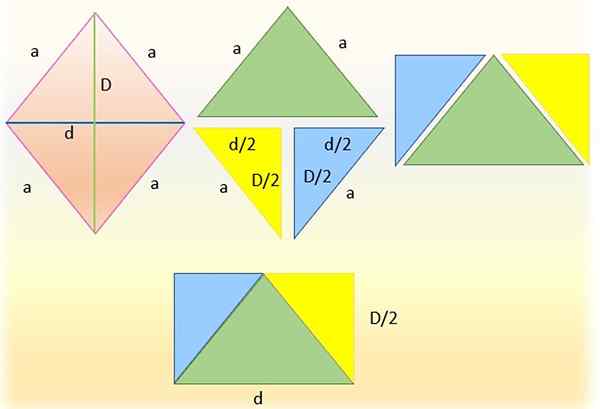
Nedbryter en rhombus for å få et rektangel. Kilde: f. Zapata

Det er mulig å beregne Rhombus -området (og noen andre geometriske figurer) fra området til en trekant eller en beslektet firkantet, for eksempel et parallellogram eller et rektangel.

Rektangelet og parallellogramområdet er det samme: det beregnes som produktet mellom basen av figuren og dens høyde med hensyn til den basen. For sin del er trekantområdet halvproduktet mellom basen og høyden.

Disse formlene er enkle å huske, selv om geometri naturlig gir en eksklusiv formel for Rhombus -området, og vet målet på dets viktigste og mindre diagonaler, betegnet som henholdsvis d og d:

Det er mulig å utlede dette uttrykket gjennom sekvensen vist på figuren over.

For å gjøre dette blir rhombus til venstre kuttet av en av diagonalene, som ble laget i figuren som seksjoner av den mindre diagonalen, og oppnådde dermed to trekanter. Den øvre trekanten (i grønt) er igjen og den nedre er delt i sving til to trekanter, kutt i halvparten av den store diagonalen, og oppnår trekantene rektangler identisk blå og gul.

Da er hypotenusene til disse trekantene sammenfallende med sidene av den grønne trekanten, siden de måler det samme, det vil si "A". Og det oppnås endelig et rektangel, hvis base er den nedre "D" -diagonalen og hvis høyde er halvparten av den viktigste diagonalen, det vil si: "d/2".

Rektangelområdet som det er dannet sammenfaller akkurat det av Rhombus, derfor kan det bekreftes at:

Kan tjene deg: trinomial

TIL _diamant = (base × høyde) _rektangel = D × (d/2)

Et resultat som, som det kan sees, sammenfaller nøyaktig med formelen til Rhombus -området gitt før.

Rombo og parallellogramområdet

Rhombusområdet er også relatert til et parallellogram, siden begge geometriske figurer er flate og tilhører familien til firkantede. I det følgende bildet er det for eksempel en rhombus til venstre og et parallellogram til høyre.

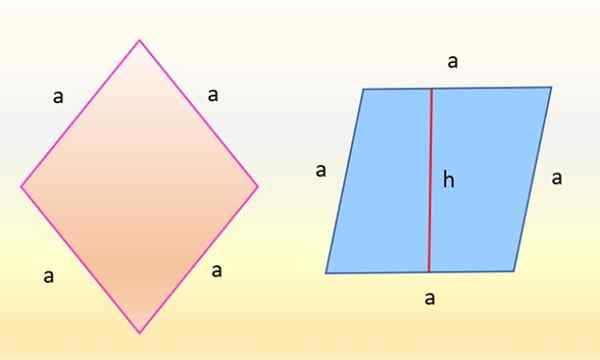Rhombusområdet til venstre er det samme som parallellogrammet til høyre. Kilde: f. Zapata

Det viser seg at tallene er identiske, fordi det som har endret seg bare er orienteringen. Rhombus til venstre, i rosa, hvis sider har samme tiltak: a, er det snudd på en slik måte at en av sidene er helt horisontal. Deretter tar Rhombus formen til det blå parallellogrammet til høyre.

Og området til dette parallellogrammet er også produktet mellom basen "A" og høyden med hensyn til den basen, kalt "H" i figuren, derfor:

TIL _{parallellogram} = En × h

Siden det er den samme figuren, er området identisk og følger det:

TIL _diamant = En × h

Dermed beregnes kunnskap og H for parallellogrammet, og det vil sammenfalle med dets rhombus.

Rombo -området påskrevet i et rektangel

Nok et forhold mellom rhombus og rektangel vises når den første er registrert i det andre. Hvis dette skjer, sammenfaller toppunktene til Rhombus med midtpunktet på sidene av rektangelet, som vises nedenfor:

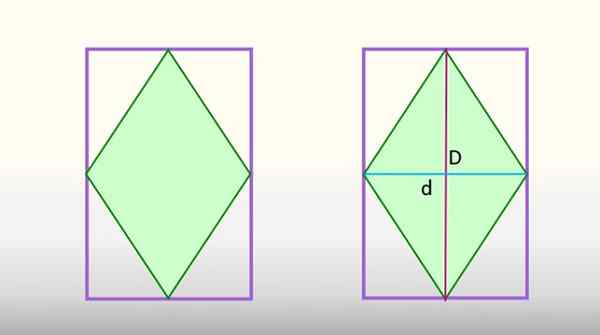Rhombusområdet som er innskrevet i rektangelet tilsvarer halvparten av rektangelområdet. Kilde: f. Zapata

Denne bestemmelsen gjør at de viktigste og mindre diagonalene til Rhombus, figuren er delt inn i 8 identiske trekanter, hvorav 4 tilsvarer Rhombus, i grønt, og de andre 4 er en del av rektangelet. Hvis disse siste 4 trekantene går sammen, ville de danne halvparten av rektangelet, og de 4 rhombus -trekantene, den andre.

Det kan tjene deg: Isosceles Triangle

Derfor tilsvarer Rhombus -området halvparten av rektangelområdet det er registrert, og sier at:

TIL_diamant = A_rektangel / 2

Dette verifiseres enkelt ved å beregne området til en av trekantene og multiplisere med 4, siden de er identiske. Området til en hvilken som helst trekant er halvparten av produktet mellom base og høyden:

TIL _triangel = base × høyde /2

Fra forrige figur observeres det at basen til en av trekantene er d/2 og høyden er d/2, som erstatter i forrige formel gir:

TIL _triangel = (d /2) × (d /2) /2 = (d × d) /8

Multipliser dette resultatet med 4 for å ha Rhombus -området:

TIL _diamant = 4 (d × d) /8 = (d × d) /2

For sin del er halvparten av rektangelet:

TIL _rektangel / 2 = base × høyde / 2

Siden basen til rektangelet er d og høyden er d, gjenstår den:

TIL_rektangel / 2 = d × d/ 2

Som er nettopp området til den registrerte rhombus. Det konkluderes da med at:

Området til en rhombus registrert i et rektangel tilsvarer halvparten av dette området med dette.

Løste øvelser

Oppgave 1

Hvor mye er Rhombus -området hvis store diagonale tiltak 14.6 cm og nedre diagonal 9.8 cm?

Løsning

Ved å erstatte d = 14.6 cm og d = 9.8 cm i Rhombus -områdeformelen:

Det ettertraktede området er:

TIL _diamant = 14.6 cm × 9.8 cm = 143.1 cm²

Oppgave 2

I figuren av den foregående delen, måler den viktigste diagonalen til rhombus som er registrert i rektangelet d = 30 cm og rektangelområdet er verdt 210 cm². Det blir bedt om å beregne:

a) lengden på den mindre diagonalen

Det kan tjene deg: Linje og semi -AVIVER -segment

b) Rhombus -området, på to måter: det første gjennom rektangelområdet og det andre ved å bruke formelen til området til en rhombus. Sjekk at resultatet er det samme.

Løsning på

Rektangelområdet er produktet mellom basen og høyden. Den største diagonalen er høyden, mens den minste diagonalen d ville være basen. Ved å bruke arealformelen og erstatte verdiene til uttalelsen, har du:

TIL _rektangel = base × høyde = d × 30 cm = 210 cm²

Da er basen verdt:

D = 210 cm² / 30 cm = 7 cm

Løsning b

Som sett over, er Rhombus -området halvparten av rektangelområdet, og dette er kjent:

TIL _diamant = 210 cm² /2 = 105 cm²

Resultatet blir sjekket umiddelbart, erstattet i formelen:

Diagonalene er allerede kjent: D = 30 cm, d = 7 cm, deretter:

TIL _diamant = 30 cm × 7 cm /2 = 105 cm²

Det er bevist at Rhombusområdet som forventet er det samme i begge tilfeller.