Kvadratrot av 3 (enkel løsning og forklaring)

Square Root of 3 er 1.73205080756887.

Det kan uttrykkes:

√3 = 1.73205080756887

Å vite hva som er 3 kvadratrot, Det er viktig å vite definisjonen av kvadratroten til et tall. Gitt et positivt tall "A", er kvadratroten til "A", betegnet med √a, et positivt tall "B" slik at når "B" multipliseres med det, er resultatet "A".

Den matematiske definisjonen sier: √a = b Ja, og bare hvis, b² = b*b = a. Derfor, for å vite hva som er kvadratroten til 3, det vil si verdien av √3, må et "B" -tall bli funnet at b² = b*b = √3.

I tillegg er √3 et irrasjonelt tall, som består av en uendelig ikke -periodisk mengde desimaler. Av denne grunn er det vanskelig å beregne kvadratroten til 3 manuelt.

3 kvadratrot

Hvis en kalkulator brukes, kan det sees at kvadratroten til 3 er 1.73205080756887 ..

Nå kan du manuelt prøve å tilnærme dette tallet som følger:

-1*1 = 1 og 2*2 = 4, sier dette at kvadratroten til 3 er et tall mellom 1 og 2.

-1,7*1,7 = 2,89 og 1,8*1,8 = 3,24, derfor er den første desimaltallet 7.

-1,73*1,73 = 2,99 og 1,74*1,74 = 3,02, og det andre desimalet er 3.

-1.732*1 732 = 2,99 og 1 733*1 733 = 3,003, derfor er det tredje desimalet 2 2.

Og så videre kan du fortsette. Dette er en manuell måte å beregne kvadratroten til 3.

Det er også andre mye mer avanserte teknikker, for eksempel Newton-Raphson-metoden, som er en numerisk metode for å beregne tilnærminger.

Hvor kan vi finne tallet √3?

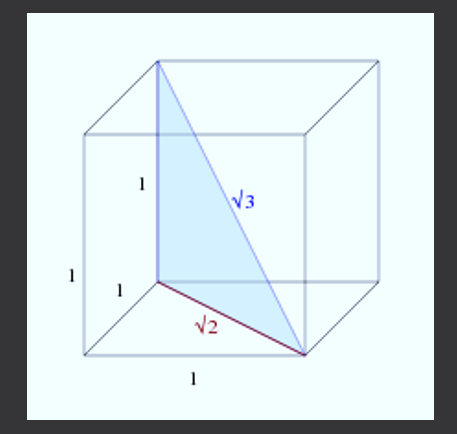
På grunn av det kompliserte antallet, kan det tenkes at det ikke vises i hverdagsobjekter, men dette er usant. Hvis du har en kube (firkantet boks), slik at lengden på sidene er 1, vil kubediagonalene ha et mål på √3.

For å bekrefte dette brukes Pythagoras -teoremet som sier: gi.

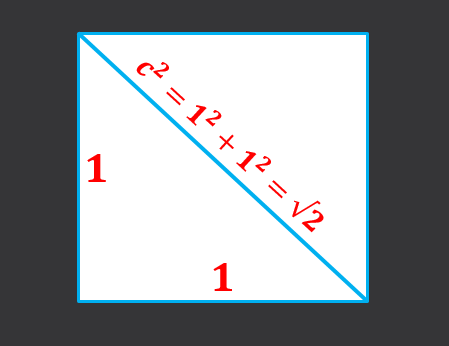
Å ha en side av side 1, må du diagonal av kvadratet på basen er lik summen av rutene til kategoriene, det vil si C² = 1²+1² = 2, derfor diagonalen til basismålet √2.

For å beregne kubediagonalen kan du se følgende figur.

Den nye rektangeletrekanten har ben med lengde 1 og √2, derfor når du bruker Pythagoras -teoremet for å beregne lengden på dets diagonale, oppnås: C² = 1²+(√2) ² = 1+2 = 3, sier det , C = √3.

Dermed er lengden på diagonalen til en sidebøtte 1 lik √3.

√3 Et irrasjonelt tall

I begynnelsen ble det sagt at √3 er et irrasjonelt tall. For å bekrefte dette antas det av absurditeten som er et rasjonelt tall, som det er to tall "A" og "B", relative søskenbarn, for eksempel A/B = √3.

Når den siste likheten og klare “A²”, oppnås følgende ligning: A² = 3*B². Dette sier at "A²" er et multiplum av 3, som konkluderer med at "A" er et multiplum av 3.

Å være "et" multiplum av 3, det er et heltall "k" slik at a = 3*k. Derfor oppnås det ved å erstatte i den andre ligningen: (3*k) ² = 9*k² = 3*B², som er det samme som B² = 3*K².

Som før fører denne siste likheten til konklusjonen at "B" er et multiplum av 3.

Avslutningsvis er "A" og "B" begge multipler av 3, noe som er en motsetning, fordi det til å begynne med ble antatt at de var relative søskenbarn.

Derfor er √3 et irrasjonelt tall.