Trigonometriske grunner til eksempler, øvelser og applikasjoner

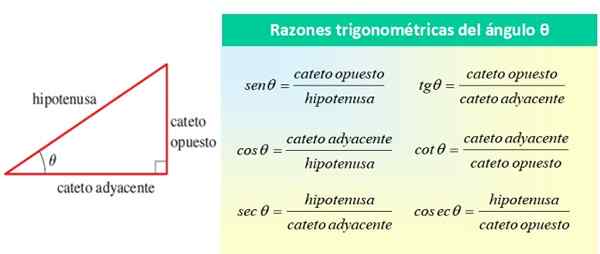
De trigonometriske grunner De er kvotientene eller årsakene som kan gjøres med verdien av sidene av en høyre trekant. Disse sidene er: to kategorier som danner 90º med hverandre og hypotenusen, som danner den akutte vinkelen θ med en av kategoriene.

6 kvotienter kan dannes. Deres navn og respektive forkortelser er:

• BREACE (SEN)
• Coseno (cos)
• Tangent (TG eller Tan)
• Cotangent (CTG eller Cotan)
• Secante (sek) og
• Harvester (Harmony)

Alle refererte til vinkel θ, som vist i følgende figur:

Figur 1. De trigonometriske årsakene til den akutte vinkelen θ. Kilde: f. Zapata.

De grunnleggende trigonometriske årsakene til vinkel θ er sin θ, cos θ og tan θ, mens de gjenværende årsakene kan uttrykkes i form av disse tre. Fra forrige bilde kan du se det:

• Sek θ = 1/ cos θ
• skade θ = 1/ sin θ
• barneseng θ = 1/tg θ

Størrelsen på trekantens sider påvirker ikke verdien av årsakene, siden to trekanter hvis vinkler måler de samme er lignende trekanter og de respektive kvotientene mellom sidene har samme verdi.

[TOC]

Eksempel

La oss for eksempel beregne de trigonometriske årsakene til vinkelen θ i følgende trekanter:

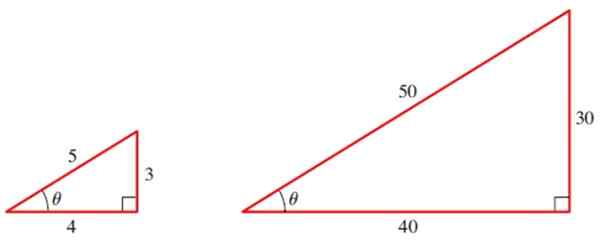Figur 2. To lignende trekanter har de samme trigonometriske årsakene til vinklene sine. Kilde: Stewart, J.Preccculment: Matematikk for beregning.

For den lille trekanten har vi de tre grunnleggende årsakene til vinkelen θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

Og la oss nå beregne de tre grunnleggende årsakene til θ med den store trekanten:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

En viktig detalj å vurdere er som følger: både sin θ og cos θ er mindre enn 1, siden kategoriene alltid måler mindre enn hypotenusen. Faktisk:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Løste øvelser

I de følgende øvelsene blir det bedt om å løse riktig trekant, som betyr å finne lengden på de tre sider og målet på dens indre vinkler, hvorav den ene alltid måler 90º.

Kan tjene deg: Først -grads ligninger: Formel, hvordan du løser dem, eksempel, øvelser

Pythagoras teorem gjelder rektangeltrekanter og er veldig nyttig når to av sidene er kjent og de mangler må bestemmes. Teoremet sier:

Hypotenuse² = motsatt kateto² + tilstøtende kateto²

Vi kan bekrefte Pythagoras -teoremet med den lille trekanten i figur 2, hvis ben er 3 og 4. Rekkefølgen som kategoriene er tatt, spiller ingen rolle. Bruke teoremet vi har:

Hypotenuse² = 3² + 4² = 9 + 16 = 25

Derfor er hypotenusen:

Hypotenuse = √25 = 5

- Oppgave 1

Beregn de trigonometriske årsakene til vinklene som er vist i følgende trekanter:

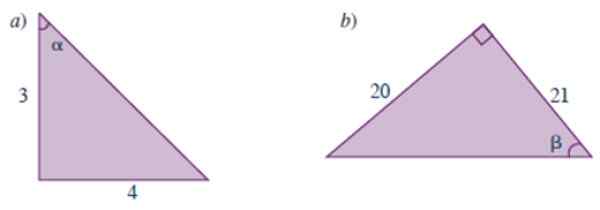Figur 3.- Trekanter for året løst 1. Kilde: Carena, M. 2019. Preuniversity Mathematics Manual.

Løsning på

Denne trekanten er den samme i figur 3, men de ber oss om de trigonometriske årsakene til den andre akutte vinkelen, betegnet α. Uttalelsen tilbyr ikke verdien av hypotenusa, men ved anvendelse av Pythagoras -teoremet vet vi at det er verdt 5.

Årsakene kan beregnes direkte fra definisjonen, og vær forsiktig når du velger benet som er det motsatte av vinkelen α for å beregne sen α. La oss se:

• sin α = 4/5
• cos α = 3/5
• TG α = 4/3
• barneseng α = ¾
• SEC α = 1/(3/5) = 5/3
• skade α = 1/(4/5) = 5/4

Og som vi kan se, er verdiene til trigonometriske grunner blitt utvekslet. Faktisk er α og θ komplementære vinkler, noe som betyr at de tilsetter 90º. I dette tilfellet blir det oppfylt at sen α = cos θ og så videre av de andre grunnene.

Løsning b

La oss beregne hypotenusen til trekanten gjennom Pythagoras teorem:

Hypotenuse² = 20² + tjueen² = 841

√841 = 29

Da er de 6 trigonometriske årsakene til vinkel β:

• Sen β = 20/29
• cos β = 21/29
• TG β = 20/21
• Barneseng β = 21/20
• SEC β = 1/(21/29) = 29/21
• skade β = 1/(20/29) = 20/29

Kan tjene deg: kombinert operasjoner

- Oppgave 2

a) Finn verdien av x i figuren.

b) Beregn omkretsen til de 3 viste trekantene.

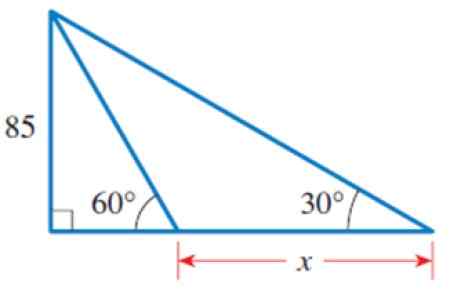Figur 4. Trekanter for året løst 2. Kilde: Stewart, J. Preccculment: Matematikk for beregning.

Løsning på

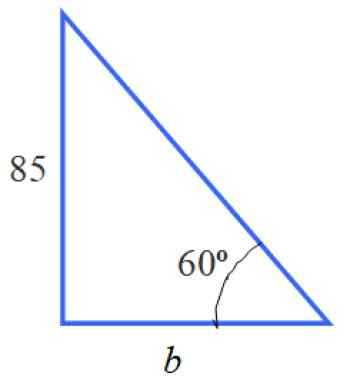
I figuren kan vi identifisere flere trekanter, spesielt rektangelets trekant av venstre, som har en kategori lik 85 og den akutte vinkelen 60º.

Figur 5. Trekanten til venstre.

Med informasjonen om denne trekanten kan vi beregne side B. Det er ikke tiltaket at uttalelsen spør, men å vite verdien er et tidligere trinn.

For å bestemme den aktuelle årsaken er Tg 60 º = 85 /B, siden B er beinet ved siden av 60 ° og 85 er motsatt av nevnte vinkel. Derfor:

B = 85 / Tg 60º = 85 / √3

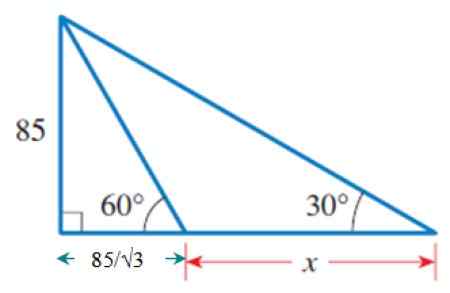
Når vi er kjent B, vil vi bruke den store og ytre rektangel -trekanten, som har en felles side med den forrige trekanten: den som måler 85. Dette er katetoet i motsetning til vinkelen på 30º.

Figur 6. Den ytre trekanten, hvorav en del av basen allerede er kjent.

Derfra:

Kateto ved siden av 30º = (85/√3) + x

Nå kan vi heve følgende:

85 / [(85 / √3) + x] = Tg 30º

Hva er i firkantede parenteser multipliserer 30 º tg:

85 = [(85/√3) + x]. TG 30º

Bruke distribusjonsegenskapen til multiplikasjon:

85 = Tg 30º. (85/√3) + x. TG 30º

Derfor:

x.Tg 30º = 85 - Tg 30º. (85/√3) = 85 [1 - Tg 30º . (1/√3)] = 85 . (2/3) = 170/3

Bytte ut Tg -verdien 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.femten

Løsning b

Omkretsen av den lille trekanten

Være h₁ Hypotenusen til denne trekanten, som kan beregnes av Pythagoras teorem eller gjennom en trigonometrisk grunn, for eksempel COS 60º:

cos 60 º = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60º = 98.1

For å finne P, omkretsen av denne trekanten, legger vi ganske enkelt til de 3 sidene:

Kan tjene deg: Beskrivende statistikk: Historie, egenskaper, eksempler, konsepter

P = 85 + (85/√3) + 98.1 = 232.2

Omkretsen av den ytre trekanten

Være h₂ til hypotenusen til den ytre trekanten:

Sen 30º = 85 ÷ h₂  

h₂ = 85 ÷ sin 30º = 170

For denne trekanten er omkretsen:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Omkretsen av ikke -rectangle -trekanten

Fra denne trekanten kjenner vi allerede alle sidene:

P = x + h₁ + h₂ = 98.15 + 98.15 + 170 = 366.3

Bruksområder av trigonometriske grunner

Trigonometriske grunner har mange praktiske anvendelser, for eksempel høyder kan beregnes.

Anta at et vanntårn er 325 fot fra en bygning. En observatør som ligger i et vindu, merk at høydevinkelen på den øvre enden av tårnet er 39 º, mens depresjonsvinkelen som tårnets base er 25º. Underverker:

a) Hva er høyden på tårnet?

b) Hvor mye er vinduet?

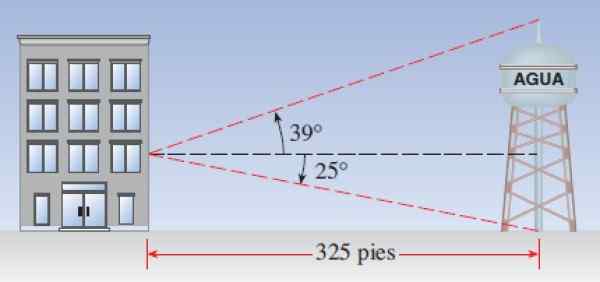Figur 7. Ordning for å beregne høyden på Vista Torre fra en bygning. Kilde: Stewart, J. Preccculment: Matematikk for beregning.

Løsning på

Fra kateto motsatt til 39 av øvre trekant får vi en del av svaret:

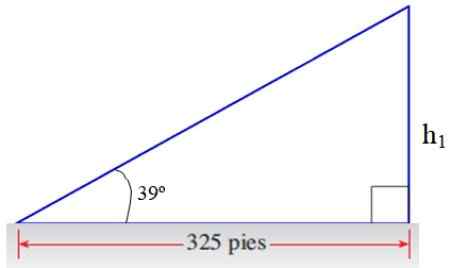Figur 8. Trekant for søknadsøvelse. Kilde: f. Zapata.

h₁/325 = Tg 39º → H₁ = 325 . TG 39º fot = 263.2 fot

På lignende måte får vi resten av høyden på tårnet, kalt h₂ Fra nedre trekant:

h₂/325 = Tg 25º → H₂ = 325 . Tg 25º fot = 151.6 fot

Den totale høyden på tårnet er h₁ + h₂ = 263.2 + 151.6 fot = 414.7 fot.

Løsning b

Vinduet er nettopp i en høyde h₂ bakke:

h₂ = 151.6 fot.

Referanser

1. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
2. Hoffman, J. Valg av matematikkproblemer. Volum 3.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.