Område av en vanlig og uregelmessig Pentagon hvordan det tas, øvelser

Å beregne område av en femkant Først må vi avgjøre om dette er regelmessig eller ikke er. En Pentagon er en polygon, en lukket flat figur på fem sider. Når en polygon er vanlig, betyr det at lengden på sidene er den samme og dens indre vinkler også.

I så fall er det en formel for å beregne det nøyaktige området til den vanlige polygonen, og kjenne til noen av hovedegenskapene, som vi vil utlede senere.

To pentagoner

Hvis polygonen ikke er regelmessig, det vil si at den har sider av forskjellige størrelser og ulik indre vinkler, er det ingen enkelt formel.

Imidlertid har matematikere funnet beregningsstrategier, for eksempel å dele figuren i andre med det laveste antall sider, for eksempel trekanter, firkanter og rektangler, hvis dimensjoner er kjent eller lett beregnet.

En annen prosedyre for å beregne områder med polygoner generelt, og kjenne koordinatene til toppunktene, er metoden som heter Gauss Determinants, som vi vil beskrive senere.

[TOC]

Hvordan beregne området til en vanlig Pentagon?

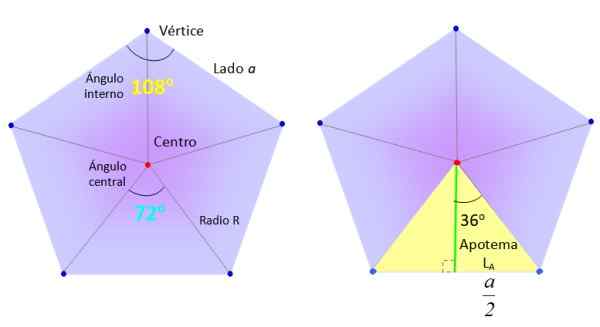
Vi kommer til å ta en vanlig Pentagon fra side A, og vi vil dele den inn i 5 like trekanter som vist på figuren og tegne segmenter fra sentrum (rødt) til toppunktene (blå).

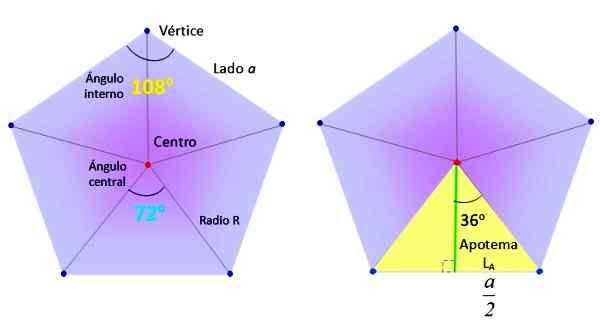De nødvendige elementene for å finne det vanlige Pentagon -området. Kilde: f. Zapata.

På sin side er trekantene, som den enestående gule til høyre i den øvre figuren, delt inn i to like rektangler, takket være det grønne segmentet, kalt Apothem.

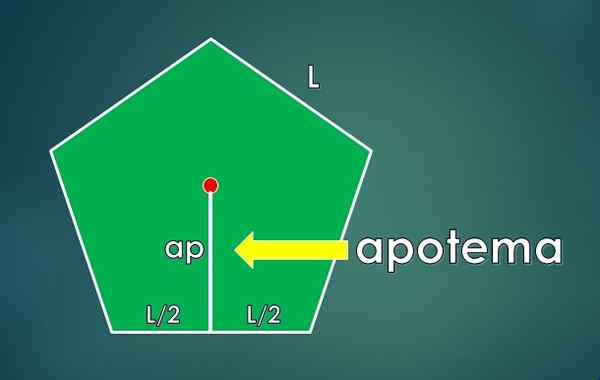
Apotheme er definert som det vinkelrett segmentet som kobles til midten av polygonen med midten av den ene siden. Lengden er l_TIL.

Området med et rektangel trekant av base a/2 og høyde l_TIL er:

[(A/2) x l_TIL]

Pentagon har 10 trekanter som dette, derfor er området:

Kan tjene deg: vektorfunksjoner

A = 10 (a/2) x l_TIL

Men omkretsen P av Pentagon er nøyaktig p =10a, Derfor er området gitt av semi -produkten av omkretsen og apothemets lengde:

A = p x l_TIL /2

Vanlig Pentagon -område å kjenne siden a

Uttrykke lengden på apothem l_TIL Avhengig av side A, vel vitende om at den indikerte vinkelen er halvparten av den sentrale vinkelen, er det 36 º, tilsvarer:

36º = π/5

Av Elementary Trigonometry, ved tangent av den akutte vinkelen 36º:

Tan (π/5) = (a/2) ÷ l_TIL

Derfor:

L_TIL=  (A/2) ÷ solbrun (π/5)

Erstatning i området trukket i forrige seksjon, og vite at p = 5a:

A = p x l_TIL /2

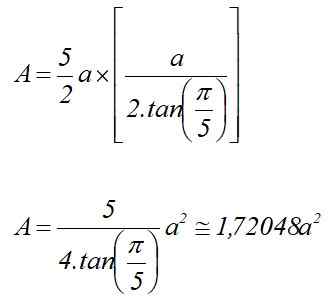
Vanlig Pentagon -område som kjenner radioen

Han radio av en vanlig polygon er segmentet som går fra sentrum til en av sine hjørner. Den sammenfaller med radius for den omskrevne omkretsen, som vist i følgende figur:

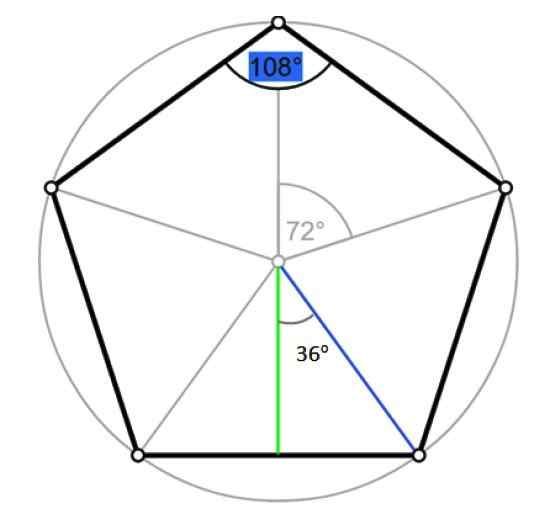Vinkler og apothem av femkant. Kilde: Wikimedia Commons/F. Zapata.

La R være målet for nevnte radio, som sammenfaller med hypotenusen til høyre trekant avgrenset i forrige figur, i blått. Av trigonometri:

cos 36º = cos (π/5) = l_TIL ÷ r

OG

sin 36º = sin (π/5) = (a/2) ÷ r

Derfor:

A = p x l_TIL /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Bruke dobbeltvinkelformelen:

sin (2θ) = 2 sen θ . cos θ

Vi må:

[sin (π/5) x cos (π/5)] = (1/2) SIN 72º

Og ved å erstatte denne verdien, oppnår vi følgende formel for det vanlige Pentagon -området:

A = (5/2) r².Sen 72º

Hvordan beregne området til en uregelmessig femkant?

Som vi har sagt før, for en uregelmessig polygon er det ingen enkelt formel, men det er to metoder som vanligvis fungerer veldig bra, den første kalles triangulering og den andre er metoden for Gauss Determinants.

Kan tjene deg: eksistens og unikhet teorem: demonstrasjon, eksempler og øvelser

Triangulering

Den består av å dele figuren i trekanter, hvis område er lettere å beregne, eller også kan testes med andre figurer hvis område er kjent, for eksempel firkanter, rektangler og trapesider.

Gauss Determinants

En annen måte å finne det uregelmessige Pentagon -området eller annen uregelmessig polygon er å plassere figuren i et kartesisk koordinatsystem, for å finne koordinatene til toppunktene.

Gauss Determinants -metoden er kjent for å beregne området, som er gitt med følgende formel:

Hvor a er området til polygon og (x_n , og_n ) er koordinatene til toppunktene. En polygon av N -sider har 5 hjørner, for Pentagon ville det være n = 5:

Stengene som følger med formelen er modulstenger eller absolutt verdi.

Dette betyr at selv om resultatet av operasjonen er negativt, må vi uttrykke det med et positivt tegn, og hvis den allerede er positiv, må det sitte igjen med det tegnet. Dette er fordi et område alltid er en positiv mengde.

Prosedyren kalles Gauss Determinants av sin skaper, den tyske matematikeren Carl F. Gauss (1777-1855). De indikerte operasjonene tilsvarer determinanten for en 2 × 2 -matrise, for eksempel er den første determinanten:

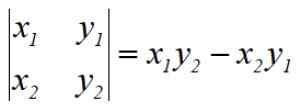
For å finne Pentagon -området vi må løse 5 determinanter, legg til resultatet algebraisk, del det med 2 og til slutt uttrykke området alltid med et positivt tegn.

Løste øvelser

Oppgave 1

Finn det vanlige Pentagon -området hvis Apothem er verdt 4 cm og hvis side måler 5.9 cm.

Løsning

Siden det er en vanlig Pentagon, og vi har mål på siden og apotemet, bruker vi formelen som er trukket tidligere:

Kan tjene deg: Scaleno Triangle

A = p x l_TIL /2

Operimeter P er lik 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Oppgave 2

Finn det uregelmessige Pentagon -området som er vist. Følgende dimensjoner er kjent:

DC ≈ av

AE = AB = 5

BC = 12

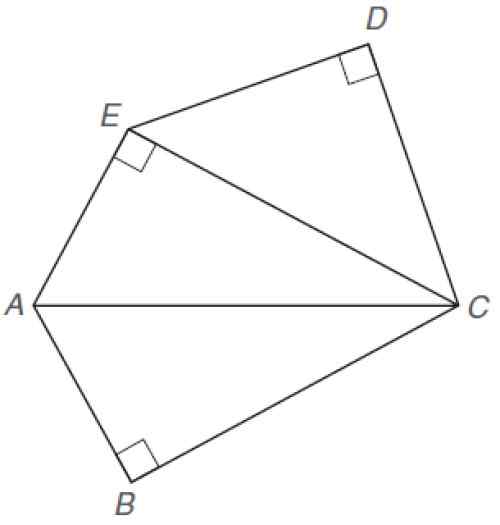Uregelmessig Pentagon. Kilde: Alexander, D. 2013. Geometri. 5. plass. Utgave. Cengage Learning.

Løsning

Pentagon -området er summen av områdene til trekantene, som er rektangler. Uttalelsen sier at DC ≈ av, derfor når du bruker Pythagoras -teoremet til EDC -trekanten, har den:

Ec² = 2 Ed². Da EC = √2.Ed.

AEC og ABC -trekanter har en felles hypotenuse, som er AC -segmentet, derfor:

Ea² + Ec² = Ab² + BC²

Når EA og AB måler det samme, oppnås det at:

EC = BC = √2.Ed

Siden BC = 12, deretter ED = 12 / √2 = 8.485.

Med disse verdiene vil vi beregne området til hver trekant og legge dem til på slutten.

EDC Triangle Area 

Ed x DC /2 = 8.485² / 2 = 36

AEC Triangle Area 

Ea x ec / 2 = ea x √2.ED / 2 = 5 x √2. 8.485/2 = 30

ABC Triangle Area 

AB X BC / 2

Da er området som ble søkt:

5 x 12/2 = 30

Det er det samme som for Triangle AEC, siden begge har de samme tiltakene.

Uregelmessig Pentagon -område

Endelig er det forespurte området summen av områdene til de tre trekantene:

A = 36 + 30 + 30 enheter = 96 enheter.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Matematikk åpen referanse. Polygonområde. Gjenopprettet fra: Mathpenref.com.
3. Universformler. Område av en uregelmessig femkant. Gjenopprettet fra: Universoformulas.com.
4. Universformler. Område av en vanlig femkant. Gjenopprettet fra: Universoformulas.com.
5. Wikipedia. Pentagon. Gjenopprettet fra: er.Wikipedia.com.