Induktiv reaktans

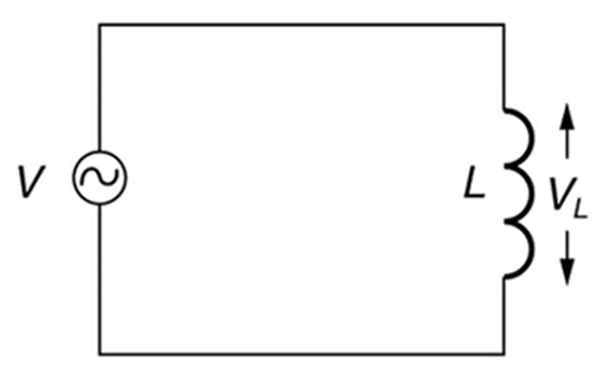
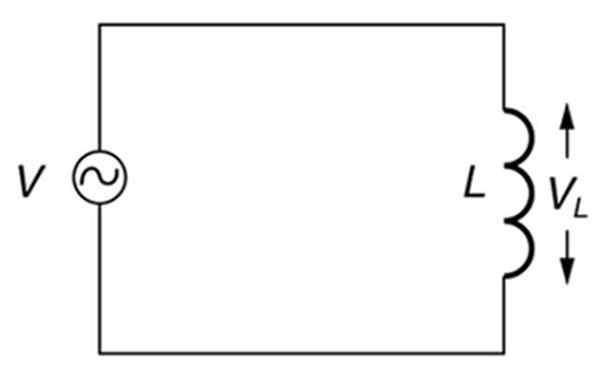En rent induktiv alternativ krets. Kilde: Åpne Stax. College Physics.

Hva er induktiv reaktans?

De Induktiv reaktans Det refererer til opposisjonen presentert av spolen til passering av strømmen, i en alternativ krets. Med andre ord, det er inducerens evne til å redusere strømmen i en alternativ krets. Betegnet som x_L, Verdien avhenger av induktansen og vinkelfrekvensen til spenningen:

X_L= Ω ∙ l

Hvor ω er vinkelfrekvensen i radianer/s og l induktans, målt i Henrios (H) i det internasjonale systemet med enheter hvis.

Store induktanser gir stor induktiv reaktans, siden deres motstand mot endring er større. Og reaktansen øker også med frekvensen, så en viss induktans l vil gi større reaktans, jo høyere er spenningsfrekvensen.

Den induktive reaktansenheten er Ohmio, symbolisert av ω. Det er den samme enheten av elektrisk motstand, men i motsetning til dette, x_L Det er ikke konstant, siden det avhenger av hyppigheten av den påførte alternative spenningen.

Derfor, i en krets hvis eneste elementer er en alternativ kilde og en induktans (induktiv krets), for eksempel den som er vist på figuren over, vil den induktive reaktansen avhenge av frekvensen av kilden.

Xs analogi_L Med elektrisk motstand kan den utvides til den induktive kretsen, og tillater anvendelse av Ohms lov. Hvis x er definert_L som forholdet mellom spenningsamplituder V_L I induktoren, og strømmen i_L som krysser det:

X_L = V_L / Yo_L

Du kan skrive Ohm -loven for rent induktive kretsløp som følger:

V_L = X_L∙ Jeg_L

Induktive reaktansformler

For å beregne den induktive reaktansen brukes formelen som er gitt i begynnelsen, der L representerer induktans (Henrios) og ω er vinkelfrekvensen (radianer/sekund):

Kan tjene deg: Millikan Eksperiment: Prosedyre, forklaring, betydning

X_L= Ω ∙ l

Det er vanlig at frekvensen kommer til uttrykk i Hertz eller Hertzio (HZ). I dette tilfellet er det betegnet med F og er relatert til vinkelfrekvensen gjennom formelen:

Ω = 2π ∙ f

I dette tilfellet beregnes reaktansen som:

X_L= 2πf ∙ l

I noen av disse formlene resulterer den induktive reaktansen i ohm, som tidligere forklart.

Effekten av induktans på en induktiv krets

Fordi induktansen motsetter seg endringene eller variasjonene i strømmen, karakteriseres den induktive reaktansen ved å utsette strømbølgen med hensyn til spenningsbølgen.

I den følgende grafen, som viser spenning V_L (Blå) og strømmen i_L (rød) I induktoren, begge sinoidalt, observeres det at begge bølger er utdatert 90º. Fra og med t = 0 er spenningsverdien maksimal, men strømmen er null i det øyeblikket.

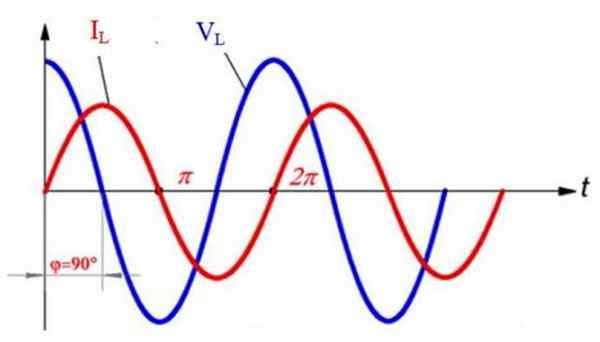Alternativ strøm og spenning i en induktiv krets. Utarbeidet av: f. Zapata.

Senere observeres det at strømmen når sin maksimale verdi ved t = π /2, men da blir spenningen kansellert og investerer sin polaritet, det vil si at den blir negativ. Samtidig reduserer strømmen verdien, mens spenningen blir mer og mer negativ.

Deretter, ved t = π, når spenningen sin maksimale størrelse, selv om den med den omvendte polariteten, og deretter blir strømmen kansellert. Fra alt dette følger det at når V_L Den når en topp, strømmen blir kansellert, og hver gang strømmen når sin maksimale størrelse, er spenningen 0.

Strømmen når alltid toppen etter at spenningen gjør det, og dette skyldes at induktansen i begynnelsen motsetter seg øker eller reduseres.

Kan tjene deg: Mekanisk fordel: Formel, ligninger, beregning og eksempler

Hvordan beregne den induktive reaktansen

Beregning av den induktive reaktansen er veldig enkel: det er nødvendig å vite verdien av induktansen og hyppigheten av den alternative spenningen som er påført. Deretter erstattes disse dataene i en av formlene gitt i foregående avsnitt, og den tilsvarende operasjonen utføres.

Følgende eksempler og løste øvelser viser hvordan du gjør det i forskjellige situasjoner.

Eksempler

Eksempel 1

Anta at a l = 5 MH induktor, som en alternativ frekvensspenning påføres 60.0 Hz. Den induktive reaktansen i dette tilfellet beregnes av:

X_L= 2πf ∙ l

Men før de erstatter verdiene, må induktansen bli Henrios, multiplisere med 1 × 10 -faktoren⁻³. Derfor:

L = 5 × 10⁻³ H

Så:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10⁻³ H = 1. 88 Ohm

Eksempel 2

Nå er den samme induktansen koblet til en annen alternativ frekvensspenning: 10.0 kHz. I dette tilfellet presenterer induktans en større reaktans:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10⁻³ H = 314.2 ohm

Eksempel 3

Spenningen påført induktansen av eksempler 1 og 2 har en verdi på 120 V RMS. Den respektive RMS -strømmen bestemmes gjennom Ohm V -loven_L = X_L∙ Jeg_L:

Yo_L = V_L / X_L

For frekvensen på 60.0 Hz, strømmen er:

Yo_L = 120 V / 1. 88 ohm = 63.8 a

Og for frekvensen på 10.0 kHz:

Yo_L = 120 V / 314.2 ohm = 0.38 a

Siden i sistnevnte tilfelle reaktansen er mye større, forventes det at strømmen vil være mindre. Denne egenskapen gjør induktoren til et høyfrekvensfilter, en funksjon som brukes til å redusere høyfrekvente lyder i lydutstyr, eller for å beskytte enheter mot plutselige nåværende UPS, blant andre applikasjoner.

Kan tjene deg: Steiner Theorem: Forklaring, applikasjoner, øvelser

Løste øvelser

Oppgave 1

Bestem den induktive reaktansen i en krets som består av en induktans på 2.5 MH, i serie med en alternativ spenningskilde, hvis frekvens er 75 r.p.m.

Løsning

En fullstendig revolusjon eller syklus tilsvarer 2π radianer, og et minutt har 60 sekunder, derfor en frekvens på 75 r.p.M tilsvarer:

75 r.p.M = 75 × 2π radianer / 60 sekunder = 7.85 radianer/s

Og med denne verdien er reaktansen:

X_L= Ω ∙ l = (7.85 radianer/s) × 2.5 × 10⁻³ H = 0.02 Ω

Oppgave 2

Seriell induktans brukes med kilden til en datamaskin for å filtrere støyen fra høye frekvenser.

a) Hva som skal være den minste induktansverdien som er nødvendig for å produsere en 2 kΩ reaktans, hvis frekvensen av signalet som skal filtrere er 15 kHz?

b) Finn reaktansen til denne induktoren i frekvensen av 60 Hz.

Løsning på

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Derfor rydding av ligning x_L= 2πf ∙ l, du har:

L = x_L / 2π ∙ F = 2000 Ω / 2π × 15000 Hz = 0.0212 H = 21.2 MH

Løsning b

Bruker x igjen_L= 2πf ∙ L, men med F = 60 Hz, resultater:

X_L= 2π × 60 Hz × 0.0212 H = 8 ohm.

Referanser

1. Bauer, w. (2011). Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 
2. Giancoli, d. (2006). Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
3.  Katz, d. (2013). Fysikk for forskere og ingeniører. Grunnlag og tilkoblinger. Cengage Learning.
4. Åpne Stax. College Physics. Hentet fra: OpenStax.org.
5. Sears, z. (2016). Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2. Pearson