Obliske rettighetskarakteristikker, ligninger og eksempler

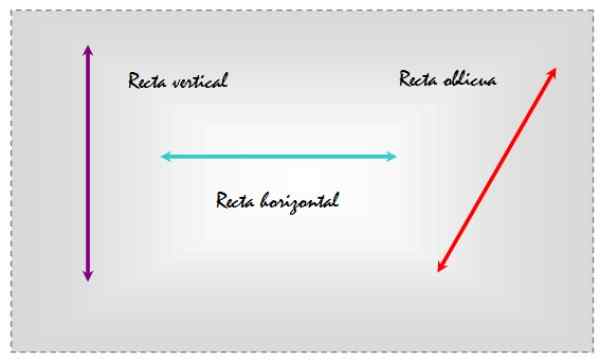
De skrå linjer De er de som er tilbøyelige, enten med hensyn til en flat overflate eller en annen linje som indikerer en bestemt adresse. Vurder som et eksempel de tre linjene tegnet i et fly som vises i følgende figur.

Vi kjenner deres respektive relative posisjoner fordi vi sammenligner dem med en referanselinje, som vanligvis er X akse som betegner det horisontale.

Figur 1. Vertikale, horisontale og skrå linjer i samme plan. Kilde: f. Zapata.

På denne måten, velger den horisontale referansen, er venstre linje vertikal, sentrum er horisontalt og den til høyre er skrå, siden det er skråstilt med hensyn til de daglige referanselinjene.

Nå inntar linjene som er på samme plan, for eksempel overflaten på papiret eller skjermen, forskjellige posisjoner i forhold til hverandre, avhengig av om de krysser eller ikke. I det første tilfellet er de tørre rett, mens de i det andre er parallelle.

På den annen side kan tørkelinjer også være skrå eller vinkelrett rette linjer. I begge tilfeller er linjene på linjene forskjellige, men de skrå linjene dannes seg imellom α og ß -vinklene, annet enn 90º, mens vinklene bestemt av de vinkelrett linjene alltid er 90º.

I den følgende figuren er disse definisjonene oppsummert:

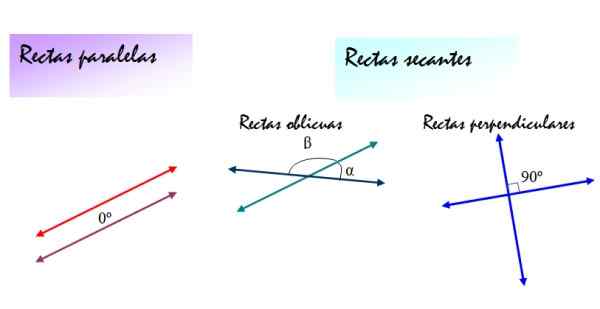Figur 2. Relative posisjoner mellom linjer: parallell, skrå og vinkelrett varierer i vinkelen som dannes med hverandre. Kilde: f. Zapata.

[TOC]

Ligninger

For å kjenne de relative posisjonene til linjene i flyet, er det nødvendig å kjenne vinkelen de dannes med hverandre. Merk at linjene er:

Kan tjene deg: beregning av tilnærminger ved bruk av differensialer

Parallell: Hvis de har samme skråning (like retning) og aldri krysser hverandre, så er poengene deres like store.

Tilfeldigheter: Når alle poengene deres sammenfaller og derfor har samme skråning, men avstanden mellom punktene er null.

Secantes: Hvis øreringene dine er forskjellige, varierer avstanden mellom poengene deres og krysset er et enkelt punkt.

Så en måte å vite om to linjer i flyet er tørre eller parallelle er gjennom skråningen. Kriteriene for parallellisme og vinkelrett på linjene er følgende:

Være to linjer l₁ og jeg₂ tilhører et fly, hvis verserende er henholdsvis m₁ og M₂. Disse linjene er parallelle hvis m₁ = m₂ og de er vinkelrett når m₁= -1/m₂

Hvis det å kjenne bakkene til to linjer i flyet, er ingen av de ovennevnte kriteriene oppfylt, konkluderer vi med at linjene er skrå. Når vi kjenner to punkter på en linje, beregnes skråningen umiddelbart, som vi vil se i neste avsnitt.

Du kan finne ut om to linjer er tørre eller parallelle med tilfeldig.

Dette kriteriet informerer oss imidlertid ikke om vinkelen mellom disse linjene, selv om de har kryss.

For å kjenne vinkelen mellom linjene, er det nødvendig med to vektorer eller og v som tilhører hver av dem. Dermed er det mulig å kjenne vinkelen de danner gjennom skalarproduktet til vektorene, definert på denne måten:

eller•v =eller.v.cos α

Linje ligning i flyet

En linje i det kartesiske planet kan være representert på flere måter, for eksempel:

Det kan tjene deg: Generell parabola -ligning (eksempler og øvelser)

-I påvente av skjema: Ja m Det er skråningen på linjen og b Det er skjæringspunktet mellom linjen med den vertikale aksen, ligningen på linjen er y = mx +b.

-Generell ligning for en rett linje: Øks + av + c = 0, hvor M = a/b Det er skråningen.

I det kartesiske planet er vertikale og horisontale linjer spesielle tilfeller av linjelikningen.

-Vertikale linjer: x = a

-Horisontale linjer: y = k

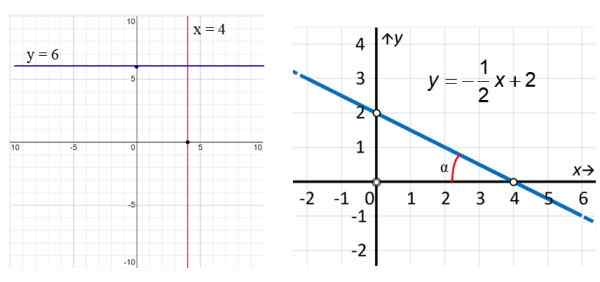Figur 3. Til venstre den vertikale linjen x = 4 og den horisontale linjen y = 6. Til høyre et eksempel på skrå linje. Kilde: f. Zapata.

I eksemplene på figur 3 har den vertikale røde linjen ligning x = 4, mens linjen parallelt med x -aksen (blå) har ligning y = 6. Når det gjelder riktig linje, ser vi at den er skrått og å finne ligningen vi bruker punktene som er fremhevet i figuren: (0,2) og (4.0) på denne måten:

M = (og₂ - og₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

Kuttet på denne linjen med den vertikale aksen er y = 2, Som nevnt fra grafikken. Med denne informasjonen:

y = (-½) x+2

Å bestemme hellingsvinkelen med hensyn til x -aksen er enkel. Jeg føler det:

α = ARCTG (2/4) = 26.6

Derfor er den positive vinkelen fra X -aksen til linjen: 180º - 26.6. = 153.4. plass

Eksempler på skrå linjer

Figur 4. Eksempler på skrå linjer. Kilde: Ian Patterson Wreathful [CC av (https: // CreativeCommons.Org/lisenser/av/2.0)]. Pisas lente tårn. Pixabay.

Skrøkte linjer vises mange steder, det handler om å ta hensyn til å finne dem i arkitektur, sport, ledninger i strømforsyningen, rør og mange flere steder. I naturen er skrå linjer også til stede, som vi vil se nedenfor:

Kan tjene deg: avledningsregler (med eksempler)

Lysstrålene

Solys sprer seg i en rett linje, men jordens avrundede form påvirker måten sollys påvirker overflaten.

På bildet nedenfor kan vi tydelig sette pris på at solstrålene påvirker vinkelrett i de tropiske regionene, men i stedet kommer de skrått til overflaten i de tempererte regionene og i polene.

Derfor kjører solstrålene en lengre avstand gjennom atmosfæren og også varmen sprer seg på en større overflate (se figur). Resultatet er at områder i nærheten av polakkene er kaldere.

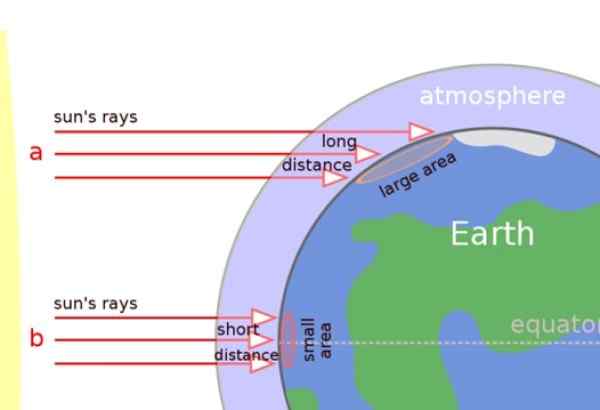Figur 5. Solstrålene påvirker de tempererte sonene og polene, men de er mer eller mindre vinkelrett i tropene. Kilde: Wikimedia Commons.

Linjer som ikke er i samme plan

Når to linjer ikke er i samme fly, kan de fortsatt være skrå eller berømmet, Som de også er kjent. I dette tilfellet er direktørene ikke parallelle, men ikke tilhører samme plan, disse linjene har ingen kryss.

For eksempel er linjer i riktig figur helt klart i forskjellige plan. Hvis de ser ovenfra, blir det observert at de effektivt krysser, men de har ikke et felles punkt. Til høyre ser vi sykkelhjulene, hvis stråler ser ut til å krysse når de ser rett frem.

Figur 6. Skrå linjer som tilhører forskjellige fly. Kilde: Venstre f. Zapata, høyre Pixabay.

Referanser

1. Geometri. Vektordirektør for en linje. Gjenopprettet fra: Juanbragado.er.
2. Larson, r. 2006. Beregning med analytisk geometri. 8. Utgave. McGraw Hill.
3. Matematikk er et spill. Linjer og vinkler. Gjenopprettet fra: Juntadeandalucia.er.
4. Linjer som krysser. Gjenopprettet fra: Teacheraltuna.com.
5. VILLENA, m. Analytisk geometri i R3. Hentet fra: DSPACE.Espol.Edu.Ec.