Andre linjer

Tømmeret til døren til denne hagen er villige på en slik måte at de bestemmer tørre linjer. Kilde: f. Zapata. Pxhere.com

Hva er de tørre linjene?

I flyet, Andre linjer De er de som krysser andre linjer og kurver. Når det gjelder to linjer, er krysset et punkt, mens Secant -linjen ved en kurve kutter dette i to eller flere poeng.

Observer gjerdet til den øvre figuren nøye. På den er trukket flere rette rette farger, betegnet som l₁, L₂ og jeg₃. Pilene i begge sider betyr at linjene er forlenget på ubestemt tid.

Vel, linjene l₁, L₂ og jeg₃ De tørker hverandre, siden hvert par av dem er kuttet på lilla punkter.

I tillegg linjene l₁ og jeg₂, Som l₁ og jeg₃, De bestemmer 4 vinkler med hverandre, to av dem akutte og den andre stump, mens linjene l₂ og jeg₃ De er vinkelrett, noe som betyr at de 4 vinklene som er bestemt av dem er rette.

To parallelle linjer kan aldri være tørre, siden de på grunn av tilstanden deres ikke har noen tilfeldighetspunkter. På sin side er de sammenfallende linjene ikke tørre, ettersom de har mer enn ett poeng til felles.

Kjennetegn på tørkelinjene

• To sekantlinjer har et unikt punkt som kryss.
• Hellingene til to tørkelinjer må være forskjellige. Ja m₁ Det er skråningen på linjen l₁, og M₂ Det er skråningen på linjen l₂, da blir det oppfylt at m₁ ≠ m₂.
• Hellingene til to tørkelinjer vinkelrett på hverandre, hvis respektive bakker er m₁ og M₂, De oppfyller forholdet m₁ = -1/ m₂. I tillegg skal skalarproduktet mellom to vektorer v og eller inneholdt i disse linjene er null, siden definisjonen av skalarprodukt er v eller = v ∙ u ∙ cos θ, være θ vinkelen mellom vektorene.
• En linje kan være sikret på en kurve eller en annen geometrisk figur.
• Når du krysser hverandre, genererer to tørkelinjer 4 vinkler, identiske to til to eller identiske med hverandre.

Kan tjene deg: brøkdeler

Hvordan vite om to linjer er tørre

Fra egenskapene til tørkelinjene beskrevet ovenfor, er det mulig å etablere tre kriterier for å vite om to linjer er tørre:

-Sammenligne bakkene. Hvis disse er forskjellige, er linjene tørre.

-Gjennomføre det skalare produktet mellom to vektorer som er inneholdt i disse linjene, kalt Direktører. Hvis skalarproduktet er ugyldig, er linjene tørre og vinkelrett, og hvis det ikke er null, er det mulig å vite minimumsvinkelen mellom dem, som er den akutte vinkelen som eksisterer mellom linjene.

Forutsatt at denne vinkelen er forskjellig fra 0º, er linjene tørre, og hvis den er lik 0º, er den parallelle linjer.

-Direkte beregning av den akutte vinkelen som finnes mellom linjene, kjent skråningene deres. Dette kan gjøres gjennom formelen som relaterer tangenten til nevnte vinkel med bakkene.

La m₁ og M₂ bakkene, og θ den akutte vinkelen mellom dem. Tangenten til θ er gitt av:

Typer tørkelinjer

Når to linjer tørker hverandre, kan de være følgende typer:

• Skrå, Hvis de er kuttet, danner de to akutte vinkler og to stumpe vinkler. Disse vinklene er supplerende, det vil si summen av målet på vinkelen pluss en av den stumpe vinkelen er lik 180º. Totalt er summen av de 4 vinklene lik 360º.
• Vinkelrett, De som krysser 4 vinkler lik 90º.

Hvordan finne skjæringspunktet mellom to linjer

Hvis to linjer tørker, har de bare ett kuttpunkt, som løser systemet med to lineære ligninger med to ukjente. Hvis linjene er gitt generelt: AX + av = C, sa at systemet med ligninger er:

Kan tjene deg: uendelig sett: egenskaper, eksempler

til₁x + b₁ y = c₁

til₂x + b₂ y = c₂

Hvordan finne skjæringspunktet mellom en linje og en kurve

Når du kjenner ligningene til både linjen og kurven, foreslås ligningssystemet og hvis løsninger tilsvarer skjæringspunktene. Hvis systemet mangler en løsning, er ikke linjen sikret på kurven, og det er heller ikke hvis det er et enkelt skjærepunkt, siden linjen i så fall er tangent til kurven.

For at linjen skal tørke, som det fremgår av begynnelsen, må ligningssystemet ha to eller flere løsninger.

Eksempler på tørkelinjer

Det kartesiske flyet

Det kartesiske planet bestemmes av to linjer, kalt X akse og Axis y, horisontalt og vertikalt, henholdsvis. Disse linjene er vinkelrett og skjæringspunktet deres kalles Opprinnelsen til koordinatsystemet, eller bare opprinnelse.

Diagonalen til en polygon

En polygon er en flat figur på tre eller flere sider, som går sammen med punkter som kalles toppunkter. Et segment som blir sammen med to ikke -samtykke vertikaler er en diagonal av polygonen, og linjen som inneholder nevnte segment er sikret på det aktuelle polygonet.

Et omkretsau

Tauet til en omkrets er segmentet som blir sammen med to av poengene sine. Hovedtauet er diameteren, som nødvendigvis går gjennom sentrum av omkretsen. Vel, linjen som inneholder ethvert tau, inkludert diameteren, er en tørkelinje til omkretsen.

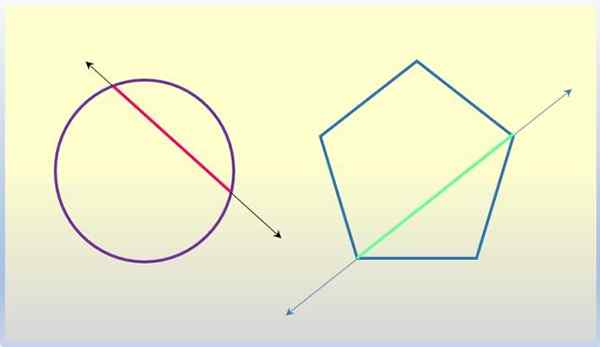Andre linjer til geometriske figurer. Kilde: f. Zapata.

Kryssnøkkelen

Med dette verktøyet er nøttene som holder dekkene til hjulene på kjøretøyene løsne. Armene formlinjer som er tørre og samtidig vinkelrett vinkelrett.

Kan tjene deg: proporsjonal variasjon

Alfabet tekster

Noen alfabetbrev består av rette slag som bestemmer Secant. For eksempel består bokstav X av to slag som er kuttet sammen på ett punkt, og bokstaven T består av to vinkelrett linjer.

Løste øvelser

Oppgave 1

Bestem om linjene gitt av:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Løsning

Hellingen på en linje gitt i formen y = mx + b er verdien av m, det vil si koeffisienten som følger x. Siden m₁ = 5 og m₂ = -2, som er forskjellige, konkluderes med at linjene er tørre.

Oppgave 2

Hva er den akutte vinkelen mellom linjene i trening 1?

Løsning

M -verdiene erstattes direkte₁ = 5 og m₂ = -2 I formelen gitt i de foregående seksjonene:

Derfor er vinkelen mellom linjene θ = arctg 0.777… = 37.9º.

Øvelse 3

Hva er skjæringspunktet mellom linjene i de tidligere øvelsene?

Løsning

Ligningssystemet foreslås som følger:

Hvis løsning er: x = 4/7; y = -1/7 (kan løses ved noen av oppløsningsmetodene for ligningssystemer, eller med en kalkulator).

Derfor er skjæringspunktet mellom linjer: P (4/7; -1/7).

Referanser

1. Analytisk geometri.Info. Andre linjer. Gjenopprettet fra: Geometriaalitics.Info.
2. Larson, r. 2006. Beregning med analytisk geometri. 8. Utgave. McGraw Hill.
3. Linjer som krysser. Gjenopprettet fra: Teacheraltuna.com.
4. Requena, b. Andre linjer. Gjenopprettet fra: Universoformulas.com.
5. VILLENA, m. Analytisk geometri i R3. Hentet fra: DSPACE.Espol.Edu.Ec.