Høyre håndregel

Figur 1. Høyre håndregel. Kilde: Wikimedia Commons. ACDX [CC BY-S (http: // CreativeCommons.Org/lisenser/by-SA/3.0/]].

Hva er den høyre regelen?

De Høyre håndregel Det er en mnemonisk ressurs å etablere retningen og retningen til vektoren som følge av et vektorprodukt eller kryssprodukt. Det er mye brukt i fysikk, siden det er viktige vektorstørrelser som er resultatet av et vektorprodukt. Slik er tilfellet med dreiemoment, magnetisk kraft, vinkelmomentum og magnetisk øyeblikk, for eksempel.

Være to generiske vektorer til og b hvis kryssprodukt er til x b. Modulen til en slik vektor er:

til x b = til.b.sin α

Hvor α er minimumsvinkelen mellom til og b, Mens A og B representerer modulene deres. For å skille vektorer fra modulene deres, brukes dristige bokstaver.

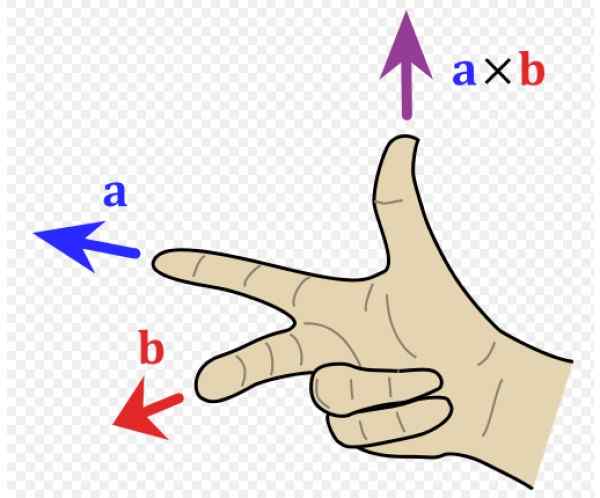
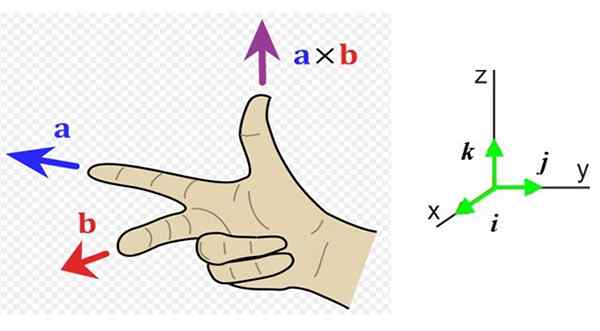
Nå må vi vite retningen og betydningen av denne vektoren, så det er praktisk å ha et referansesystem med de tre retningene i rommet (figur 1 til høyre). Enhetsvektorene Yo, J og k De peker henholdsvis til leseren (ut av siden), til høyre og oppover.

I eksemplet på figur 1 igjen, vektoren til er på vei til venstre (adresse og negativ og pekefingeren til høyre) og vektoren b går til leseren (adresse x positiv, langfingeren til høyre hånd).

Den resulterende vektoren til x b har tommelretning, opp i retning z positivt.

Andre regler for høyre hånd

Denne regelen brukes mye når det er størrelser hvis retning og mening roterer, for eksempel magnetfeltet B produsert av en tynn og rettlinjet ledning som transporterer en strøm.

I dette tilfellet er magnetfeltlinjene konsentriske omkretser med ledningen, og retningen på svingen oppnås med denne regelen på følgende retning av feltet. Vi illustrerer konseptet i figur 2.

Kan tjene deg: Elastiske sjokk: I en dimensjon, spesielle tilfeller, øvelser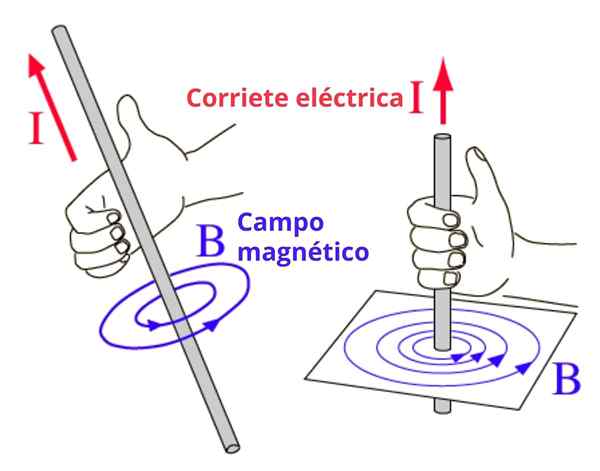Figur 2. Høyre håndregel for å bestemme betydningen av magnetfeltsirkulasjonen

Alternativ regel om høyre hånd

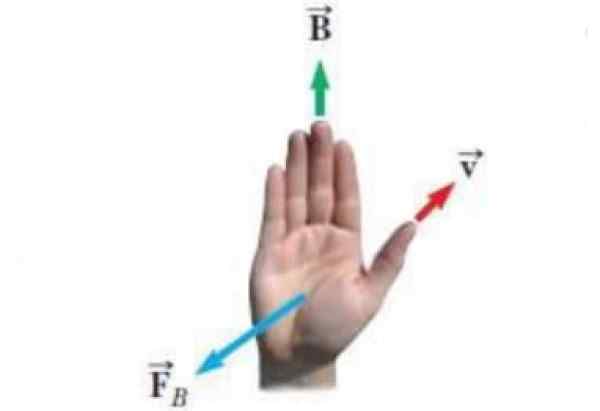
Følgende figur viser en alternativ form for høyre håndregel. Vektorene som vises i opplysningen er:

• Hastighet v av en punktlig belastning som.
• Magnetfeltet B som belastningen beveger seg i.
• F_B Kraften som magnetfeltet utøver på lasten.

Figur 3. Alternativ regel om høyre hånd. Kilde: Wikimedia Commons. Experticuis [CC BY-SA (https: // CreativeCommons.Org/lisenser/by-SA/4.0)]

Ligningen for magnetisk kraft er F_B = qv x B og regelen om høyre hånd for å kjenne retningen og følelsen av F_B Det gjelder slik: tommelpunktene i henhold til V er de resterende fire fingrene plassert i henhold til felt B. Så F_B Det er en vektor som kommer ut av håndflaten, vinkelrett på den, som om den skyver belastningen.

Noter det F_B ville peke i motsatt retning hvis belastningen som var negativ, siden vektorproduktet ikke er kommutativ. Faktisk:

til x B = - B x til

applikasjoner

Høyre regelen kan brukes på forskjellige fysiske størrelser, la oss vite noen av dem:

Vinkelhastighet og akselerasjon

Begge vinkelhastighetene Ω Som vinkelakselerasjon α De er vektorer. Hvis et objekt roterer rundt en fast akse, er det mulig vinkelhastighet Ω.

For sin del vinkelakselerasjonen α vil ha samme adresse som Ω, Men betydningen avhenger av om Ω øker eller reduserer størrelsen over tid. I det første tilfellet har begge samme retning og mening, men i det andre vil de ha motsatte sanser.

Kan tjene deg: Watt lov: Hva er, eksempler, applikasjoner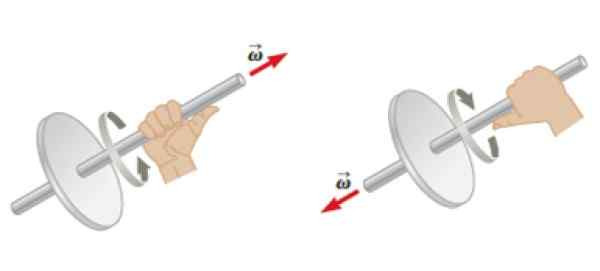Figur 4. Høyre regel brukt på et objekt i rotasjon for å bestemme retningen og retningen på vinkelhastigheten. Kilde: Serway, R. Fysisk.

Vinkelmomentet

Vinkelvektoren L_ENTEN av en partikkel som roterer rundt en viss akse eller er definert som vektorproduktet til sin øyeblikkelige posisjonsvektor r  og mengden lineær bevegelse p:

L = r x p

Høyre -hånd -regelen brukes på denne måten: pekefingeren er plassert i samme retning og retning av r, Langfingeren i p, begge på et horisontalt plan, som i figuren. Automatisk strekker tommelen seg vertikalt oppover på å peke ut retningen og retningen på vinkelmomentum L_ENTEN.

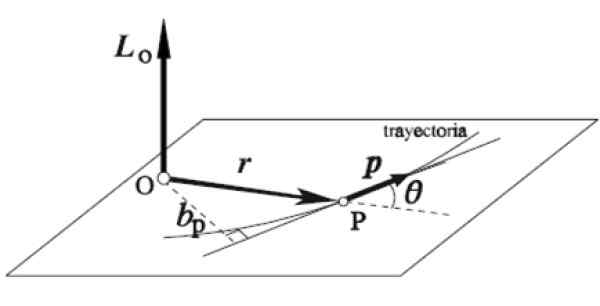Figur 5. Vinkelvektoren. Kilde: Wikimedia Commons.

Øvelser

Oppgave 1

Spinnet på figur 6 går raskt med vinkelhastighet Ω og dens symmetriaksen ble brutt saktere rundt den vertikale aksen z. Denne bevegelsen kalles presesjon. Beskriv kreftene som virker på spinnet og effekten de gir.

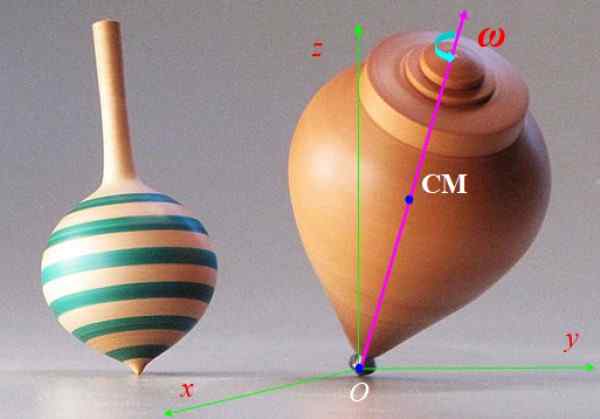Figur 6. Spinning spinn. Kilde: Wikimedia Commons.

Løsning

Kreftene som virker på spinnet er normale N, brukt på støttepunktet med bakken eller mer vekten mg, påført i sentrum av mass CM, med g Alvorlighetsgradsakselerasjonsvektoren, rettet vertikalt ned (se figur 7).

Begge kreftene er balanserte, derfor beveger spinnet seg ikke. Imidlertid gir vekten et dreiemoment eller dreiemoment τ Netto om poenget eller gitt av:

τ_ENTEN = r_ENTEN x F, med F = Mg.

Som r og Mg De er alltid på flyet når spinnet svinger, i henhold til regelen om høyre hånd dreiemomentet τ_ENTEN Det ligger alltid i flyet Xy, vinkelrett begge a r som g.

Noter det N produserer ikke et dreiemoment med hensyn til O, fordi dens vektor r Angående eller er null. Det dreiemomentet gir en endring i vinkelmomentet som forårsaker presesjonen til spinnet rundt Z -aksen.

Kan tjene deg: Termodynamisk balanse: Klasser og applikasjoner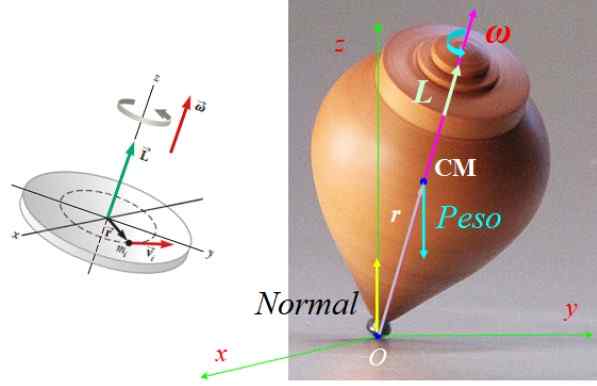Figur 7. Krefter som virker på spinnet og dens vinkelmomentvektor. Kilde til venstre figur: Serway, r. Fysikk for vitenskap og ingeniørfag.

Oppgave 2

Påpeke retningen og retningen til vinkelmomentvektoren L av trumpen av figur 6.

Løsning

Ethvert punkt med spinnet har masse m_Yo, hastighet v_Yo og posisjonsvektor r_Yo, Når det dreier seg om Z -aksen. Vinkelmomentet L_Yo av nevnte partikkel er:

L_Yo = r_Yo x p_Yo = r_Yo x m_Yov_Yo

Gitt r_Yo og v_Yo De er vinkelrett, størrelsen på L er:

L_Yo = m_Yor_Yov_Yo

Den lineære hastigheten v er relatert til vinkelhastighet Ω gjennom:

v_Yo = r_YoΩ

Derfor:

L_Yo = m_Yor_Yo (r_YoΩ) = m_Yor_Yo²Ω

Den totale vinkelmomentet til tromposen er summen av vinkelmomentet til hver partikkel:

L = (∑M_Yor_Yo² ) Ω

∑ m_Yor_Yo²  Det er treghetsmomentet i spinnet, da:

L= JegΩ

Derfor L og Ω De har samme retning og mening, som vist i figur 7.