Fibonacci -serieegenskaper, naturlige forhold, applikasjoner

De O -serien Fibonacci -suksess er en sekvens av tall som oppnås ved å begynne med 0 og 1, fortsetter med summen av dem: 0 + 1 = 1, deretter summen av de foregående to: 1 + 1 = 2 og så videre.

Etter denne prosedyren er de andre begrepene oppnådd, la oss se: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13 ..

Første tall i Fibonacci -serien

Prosedyren gjentas så mange ganger du vil. På denne måten skaffer Fibonaccis suksess skjemaet: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Tallene som gjør det kalles Fibonacci -tall.

[TOC]

Historie

Fibonaccis suksess kalles en italiensk matematiker som bodde i middelalderen: Leonardo de Pisa, også kjent som Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo tilbrakte barndommen i Nord -Afrika og reiste gjennom Middelhavet, hvor han kjente det indo -arabiske nummereringssystemet og var gledelig med ham. Sannsynligvis lærte Leonardos arabiske lærere ham om suksessen, som allerede var kjent av hinduistiske matematikere.

Deretter, da han kom tilbake til Pisa Fibonacci, skrev en bok som heter Liber Abaci (Abacus bok), der i tillegg til å fremheve fordelene med indo -arabiske tall i møte med romersk nummerering og introdusere 0, reiste han et problem om reproduksjon av kaniner.

Og løsningen på dette problemet er nettopp antallet Fibonacci -suksessen.

Leonardo de Pisa ble ikke tildelt opprettelsen av arven; Han nevnte det bare i sin bok som en nysgjerrighet, som vakte oppmerksomheten til mange lærde som fulgte ham. Blant disse var den nittende -århundre franske matematikeren Edouard Lucas, som da hun studerte suksessen døpte henne med navnet på middelalderens vismann som gjorde det kjent i Vesten.

Problemet med Fibonacci -kaniner

Problemet sier: Det er et par kaniner som lever for alltid, som om to måneder er fruktbart. Når modenheten er oppnådd, har de et par babyer med forskjellig sex hver måned, noe som også tar to måneder å reprodusere og ha et månedlig par kaniner.

Kan tjene deg: De Morgan Laws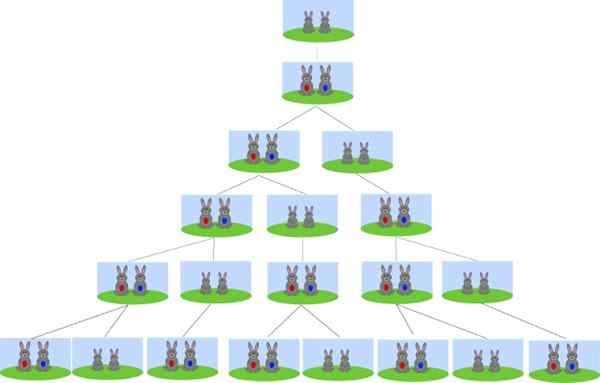Opprinnelsen til Fibonaccis suksess er i problemet med reproduksjon av kaniner. Kilde: Wikimedia Commons.

Fra og med et par nyfødte kaniner, hvor mange par kaniner vil være om en måned? Hvor mange par kaniner vil være etter 2, 3 og 4 måneder? Og hvor mange som vil være etter 6 måneder?

Svaret er i fibonacci -tall. Etter 1 måned er det 1 par kaniner, det opprinnelige paret, da de bare reproduserer etter 2 måneder.

Etter 2 måneder er det 2 par kaniner: det opprinnelige paret og deres første kull.

Etter 3 måneder vil vi ha 3 par, inkludert det opprinnelige paret, deres første kull og en ny.

Når vi når den fjerde måneden, vil vi ha det opprinnelige paret, det første kullet som igjen har sine første barn, kullet i den tredje måneden og et nytt kull. Totalt 5 par kaniner.

Men dette er antallet av Fibonacci -sekvensen, derfor vil det etter 6 måneder være 13 par kaniner, siden parene i de to foregående månedene hver måned blir lagt til.

Fibonacci -serieegenskaper

Her er noen interessante egenskaper ved Fibonacci -suksessen.

Eiendom 1

Den rekursive formelen for å finne vilkårene for suksessen er:

til_N+1 = a_n + til_N-1  For n større enn eller lik 2.

Hvor n = 2, 3, 4, ... det vil si å finne syvende periode A₇, Vi gjør n = 6, slik at 6+1 = 7. Vi må vite vilkårene til₅  allerede₆, av listen som vises i introduksjonen til₅ = 5 og a₆ = 8, derfor til₇ = 5+8 = 13.

Eiendom 2

Hvis de to begrepene vi ønsker å finne ikke er kjent, kan vi bruke følgende formel:

Det kan tjene deg: Tesseldos: Karakteristikk, typer (vanlig, uregelmessig), eksempler

Eiendom 3

Tallene a_n allerede_N+1 er  Coprimos, det vil si at de er søskenbarn med hverandre, noe som betyr at de ikke har noen felles faktorer til felles.

Eiendom 4

En veldig interessant eiendom er den av kvotienten mellom vilkårene til_2n allerede_n, som er verdt 1, når n = 1. Det er å si:

til₂ / til₁ = 1

Vi kan enkelt sjekke det med listen over fibonacci -tall.

På den annen side, hvis n ≠ 1, er kvotienten:

til_2n / til_n = a_n  + 2_N-1

For eksempel hvis n = 3, så a _2n = a₆ = 8 og₃ = 2. Da så:

8/2 = 2 + 2. til₂ = 2 + 2. 1

Faktisk: 8/2 = 4 og 2 + (2.1) = 4. Det kan bekreftes at enhver n -verdi er oppfylt.

Eiendom 5

Forholdet r_n = a_N+1 / til_{n ,} Når n blir stor, konvergerer du Gull grunn enten Aurea proporsjon, Et irrasjonelt tall som ofte oppstår i naturen, gitt av:

Naturlige forhold til Fibonacci -suksessen

Fibonaccis suksess i planter

Manifestasjonene av Fibonacci -suksessen florerer i plantekongeriket

Grenene av visse trær kommer ut hvert år i henhold til Fibonacci -suksessen. Det første året vokser bagasjerommet uten å kaste noen grener, etter ett år produserer den en og så i løpet av hvert år. På sin side kan hver gren kaste en annen ny etter ett år, akkurat som kaninene reproduserer.

Solsikkeblomstersenteret inneholder frøene anordnet i logaritmiske spiralstråler, i begge forstand, hvis mengder tilsvarer to påfølgende fibonacci -tall.

Fibonacci -tall er til stede i antall solsikke- og margarittblomster kronblader, så vel som i mange mønstre der planter har bladene sine.

Kan tjene deg: ordinær variabel

Eksperter sier at på denne måten optimaliserer planter plassen for blader og blomster for å ha optimal vekst.

Med et sentralt punkt som utgangspunkt, vokser disse strukturene og får sollys, derfor må de nye bladene og kronbladene dekke så lite som mulig de som kom ut først. Og den beste måten å oppnå dette på er å ta i bruk et vekstmønster når det gjelder Fibonacci -sekvensen.

Fibonaccis suksess hos dyr

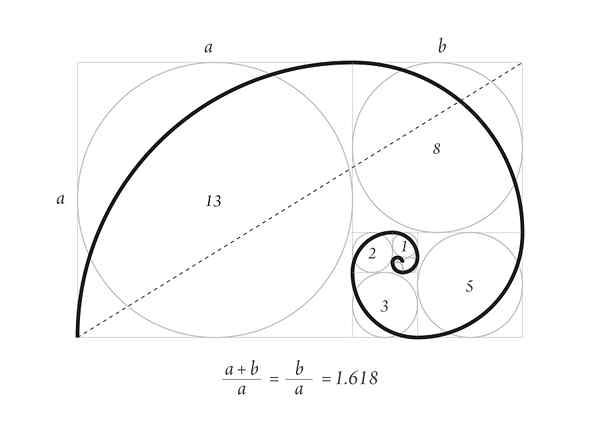Dureros spiral med de første antall Fibonaccis suksess

Den holdbare spiralen til det overlegne bildet er en del av vekstmønsteret til skjellene i marine dyr og hornene til noen drøvtyggere.

Begynn med to firkanter 1, den ene på toppen av den andre, deretter en kvadrat med side 2 ved siden av, som utgjør et rektangel på side 3, hvis sider har den gyldne proporsjonen.

Nedenfor er en kvadrat med side 3 og til venstre en kvadrat med side 5. Over er det en kvadrat med side 8 og til høyre en kvadrat med side 13. Dette er de første tallene i suksessen.

Endelig trekkes spiralen ved å berøre punktene i hjørnene på rutene, som sett på figuren.

applikasjoner

Fibonaccis suksess brukes på forskjellige felt:

-I kunsten vises den gyldne andelen relatert til rekkefølgen av Fibonacci hos mennesker og ting representert av store artister som Leonardo da Vinci, Miguel Ángel og Alberto Durero.

-Andelene av partneren i Athen reagerer også på gullnummeret.

-I komposisjonene til Mozart, Beethoven, Schubert og Debussy.

-Å designe objekter hvis proporsjoner ser harmoniske ut for menneskelige øyne, for eksempel kredittkort, containere, flagg.

-I aksjemarkedet brukes det til å forutsi hvilke priser som går tilbake.

Referanser

1. Fibonacci -suksess. Gjenopprettet fra: Blogeducastur.er.
2. Stewart, J. 2007. Forkalkning. 5. plass. Utgave. Cengage Learning.
3. Vargas, m. Fibonacci -suksessapplikasjoner. Gjenopprettet fra: Matesup.Cl.
4. Wikipedia. Fibonacci -nummer. Hentet fra: i.Wikipedia.org.