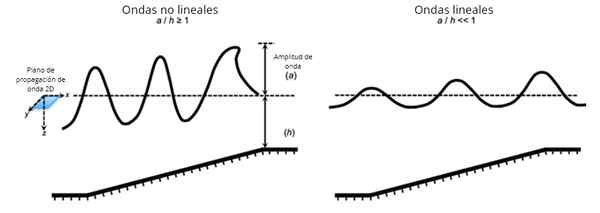
Lineære bølger konsept, egenskaper, eksempler

De Lineære bølger Dette er de der superposisjonsprinsippet er aktuelt, det vil si de der bølgeformen og dens rom-tidsutvikling kan oppnås som summen av grunnleggende løsninger, for eksempel harmonisk type. Ikke alle bølger oppfyller superposisjonsprinsippet, som ikke er i samsvar med det kalles ikke-lineale bølger.

Den "lineære" valør.

Bølgene som sees i det fjerne er lineære bølger, men de skremte bølgene i forgrunnen er ikke-linjer. Kilde: Pixabay.

På den annen side tilfredsstiller ikke-lineale bølger bølge ligninger som har kvadratiske eller høyere grader i den avhengige variabelen eller i deres derivater.

Noen ganger er det forvirret til lineære bølger med langsgående bølger, som er de der vibrasjon skjer i samme utbredelsesretning, for eksempel lydbølger.

Men langsgående bølger, så vel som tverrgående, kan igjen være lineære eller ikke-lineære, avhengig av, blant andre faktorer, amplituden til den første forstyrrelsen og miljøet de sprer seg.

Det forekommer generelt at når den innledende forstyrrelsen er av liten amplitude, er ligningen som beskriver utbredelsen av bølgen, av lineær type eller kan stilles ved visse tilnærminger, selv om den ikke alltid er slik.

[TOC]

Differensialligning i lineære bølger

I et lineært medium kan en begrenset bølgeform i rom og tid representeres ved summen av sinus eller kosinusbølgefunksjoner av forskjellige frekvenser og bølgelengder via Fourier -serien. 

Lineære bølger har alltid en differensialligning av den lineære typen tilknyttet, hvis løsning representerer prediksjonen om hva som vil være forstyrrelsen i bakre øyeblikk av en innledende forstyrrelse lokalisert romlig i det første innledende øyeblikk.

Den klassiske lineære bølge -ligningen, i en enkelt romlig dimensjon, hvis løsninger er lineære bølger er:

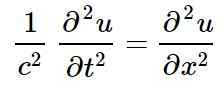
I forrige ligning eller representerer forstyrrelsen av en viss fysisk mengde i stillingen x Og for øyeblikket t, det er å si eller Det er en funksjon av x og t:

Det kan tjene deg: Hva er Coplanares -vektorer? (Med løste øvelser)

u = u (x, t)

For eksempel, hvis det er en lydbølge i luften, eller Det kan representere variasjonen av trykket med hensyn til dens verdi uten å forstyrre.

I tilfelle av en elektromagnetisk bølge, eller representerer det elektriske feltet eller magnetfeltet som svinger vinkelrett på forplantningsretningen.

I tilfelle av et spent tau, eller representerer kryssforskyvningen med hensyn til balansen i tau -likevekten, som vist i følgende figur:

Bølgeform i et gitt øyeblikk, i tilfelle av lineære bølger, er denne formen overlappingen av sinusformede bølger med forskjellig frekvens og bølgelengder. Kilde: f. Zapata.

Differensialligningsløsninger

Hvis du har to eller flere løsninger av den lineære differensialligningen, vil hver løsning multiplisert med en konstant være en løsning og vil også være summen av dem. 

I motsetning til ikke-lineære ligninger, innrømmer waveline-ligninger harmoniske løsninger av typen: 

eller₁= A⋅sen (k⋅x - ω⋅t) og eller₂= A⋅sen (k⋅x + ω⋅t) 

Dette kan verifiseres ved enkel substitusjon i den lineære bølge -ligningen.

Den første løsningen representerer en progressiv bølge som går videre til høyre, mens den andre til venstre raskt C = ω/k.

Harmoniske løsninger er karakteristiske for lineære bølgefeller.

På den annen side er den lineære kombinasjonen av to harmoniske løsninger også en løsning på den lineære bølge -ligningen, for eksempel:

u = a₁ cos (k₁⋅x - ω₁⋅t) + a₂ Synd (k₂⋅x - ω₂⋅t) er løsning.

Det mest relevante kjennetegn ved lineære bølger er at enhver form for bølge, uansett kompleks, kan oppnås ved en sum av enkle harmoniske bølger i bryst og kosinus:

u (x, t) = a₀ + ∑_n TIL_n cos (k_n⋅x - ω_n⋅t) + ∑_m B_m Synd (k_m⋅x - ω_m⋅T).

Dispersive and Non -Dispersive Linear Waves

I den klassiske lineære bølge ligningen, c representerer hastigheten på forplantning av pulsen.

Ikke -dispersive bølger

I tilfeller hvor c Det er en konstant verdi, for eksempel de elektromagnetiske bølgene i tomrommet, deretter en puls i det første øyeblikket t = 0 Form f (x) Det sprer seg i henhold til:

u (x, t) = f (x - c⋅t)

Uten å lide noen forvrengning. Når dette skjer, sies det at mediet er ikke-designet.

Spredende bølger

Imidlertid, i spredende medier, kan forplantning C -hastigheten avhenge av bølgelengden λ, det vil si: c = c (λ).

Kan tjene deg: kontinuitetsligning

Elektromagnetiske bølger er spredende når du reiser gjennom et materielt medium. Også overflatebølgene i vannet beveger seg med forskjellig hastighet i henhold til vannets dybde.

Hastigheten som en harmonisk bølge forplanter seg A⋅sen (K⋅x - ω⋅t) er Ω/k = c og fasehastigheten kalles. Hvis mediet er spredende, så c Det er en bølgeallfunksjon k: C = c (k), hvor k Det er relatert til bølgelengden ved hjelp av K = 2π/λ.

Spredningsforhold

Forholdet mellom frekvens og bølgelengde kalles spredningsforhold, som uttrykt i form av vinkelfrekvens Ω Og bølgenummeret k er: Ω = c (k) ⋅k.

Noen spredningsforhold Karakteristikker av lineære bølger er følgende:

I bølgene der bølgelengden (avstanden mellom rygger) er mye større enn dybden H, Men at bredden er mye mindre enn dybden spredningsforholdet er:

Ω = √ (GH) ⋅K

Derfra konkluderes det med at de spredte seg med konstant hastighet √ (GH) (Ikke -splittig halvparten).

Men bølgene i veldig dypt vann er spredende, siden spredningsforholdet deres er:

ω = √ (g/k) ⋅k

Dette betyr at fasehastigheten Ω/k Det er variabelt og avhenger av bølgelengden og derfor bølgelengden til bølgen.

Gruppehastighet

Hvis to harmoniske lineære bølger overlapper hverandre, men avanserer i forskjellige hastigheter, samsvarer ikke gruppehastigheten (det vil si av bølgepakken).

Gruppehastighet v_g Det er definert som frekvensderivatet med hensyn til bølgetallet i spredningsforholdet: v_g = Ω '(k).

Følgende figur viser overlappingen eller summen av to harmoniske bølger eller₁= A⋅sen (k₁⋅x - ω₁⋅T) og eller₂= A⋅sen (k₂⋅x - ω₂⋅T) som reiser i forskjellige hastigheter v₁= Ω₁/k₁ og v₂= Ω₂/k₂. Legg merke til hvordan gruppehastighet er forskjellig fra fasehastigheten, i dette tilfellet er gruppehastigheten ∆ω/∆K.

Det kan tjene deg: magnetiske egenskaper til materialer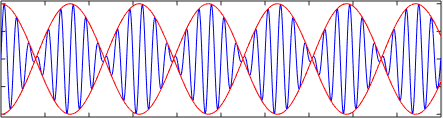Lineær (blå) bølge i et spredende medium. Den røde kurven er lagt til for å fremheve at gruppehastigheten er forskjellig fra forplantningshastigheten

Avhengig av spredningsforholdet kan fasehastigheten og gruppehastigheten, i motsatte retninger, til og med ha motsatte retninger.

Eksempler på lineære bølger

Elektromagnetiske bølger

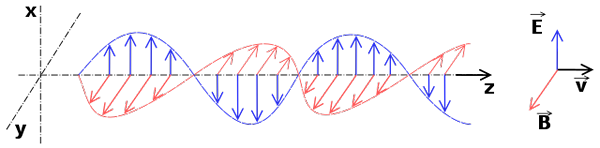Elektromagnetiske bølger som utgjør elektromagnetisk stråling

Elektromagnetiske bølger er lineære bølger. Dens bølge ligning trekkes fra ligningene av elektromagnetisme (Maxwell -ligninger) som også er lineære.

Schrödingers ligning

Det er ligningen som beskriver dynamikken til partiklene i atomskalaen, der de bølgende egenskapene er relevante, for eksempel tilfellet med elektroner i atomet.

Da er "elektronbølgen" eller bølgefunksjonen som den også kalles en lineær bølge.

Bølger i dypt vann

Lineære bølger er også de der amplituden er mye lavere enn bølgelengden og bølgelengden mye større enn dybden. Bølgene i dypt vann følger den lineære teorien (kjent som Airys bølgende teori).

Imidlertid er bølgen som nærmer seg kysten og danner den karakteristiske kammen som rulles (og som surfere elsker) en ikke -lineær bølge.

Lyd

Ettersom lyd er en liten forstyrrelse av atmosfæretrykk, regnes det som en lineær bølge. Imidlertid er sjokkbølgen av en eksplosjon eller bølgefront av et supersonisk plan, typiske ikke -lineære bølgeeksempler.

Bølger på et anspent tau

Bølgene som sprer seg gjennom et anspent tau er lineære, forutsatt at den første pulsasjonen er liten, det vil si at den elastiske grensen for tauet ikke overskrides.

Lineære bølger på strengene gjenspeiles i endene og overlappingen, noe.

Referanser

1. Griffiths G og Schiesser w. Lineære og ikke -lineære bølger. Gjenopprettet fra: Sholarpedia.org.
2. Whitham G.B. (1999) "Lineære og ikke -lineære bølger". Wiley. 
3. Wikipedia. Ikke -lineære bølger. Gjenopprettet fra: er.Wikipedia.com
4. Wikipedia. Ikke -lineær akustisk. Hentet fra: i.Wikipedia.com
5. Wikipedia. Bølger. Hentet fra: i.Wikipedia.com
6. Wikiwaves. Ikke -lineære bølger. Gjenopprettet fra: wikiwaves.org