Aksiale symmetriegenskaper, eksempler og øvelser

De Aksial symmetri Det oppstår når punktene til en figur sammenfaller med punktene til en annen figur ved hjelp av en rett mediatrix som kalles symmetri -aksen. Det kalles også radiell, rotasjon eller sylindrisk symmetri.

Det brukes vanligvis i geometriske figurer, men det er lett observerbar i naturen, siden det er dyr som sommerfugler, skorpioner, hyller eller riktig mennesker som presenterer aksial symmetri.

På dette bildet av horisonten til byen Toronto og dens refleksjon i vannets aksiale symmetri er utstilt. (Kilde: Pixabay)

[TOC]

Hvordan finne den symmetriske aksiale

For å finne den symmetriske aksiale P 'til et P -punkt med hensyn til en linje (L) utføres følgende geometriske operasjoner:

1.- Vinkelrett på linjen (L) spores som passerer gjennom punkt P.

2.- Avlyttingen av de to linjene bestemmer et punkt eller.

3.- Lengden på PO -segmentet måles, deretter kopieres denne lengden på linjen (PO) som starter fra eller i retning av p a eller bestemmer punktet P '.

4.- Punkt p.

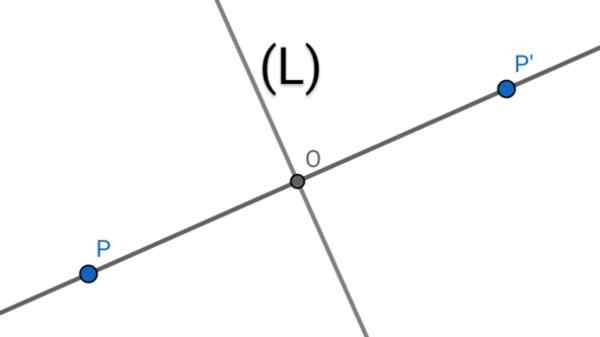Figur 1. To punkter P og P 'er aksialt symmetrisk for en akse (L) hvis nevnte akse er mediatrix av PP -segmentet'

Egenskaper for aksial symmetri

- Axial symmetri er isometrisk, det vil si avstandene til en geometrisk figur og dens tilsvarende symmetriske.

- Målet på en vinkel og den for den symmetriske er det samme.

- Det symmetriske aksialet til et punkt på symmetriaksen er selve punktet.

Det kan tjene deg: Gauss-Seidel Method: Forklaring, applikasjoner, eksempler

- Den symmetriske linjen til en linje parallell med symmetriaksen er også en bås parallell med nevnte akse.

- En sikringslinje til symmetriaksen er symmetrisk.

- Det symmetriske bildet av en linje er en annen linje som danner en vinkel med symmetriaksen med samme mål som den opprinnelige linjen.

- Det symmetriske bildet av en linje vinkelrett på symmetriaksen er en annen linje som overlapper den første.

- En linje og dens aksiale symmetriske linje danner en vinkel hvis bisektor er symmetriaksen.

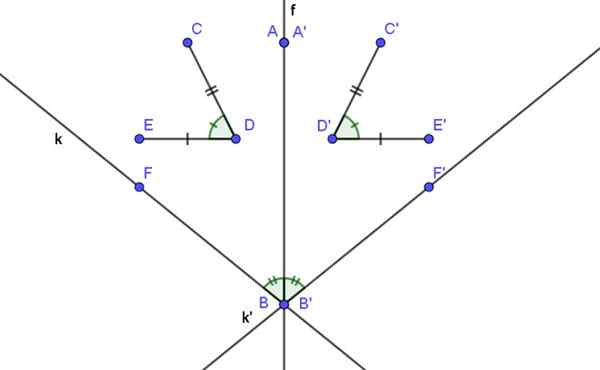Figur 2. Axial symmetri bevarer avstander og vinkler.

Eksempler på aksial symmetri

Naturen viser rikelig med eksempler på aksial symmetri. For eksempel kan du se symmetrien til ansiktene, av insekter som sommerfugler, refleksjonen rundt overflater av rolige vann og speil eller bladene på plantene, blant mange andre.

Figur 3. Denne sommerfuglen viser nesten perfekt aksial symmetri. (Kilde: Pixabay) Figur 4. Ansiktet til denne jenta har aksial symmetri. (Kilde: Pixabay)

Aksiale symmetriøvelser

Oppgave 1

Du har trekanten av hjørner A, B og C hvis kartesiske koordinater er henholdsvis A = (2, 5), B = (1, 1) og C = (3.3). Finn de kartesiske koordinatene til den symmetriske trekanten med hensyn til Y -aksen (ordinatene) Axis).

Løsning: Hvis et punkt P har koordinater (x, y), er det symmetrisk med hensyn til ordinatene (y-aksen). Med andre ord.

Kan tjene deg: uendelig sett: egenskaper, eksempler

I dette tilfellet vil den symmetriske trekanten av hjørner A ', B' og C 'ha koordinater:

A '= (-2, 5); B '= (-1, 1) og c' = (-3, 3) som kan kontrolleres i figur 6.

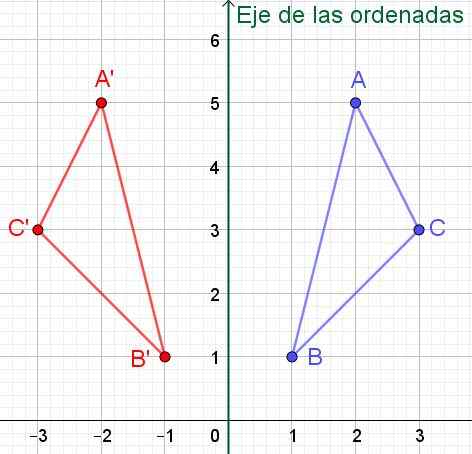Figur 6. Hvis et punkt har koordinater (x, y), vil dets symmetriske med hensyn til y-aksen (ordinatene) ha koordinater (-x, y).

Oppgave 2

I referanse til ABC -trekanten og dens symmetriske a'b'c 'av øvelse 1, må du sjekke at de tilsvarende sidene av den opprinnelige trekanten og dens symmetriske har samme lengde.

Løsning: For å finne avstanden eller lengden på sidene bruker vi den euklidianske avstandsformelen:

d (a, b) = √ ((bx-ax)^2 + (by-ay)^2) = √ ((1-2)^2 + (1-5)^2) = √ ((-1 )^2 + (-4)^2) = √ (17) = 4.123

Deretter beregnes lengden på den symmetriske siden som tilsvarer'B ':

D (a ', b') = √ ((bx'-ax ')^2 +(by'-y^2) = √ ((-1 +2)^2 +(1-5)^2) = √ ((1)^2 + (-4)^2) = √ (17) = 4,123

På denne måten er det bevist at aksial symmetri bevarer avstanden mellom to punkter. Prosedyren kan gjentas for de to andre sidene av trekanten og dens symmetriske for å sjekke invariansen i lengden. For eksempel | Ac | = | A'c '| = √5 = 2.236.

Øvelse 3

I forhold til ABC -trekanten og dens symmetriske a'b'c 'av øvelse 1, må du sjekke at de tilsvarende vinklene til den opprinnelige trekanten og deres symmetriske har samme vinkelmål.

Løsning: For å bestemme målene for vinklene Bac og B'a'c 'vil skalarproduktet til vektorene bli beregnet først AB med Ac Og så skalarproduktet av A'b ' med A'c '.

Husker det:

A = (2, 5), b = (1, 1) og c = (3.3)

A '= (-2, 5); B '= (-1, 1) og c' = (-3, 3).

Du har:

AB = y Ac =

på samme måte

A'b ' = y Ac =

Kan tjene deg: Lamy teorem

Da blir følgende skalarprodukter funnet:

Ab⋅ac = ⋅ = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7

på samme måte

A'b'⋅a'c ' = ⋅ = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7

Målet på BAC -vinkelen er:

∡Bac = Arccos ( Ab⋅ac / (|Ab |⋅ |AC |)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Tilsvarende er målet på vinkelen b'a'c ':

∡b'a'c '= Arccos ( A'b'⋅a'c ' / (|A'b '|⋅ |A'c '|)) = 

Arccos (7 / (4,123⋅2,236)) = 40,6º

Konklusjoner at aksial symmetri bevarer målet på vinkler.

Oppgave 4

Være et punkt p koordinat (a, b). Finn koordinatene til dets symmetriske aksiale p 'med hensyn til linjen y = x.

Løsning: Vi vil kalle (a ', b') til koordinatene til det symmetriske punktet p 'med hensyn til linjen y = x. Midtpunktet m av segmentet pp 'har koordinater ((a+a')/2, (b+b ')/2) og er også på linjen y = x, så følgende likhet er oppfylt:

A + a '= b + b'

På den annen side har segmentet PP 'i påvente av -1 for å være vinkelrett på linjen y = x av skråningen 1, så følgende likhet er oppfylt:

B - b '= a' -a

Å rydde de to likestillingene før 'og B' er det konkludert med at:

a '= b og hva b' = a.

Det vil si gitt et punkt P (a, b), dets symmetriske aksiale med hensyn til linjen y = x er p '(b, a).

Referanser

1. Arce m., Blázquez og andre. Flystransformasjoner. Gjenopprettet fra: EducutMxli.Filer.WordPress.com
2. CC -beregning. Aksial symmetri. Gjenopprettet fra: Beregning.DC
3. Superprof. Aksial symmetri. Gjenopprettet fra: Superprof.er
4. Wikipedia. Aksial symmetri. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Symmetri sirkulær. Hentet fra: i.Wikipedia.com