Sammensatt suksess

Suksess sammensatt av gule og blå firkanter. Kilde: f. Zapata

Hva er en sammensatt suksess?

EN sammensatt suksess Den består av en sekvens av elementer, laget av to (eller flere) forskjellige og alternative suksesser. Hver av disse suksessene har en bestemt regel, som brukes til å finne sine respektive elementer.

Elementene trenger ikke å være numeriske, og kunne være figurer, symboler eller bokstaver, men de som er basert på tall kalles aritmetiske suksesser. Figuren som artikkelen vår begynner viser en sammensatt suksess fra gule og blå firkanter.

I denne rekkefølgen starter den fra et stort firkant bestående av 8 gule firkanter og en blå firkant. For å få følgende begrep blir en gul firkant lagt til venstre eller høyre for den første og tredje raden med firkanter. Plassen som resulterer i den sentrale raden er fylt med en blå firkant.

Hver figur i sekvensen kalles begrep. Hvis du vil finne den femte termin, må du legge til en gul firkant til høyre for den første og tredje rekken, og en blå firkant i andre rad:

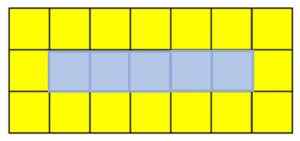Femte termin av en rekke gule og blå firkanter. Kilde: f. Zapata

Forklaring

I sammensatte suksesser oppnås vilkårene ved å veksle vilkårene i to eller flere uavhengige enkle suksesser. For bedre å forstå ideen, bør den gjennomgås detaljene i en enkel suksess.

For eksempel består følgende enkle rekkefølge av de naturlige tallene:

2, 4, 6, 8, 10, 12 ..

Suspensive punkter indikerer at rekkefølgen har uendelige vilkår.

Hvert av vilkårene er betegnet med et lite bokstav og et nummer, som et abonnement. Dette tallet indikerer posisjonen eller indeks av hvert begrep. I forrige rekkefølge kan du skrive:

til₁ = 2; til₂ = 4; til₃ = 6; til₄ = 8 ..

Det er veldig praktisk å ha en måte å beregne ethvert begrep som er ønsket for rekkefølgen, det vil si dens spesielle regel. Med henne N-ésimo-termin, enten Generelt begrep, betegnet som en_n.

Kan tjene deg: Egenskaper for likhet

Fortsetter med eksemplet på suksessen med jevnt tall, kan du etablere måten å beregne begrepet n-ésimo, fra forrige periode:

til_n = a_N-1 + 2

Hvor du skal_N-1 Det er begrepet som går foran_n.

Selvfølgelig ville det være bedre å vite det generelle begrepet uten å avhenge av andre vilkår. I denne rekkefølgen er det lett å merke seg at ethvert begrep multipliserer med 2 posisjonen det inntar, gitt abonnementet på begrepet begrepet. På denne måten er det skrevet:

til_n = 2n

De gamle grekerne kjente allerede suksessene til jevn og rare tall. Etterfølgelsen av rare naturlige tall kan i mellomtiden skrives som:

1, 3, 5, 7, 9, 11 ..

Og å kombinere arven etter de jevnt tallene med det rare, følgende sammensatte suksess er:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Hvis resultat er settet med naturlige tall.

Vilkår for en sammensatt suksess

Det kan være morsomt å prøve å finne forholdet som finnes i en sekvens av tall, som det må observeres nøye og prøve å identifisere om det er en sammensatt suksess.

Den generelle formen for en rekkefølge sammensatt av to suksesser vil være:

til₁, b₁, til₂, b₂, til₃, b₃, til₄, b₄,..

Hvor du skal₁, til₂, til₃, til₄,... er vilkårene i den første suksessen og b₁, b₂, b₃, b₄,... de av det andre. De er alltid ispedd, som tilfellet er i dette eksemplet:

7, 8, 14, 16, tjueen, 24, 28, 32, 35..

Hva vil være begrepet som følger?

For å vite, kjenn suksessen i to alternative sett med tall, som følger:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

I den første av disse settene vises multiplene på 7:

til₁ = 7 × 1 = 7; til₂ = 7 × 2 = 14; til₃ = 7 × 3 = 21; til₄ = 7 × 4 = 28; til₅ = 7 × 5 = 35

Den generelle begrepet denne rekkefølgen er:

til_n = 7n

Og i det andre er det multiplene på 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Så dets generelle begrep er:

Det kan tjene deg: ekte ekte variabel funksjon og dens grafiske representasjon

b_n = 8n

Tilbake til den opprinnelige sammensatte suksessen, tilhører de 35 den første sekvensen, hvis vilkår er til₁, til₂, til₃, til₄ ... 35 er den femte termin, så begrepet som følger må være B₅, som lett oppnås fra regelen for å finne det generelle begrepet:

b₅ = 8 × 5 = 40

Og det er skrevet:

7, 8, 14, 16, tjueen, 24, 28, 32, 35, 40 ..

Eksempler på sammensatte suksesser

Eksempel 1

Du kan lage en sammensatt suksess med geometriske figurer, for eksempel kvadratet og sirkelen, og ordne dem som vist nedenfor:

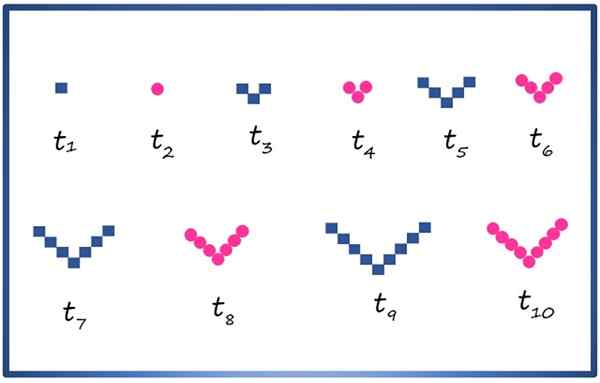De første 10 begrepene i en sammensatt suksess med de firkantede geometriske elementene og sirklene. Kilde: f. Zapata

Hvert begrep er betegnet med t₁, t₂, t₃, t₄ ..., vilkårene for parque -indeks består av sirkler og de med merkelige indekser, firkanter. Å nøye observere sekvensen er det mulig å vite for eksempel at begrepet t_elleve, som ikke vises i bildet, består av 11 firkanter med bestemmelsen i V.

Eksempel 2

Følgende sammensatte suksess består av symboler, i dette tilfellet, bokstavene R og S:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSS ..

Hver nye begrep er bygget ved å legge til et brev til forrige. De fire første begrepene i sekvensen som er vist er:

t₁= R ; t₂= H.H ; t₃= Rr ; t₄= SSS ..

Og neste begrep som vil vises etter vilkårene som er vist er:

t_elleve= Rrrrrr

Eksempel 3

De tidligere eksemplene viste stigende suksesser, der hver verdi øker på noen måte med hensyn til forrige. Men det trenger ikke alltid å være på denne måten, siden suksessene kan være synkende, det vil si at de har et reduseringsmønster.

Og stigende suksesser kan kombineres med synkende suksesser.

Følgende numerisk rekkefølge er sammensatt:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Det kan skilles inn i to suksesser:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Hva er verdiene som må plasseres i de blanke områdene?

Nøye observerer den første suksessen, oppnås hvert begrep ved å legge 3 til foregående termin. Det er derfor en stigende suksess:

Kan tjene deg: vinkelforskyvning

7 = 4 + 3

10 = 7 + 3

Derfor må du i det første tomme rommet plassere:

10 + 3 = 1. 3

Etter dette er følgende begrep, faktisk:

16 = 13 + 3

Og den som går i det andre blanket er:

16 + 3 = 19

Den andre suksessen er synkende, og det er veldig enkelt å finne de manglende begrepene, siden det observeres at hvert begrep oppnås ved å trekke fra 1 fra forrige periode, derfor:

36, 35, 3. 4, 33, 32..

Til slutt kan du skrive:

4, 36, 7, 35, 10, 3. 4, 1. 3, 33, 16, 32, 19,..

Løste øvelser

Oppgave 1

I rekkefølgen sammensatt av eksempel 3 i foregående avsnitt:

a) Tilhører 29 nevnte suksess?

b) Skriv 10 flere vilkår for denne suksessen

Svar til

Ja det hører hjemme, siden den andre arven er synkende og vilkårene oppnås ved å trekke fra 1 fra forrige periode. På denne måten når den til slutt 29.

Svar b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Merk at noen vilkår gjentas.

Oppgave 2

Finn de manglende begrepene i følgende sammensatte suksess:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Svar

De rare begrepene er skrevet for å få den første suksessen:

100, 115, 130, 145, 160, ..

Det observeres at for å finne hvert begrep, må du legge til 15 til forrige periode, derfor er begrepet som følger på 160 175.

Den andre rekkefølgen består av:

500, 480, 460, 440, 420, ..

Hvert begrep skiller seg fra den forrige til 20, og arven er synkende, derfor er begrepet fulgt på 420 400.

Med denne informasjonen blir ytterligere to vilkår lagt til den opprinnelige sammensatte suksessen, som dette:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Referanser

1. Larson, r. (2012). Forkalkning. 8. Utgave. Cengage Learning.
2. Stewart, J. (2007). Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
3. Sammensatte suksesser. Gjenopprettet fra: Media.Educacioncampeche.Gob.MX.
4. Numeriske suksesser. Hentet fra: Matemathweb.com.
5. Suksesser. Aritmetiske og geometriske fremskritt. Hentet fra: MacMillanEducation.er.