Sum av Riemann -historie, formler og egenskaper, øvelser

De Riemann sum Det er navnet som mottar omtrentlig beregning av et definert integral, ved hjelp av en diskret sum med et begrenset vilkårsnummer. En vanlig applikasjon er tilnærmingen til funksjonsområdet i en grafisk.

Det var den tyske matematikeren Georg Friedrich Bernhard Riemann (1826-1866) som for første gang tilbød en streng definisjon av integralen til en funksjon i et gitt intervall. Han kunngjorde det i en artikkel publisert i 1854. 

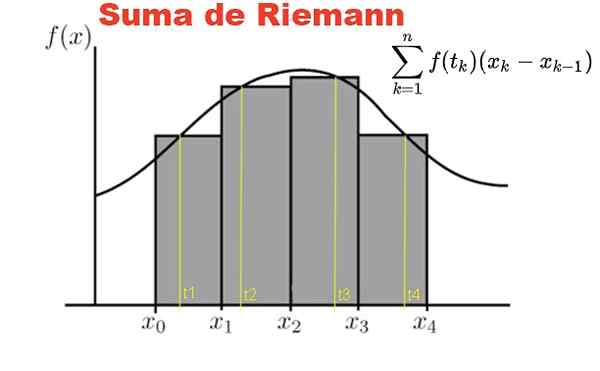
Figur 1. Riemanns sum er definert på en F -funksjon og en partisjon i intervallet [x0, x1]. Kilde: Fanny Zapata.

Riemanns sum er definert på en y = f (x) funksjon, med x som tilhører det lukkede intervallet [a, b]. På dette intervallet er det laget en partisjon p av n elementer:

P = x₀= a, x₁, x₂,..., x_n= B

Dette betyr at intervallet er delt som følger:

 Her t_k er mellom x_K-1 og x_k:

x_K-1 ≤ t_k ≤ x_k

Figur 1 viser summen av Riemann for F -funksjonen i intervallet [x₀, x₄] På en partisjon av fire underintervaller, grå rektangler.

Summen representerer det totale arealet for rektanglene, og resultatet av denne summen er numerisk tilnærminger til området under kurven F, blant abscissas x = x₀ y x = x₄.

Selvfølgelig forbedrer tilnærmingen til området under kurven i stor grad i den grad antallet n av partisjoner er større.  På denne måten konvergerer summen til området under kurven, når tallet n Partisjoner har en tendens til uendelig.

[TOC]

Formler og egenskaper

Riemanns sum av F (x) -funksjon på partisjon:

Kan tjene deg: Rhomboid: Kjennetegn, hvordan ta ut omkretsen og området

P = x₀= a, x₁, x₂,..., x_n= B

Definert på intervallet [a, b], er det gitt av:

S (p, f) = ∑_{K = 1}ⁿ f (t_k) (x_k - x_K-1) 

Hvor t_k Det er en verdi i intervallet [x_k, x_K-1]. I summen av Riemann brukes regelmessige intervaller med bredder vanligvis Δx = (b - a)/n, hvor a og b er minimums- og maksimumsverdiene for abscissa, mens n er antall underavdelinger.

I så fall Riemanns høyre sum er:

Sd (f, n) = [f (a+Δx)+f (a+2Δx)+…+f (a+(n-1) Δx)+f (b)]*Δx

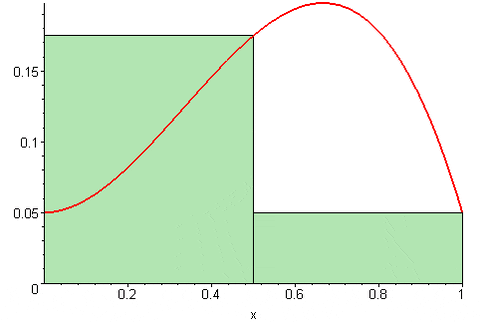Figur 2. Riemanns høyre sum. Kilde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)].

Mens Riemanns venstre sum Det uttrykkes som:

Ja (f, n) = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)]*Δx

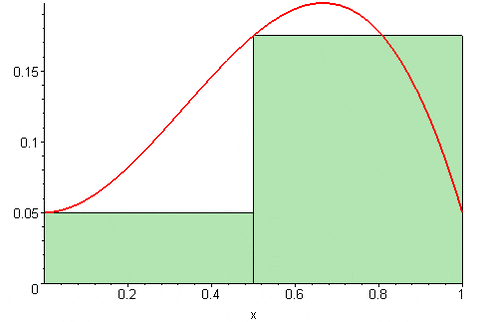Figur 3. Summen av Riemann igjen. Kilde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)]

Endelig Riemann Central Sum er:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+…+f (b- Δx/2)]*Δx

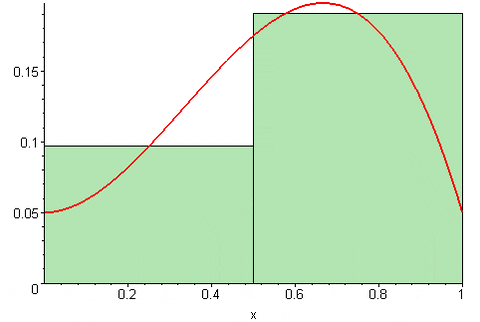Figur 4. Mellomliggende sum av riemann. Kilde: Wikimedia Commons. 09GLASGOW09 [CC BY-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)]

Avhengig av hvor punkt T er lokalisert_k I intervallet [x_k, x_K-1] Riemanns sum kan overvurdere eller undervurdere den nøyaktige verdien av området under y = f (x) funksjonskurve (x). Det vil si at rektanglene kan utmerke seg fra kurven eller være litt under dette.

Området under kurven

Hovedegenskapen til summen av Riemann og som dens betydning blir, er at hvis antallet underavdelinger har en tendens til uendelig, konverterer resultatet av summen til den definerte integreringen av funksjonen:

Det forrige uttrykket tilsvarer definisjonen av Riemanns integral og gjelder forutsatt at F -funksjonen er kontinuerlig og myk. For mer spesielle funksjoner er det andre definisjoner av integralen (Integral de Stieldjes og Integral de Lebesgue).

Det kan tjene deg: Standard estimatfeil: Hvordan det beregnes, eksempler, øvelser

Løste øvelser

- Oppgave 1

Beregn verdien av integralet som er definert mellom A = -2 til B = +2 i funksjonen:

f (x) = x²

Benytt deg av en sum av Riemann. For å gjøre dette, finn summen for vanlige partisjoner av intervallet [a, b] og ta deretter den matematiske grensen for saken at antall partisjoner lagrer til uendelig. 

Løsning

Dette er trinnene å følge:

-For det første er partisjonsintervallet definert som: 

Δx = (b - a)/n. 

-Da er summen av Riemann til høyre som tilsvarer funksjonen f (x) slik:

-Nå erstattes de a = -2 og b =+2, slik at intervallet eller trinnet Δx = 4/n. Det vil si at summen av Riemann for funksjonen f (x) = x² er:

-Da utvikles den firkantede binomialen: 

[-2 +(4i/n)]² = 4 - (16 I /N) + (4 /n)² Yo²

-Og så erstattes den nøye i summen:

-Neste trinn er å skille sammendragene og fjerne de konstante beløpene som en vanlig faktor for hver sum. Det er nødvendig å ta hensyn til at indeksen er jeg, derfor tallene og vilkårene med n De anses som konstante:

-Hver sum blir evaluert, siden det for hver av dem er passende uttrykk. For eksempel den første av sammendragene da n:

Det andre er:

 Og den tredje er:

 -Erstatte resultatene av sammendragene i summen av Riemann, oppnås endelig det:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Endelig må du beregne integralen er:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5.333

Leseren kan bekrefte at dette er det nøyaktige resultatet, som kan oppnås ved å løse det ubestemte integralet og evaluere integrasjonsgrensene med Barrow -regelen.

Kan tjene deg: Hvordan konvertere fra km/h a m/s? Løste øvelser

- Oppgave 2

Bestem omtrent området under funksjonen: 

f (x) = (1/√ (2π) e^(-x2/2)

Mellom x = -1 og x =+1 ved å bruke en sentral sum av Riemann med 10 partisjoner. Sammenlign med det nøyaktige resultatet og estimer den prosentvise forskjellen.

Løsning

Trinnet eller økningen mellom to påfølgende diskrete verdier er:

Δx = (1 - (-1)/10 = 0,2

Slik at P -partisjonen som rektanglene er definert på er slik:

P = -1,0; -0,8; -0,6; -0.4; -0,2; 0,0; 0.2; 0,4; 0,6; 0,8; 1.0

Men som det du ønsker er den sentrale summen, vil funksjonen f (x) bli evaluert i midten av punktene til underintervallene, det vil si i settet:

T = -0.9; -0,7; -0,5; -0,3; -0,1; 0.1; 0.3; 0,5; 0,7; 0,9.

Riemanns sum (sentral) er slik:

S = F (-0,9)*0,2 +F (-0,7)*0,2 +F (-0,5)*0,2 +… +F (0,7)*0,2 +F (0,9)*0,2

Siden F -funksjonen er symmetrisk, er det mulig å redusere summen til bare 5 termer, og resultatet multipliseres med to:

S = 2*0,2*F (0,1)+ F (0,3)+ F (0,5)+ F (0,7)+ F (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funksjonen gitt i dette eksemplet er ingen ringere enn den velkjente Gauss Bell (normalisert, med gjennomsnittlig lik null og standardavvik en). Det er kjent at området under kurven i intervallet [-1,1] for denne funksjonen er 0,6827.

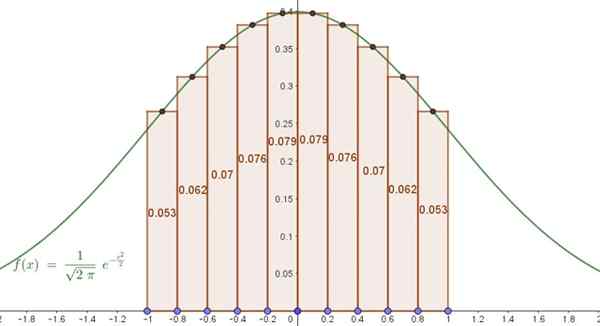Figur 5. Område under en omtrentlig Gauss Bell ved hjelp av en sum av Riemann. Kilde: f. Zapata.

Dette betyr at den omtrentlige løsningen med bare 10 vilkår sammenfaller med den nøyaktige løsningen opp til tre desimaler. Prosentvis feil mellom omtrentlig integral og den nøyaktige er 0,07%.

Referanser

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Omfattende beregning (illustrert ED.). Madrid: ESIC -redaksjon.
2. Unican. Historien om begrepet integral. Gjenopprettet fra: depot.Unican.er
3. UIS. Riemann summerer. Gjenopprettet fra: Matematikk.UIS.Edu.co
4. Wikipedia. Riemann sum. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Integrering av Riemann. Gjenopprettet fra: er.Wikipedia.com