Sum av vektorer grafisk metode, eksempler, løste øvelser

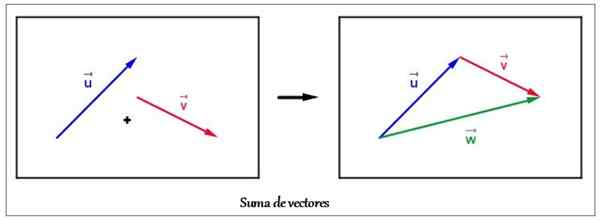
De sum av vektorer Det er tilleggsoperasjonen mellom vektorer som resulterer i en annen vektor. Vektorer er preget av å ha størrelse, og også retning og mening. Derfor er det generelt ikke mulig å legge dem til som det ville bli gjort med skalare mengder, det vil si å legge til tall.

Vektoren oppnådd fra summen av flere vektorer kalles resulterende vektor. I mekanikk snakker vi om resulterende kraft, som er vektorsummen til alle krefter på et legeme. Dette resultatet tilsvarer settet eller styrkenes system.

For å spesifisere sumvektoren fullstendig, er det nødvendig å indikere størrelsen og enhet, retning og mening.

Det er viktig å fremheve at ved å legge til vektorer, må disse representere den samme fysiske størrelsen, derfor er vektorsummen en homogen operasjon. Dette betyr at vi kan legge til en styrke med en annen, men ikke en styrke med en forskyvning, siden resultatet er meningsløst.

Flere metoder er tilgjengelige for å finne den resulterende vektoren: grafikk og analyse. For å finne vektorsummer med grafiske metoder, er det basert på en enkel representasjon for en vektor, nemlig et segment orientert eller pil som dette:

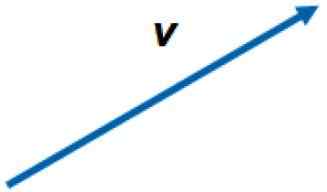Grafisk representasjon av en vektor i planet. Kilde: f. Zapata.

Vektorene er betegnet med svarte bokstaver i trykt tekst, eller med en pil over bokstaven, for å skille dem fra deres respektive størrelser eller av skalare mengder. For eksempel størrelsen på vektoren v Det er ganske enkelt v.

[TOC]

Grafisk metode for å legge til vektorer

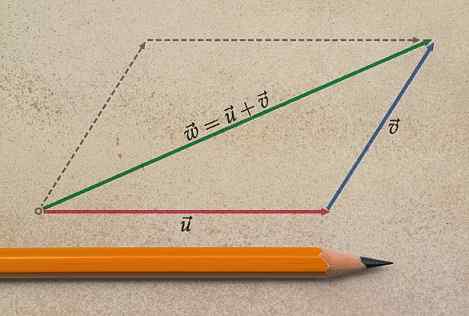
For å legge til mer enn to koblingsvektorer, Polygon -metode enten Polygon, som består av å overføre seg til hver av de adresserte vektorene. Et kjennetegn ved vektorene er at de er ufravikelige når det gjelder oversettelsen, derfor vil vi bruke denne egenskapen til å etablere summen.

Kan tjene deg: termisk utvidelse

Det begynner med noen av vektorene, siden vektortilsetningen er kommutativ og rekkefølgen på tilleggene ikke endrer summen. Den andre vektoren beveger seg nedenfor, og samsvarer med opprinnelsen med slutten av den første.

Deretter blir den brakt til neste vektor og deretter sett den samme prosedyren, som er å matche opprinnelsen med slutten av den forrige. Vi fortsetter på denne måten for å plassere den siste vektoren.

Den resulterende vektoren er den som blir med opprinnelsen til den første med den frie enden av den siste. Navnet på denne metoden kommer fra figuren som resulterer: en polygon.

Eksempel

Sumeksempel på to vektorer i planet med den grafiske metoden. Kilde: Wikimedia Commons

La oss som et eksempel summen av to vektorer eller og v som er vist i det øvre figuren.

Begynner med vektoren eller, Han flyttet til vektoren v For å matche opprinnelsen med slutten av den første. Den resulterende vektoren W Det er trukket fra opprinnelsen til eller til slutten av v, danner en tre -sidig figur: en trekant. Det er grunnen til at i dette spesielle tilfellet kalles prosedyren Trekantmetode.

Legg merke til en viktig detalj, størrelsen eller modulen til den resulterende vektoren er ikke summen av modulene til tilleggsvektorene. Faktisk er det nesten alltid mindre, med mindre vektorene er parallelle.

La oss se nedenfor hva som skjer i dette tilfellet.

Spesiell sak: Summen av parallelle vektorer

Den beskrevne metoden kan også brukes på det spesielle tilfellet der vektorer er parallelle. Tenk på følgende eksempel:

Kan tjene deg: Boltzmann konstant: Historie, ligninger, beregning, øvelserSum av parallelle vektorer. Kilde: f. Zapata.

Vektoren er igjen v I sin opprinnelige posisjon, og flytter til vektoren eller på en slik måte at opprinnelsen stemmer overens med slutten av  v. Nå er en vektor trukket fra opprinnelsen til v Og slutten av eller.

Dette er den resulterende vektoren W og størrelsen er summen av størrelsene på annonsene. Retningen og retningen til de tre vektorene er den samme.

Den resulterende vektoren har en maksimal modul hvis addorene danner en vinkel på 0º, slik som eksemplet. Hvis vektorene danner en vinkel på 180º med hverandre, har den resulterende vektoren en minimumsmodul.

Eksempler på sum av vektorer

- Forskyvninger

En syklist reiser de første 3 km på vei nordover og deretter 4 km vest. Din forskyvning, som vi kaller R, Det finnes lett med trekantmetoden pluss et referansesystem, der kardinalpunkter er merket:

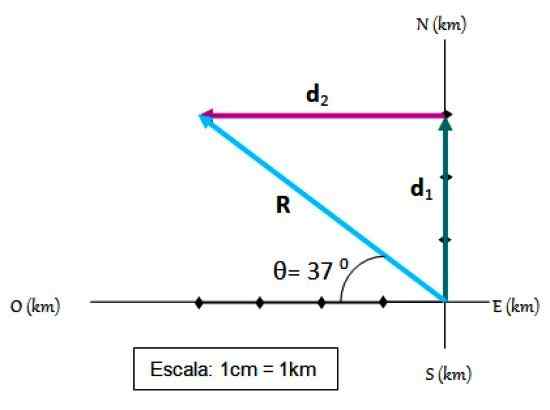Som følge av to forskyvninger. Kilde: f. Zapata.

Trinn for å legge til vektor

-Utgangspunktet sammenfaller med opprinnelsen til referansesystemet.

-På koordinataksene er det valgt en skala, som i dette tilfellet er 1 cm = 1 km

-Den første forskyvningen er tegnet på skala d_1.

-Deretter en d₁ Den andre forskyvningen trekkes d₂, Også på skala.

-Den resulterende forskyvningen R Det er en vektor som går fra opprinnelsen til slutten av d₂.

-Størrelsen til R Det måles med en gradert regel, det er enkelt å bekrefte at r = 5.

-Endelig vinkelen som R Form med horisontalt måles ved hjelp av en transportør og viser seg å være θ = 37 ⁰

- Resulterende hastighet

En svømmer ønsker å krysse en elv, og for dette er ingenting i en hastighet på 6 km/t, vinkelrett på kysten, men en strøm som bærer hastighet på 4 km/t avviker den.

Det kan tjene deg: Ohm: Motstandstiltak, eksempler og trening løst

For å kjenne dens resulterende hastighet, blir svømmerhastighetsvektorene lagt til, som er tegnet vertikal og strøm, som er horisontalt.

Etter den grafiske metoden oppnås den resulterende hastigheten v_R:

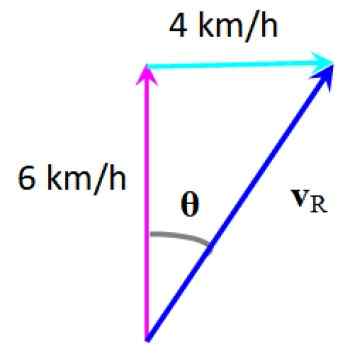Resulterende hastighet. Kilde: f. Zapata.

Avviket som svømmeren opplever kan beregnes av:

θ = arctg (4/6) = 33.7. til høyre for din første adresse

Størrelsen på hastigheten økes fordi elvenes hastighet tilfører vektorly. Du kan finne en skala nøye, som i forrige eksempel.

Eller ved hjelp av de trigonometriske grunnene til 33.7.:

Sen 33.7. = 4/V_R

v_R = 4/ sin 33.7. = 7.21 km/t

Trening løst

På en partikkel Act Follow Forces Act, hvis størrelser er listet opp nedenfor:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Finn den resulterende styrken.

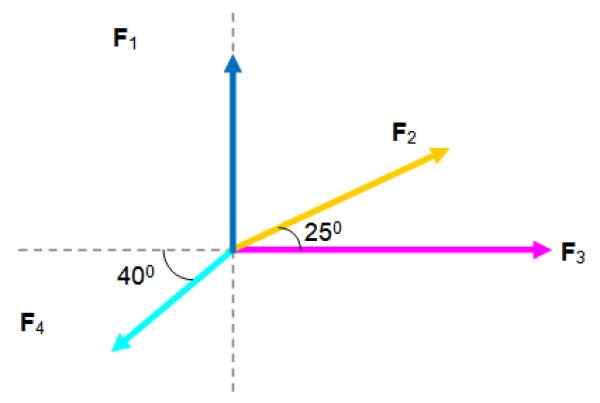Coplanar Forces System. Kilde: f. Zapata.

Løsning

Vi kan legge til grafisk å starte med noen av vektorene, siden vektorsummen er kommutativ.

I figur A begynte med F₁. Etablere en skala og ved hjelp av regel og tropp blir de andre vektorene overført for å plassere dem etter hverandre.

Vektoren F_R er rettet fra opprinnelsen til F₁ til slutten av F₄. Størrelsen er 5.2 n og danner en vinkel på 26.5. med hensyn til horisontalt.

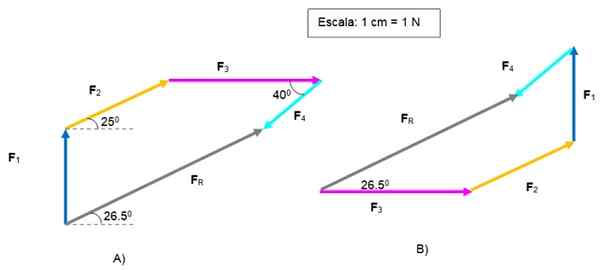Vektor grafisk sum. Kilde: f. Zapata.

I figur B ble det samme problemet løst, og startet med F₃ og slutter med F₄, For å få det samme F_R .

Polygonene er forskjellige, men resultatet er det samme. Leseren kan teste rekkefølgen på vektorene igjen.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.