Teleskopisk sommer hvordan den løses og løste øvelser

De Summering Teleskopisk Det er en gren av operasjoner med numeriske serier. Adresserer sammendragene av elementer fra en innledende verdi til "n" av uttrykk hvis argument skyldes et av følgende mønstre:

(F_x - F_x+1); F_x+1  - F_x)

Hvor det sammendragsuttrykket er definert som følger: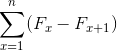

Også:

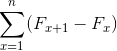
Kilde: Pixabay.com

De representerer en sum av elementer som, når de utvikler, er underlagt kanselleringer av motsatte vilkår. Forårsaker følgende likhet for teleskopiske summeringer:

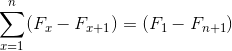
Navnet kommer fra forholdet til utseendet til et klassisk teleskop, som kan brettes og distribueres, noe som endrer dimensjonen betydelig. Tilsvarende kan teleskopiske summeringer, som i sin natur er uendelige, oppsummeres i forenklet uttrykk:

F₁ - F_N+1

[TOC]

Demonstrasjon

Når du utvikler summen av vilkår, er eliminering av faktorer ganske åpenbar. Hvor for hvert av tilfellene vil motsatte elementer vises i følgende iterasjon.

Den første saken vil bli tatt som et eksempel, (f_x - F_x+1), siden prosessen fungerer homolog med (f_x+1-F_x).

Utvikling av de første 3 verdiene 1, 2, 3 Forenklingstiden blir observert

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Hvor ved å uttrykke summen av de beskrevne elementene:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Det observeres at begrepene f₂ og f₃ De beskrives med motsetningene sine, noe som gjør deres forenkling uunngåelig. På samme måte observeres det at begrepene f₁ og f₄ forbli.

Hvis summen ble laget av x = 1 til x = 3, betyr det at element f₄ tilsvarer det generiske begrepet f_N+1.

Dermed demonstrere likhet:

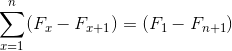
Hvordan løses det?

Hensikten med teleskopiske summeringer er å lette arbeidet, slik at det ikke er nødvendig å utvikle en uendelig mengde vilkår, eller forenkle noen for lang kjede.

Kan tjene deg: Trachtenberg -metode: Hva er det, eksempler

For oppløsning vil det bare være nødvendig å evaluere vilkår F₁ og f_N+1. Disse enkle erstatningene utgjør det endelige resultatet av summen.

Totaliteten av vilkårene vil ikke bli uttrykt, og blir nødvendig for demonstrasjonen av resultatet, men ikke for den normale beregningsprosessen.

Det viktige er å legge merke til konvergensen av den numeriske serien. Noen ganger vil ikke summen bli uttrykt på en teleskopisk måte. I disse tilfellene er implementeringen av alternative faktoriseringsmetoder veldig vanlig.

Den karakteristiske faktoriseringsmetoden i teleskopiske sammendrag er den av enkle fraksjoner. Dette skjer når en original fraksjon dekomponerer til en sum av flere brøk, der det teleskopiske mønsteret kan observeres (f_x - F_x+1) eller (f_x+1  - F_x).

Nedbrytning i enkle brøk

For å bekrefte konvergensen av numeriske serier, er det veldig vanlig å transformere rasjonelle uttrykk med den enkle fraksjonsmetoden. Målet er å modellere argumentet til formen for en teleskopisk summering.

For eksempel representerer følgende likhet en nedbrytning i enkle brøk:

Når du utvikler den numeriske serien og bruker de tilsvarende egenskapene, tar uttrykket som følger:

Der den teleskopiske formen kan sees (f_x - F_x+1).

Prosedyren er ganske intuitiv og består i å finne verdiene til telleren som uten å bryte likheten, tillate å skille produktene som er i nevneren. Ligningene som oppstår i bestemmelsen av disse verdiene, blir hevet i henhold til sammenligninger mellom begge sider av likhet.

Denne prosedyren blir observert trinn for trinn i utviklingen av trening 2.

Kan tjene deg: 6 morsomme matematiske gåter for barn

Historie

Det er ganske usikkert å kunne definere det historiske øyeblikket der de teleskopiske summeringene ble presentert. Imidlertid begynner implementeringen å bli sett i det syttende århundre, i numeriske seriestudier utført av Leibniz og Huygens.

Begge matematikerne, når de utforsker summeringene av trekantede tall, begynner å legge merke til trender i konvergensen av visse serier med påfølgende elementer. Men enda mer interessant er begynnelsen på modelleringen av disse uttrykkene, i elementer som ikke nødvendigvis skjer.

Faktisk har uttrykket tidligere brukt til å referere til enkle brøk:

Det ble presentert av Huygens og ble umiddelbart kalt Leibniz's oppmerksomhet. Som over tid kan observere konvergens til verdi 2. Uten å vite det, implementerte det den teleskopiske summeringen.

Øvelser

Oppgave 1

Definer hvilket begrep følgende sum konvergerer:

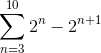
Når summen er utviklet manuelt, observeres følgende mønster:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶) ... (2¹⁰ - 2^elleve)

Hvor faktorene fra 2⁴ opptil 2¹⁰ De presenterer positive og negative deler, noe som gjør avbestillingen deres tydelig. Da vil de eneste faktorene som ikke vil bli forenklet være den første “2³"Og den siste" 2^elleve"".

På denne måten, ved implementering av de teleskopiske sammendragskriteriene, oppnås det:

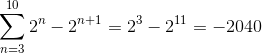
Oppgave 2

Transformer argumentet til en sum av teleskopisk type og definer konvergensen av serien:

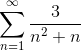
Som antydet i uttalelsen, vil det første være å dekomponere i enkle brøk, for å revurdere argumentet og uttrykke det i en teleskopisk form.

2 fraksjoner hvis nevner er henholdsvis "n" og "n+1" må finnes, der metoden som brukes nedenfor må oppnå verdiene til telleren som oppfyller likhet.

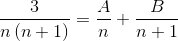
Verdiene til A og B er definert. Første sum av brøk er laget.

Kan tjene deg: 60 deling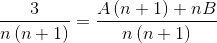

Deretter er nevnerne forenklet og en lineær ligning etableres.

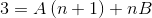
I neste trinn blir uttrykket av høyre operert, inntil et mønster som kan sammenlignes med “3” til venstre.

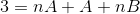
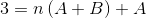
For å definere ligningene som skal brukes, må resultatene fra begge sider av likhet sammenlignes. Det vil si at ingen variable n -verdier blir observert på venstre side, på denne måten må a +b være lik null.

A + b = 0; A = -b

På den annen side vil den konstante verdien måtte være lik konstant verdi 3.

A = 3

Derfor.

A = 3 og b = -3

Allerede definert verdiene til telleren for enkle brøk, summen tenker på nytt.

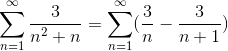
Der den generiske formen for teleskopisk summering allerede er oppnådd. Den teleskopiske serien er utviklet.

Hvor ved å dele med et veldig stort antall, vil resultatet omgås mer og mer, og observere konvergensen av serien til Value 3.

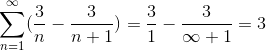
Denne typen serier kunne ikke løses med andre ord, på grunn av den uendelige mengden iterasjoner som definerer problemet. Imidlertid rammer denne metoden sammen med mange andre grenen av studien av den numeriske serien, hvis mål er å bestemme konvergensverdiene eller definere divergensen i disse seriene.

Referanser

1. Infinitesimale beregningstimer. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Omfattende beregning: Successions and Series of Functions. Antonio Rivera Figueroa. Patria Editorial Group, 21. oktober. 2014.
3. Et kurs i kalkulus og reell analyse. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5. juni. 2006.
4. Uendelig serie. Tomlinson Fort. Clarendon Press, 1930.
5. Elementer i teorien om uendelige prosesjoner. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.