Molekylær kinetisk teorihistorie, postulater og eksempler

De Molekylær kinetisk teori Det er en som søker å forklare de eksperimentelle observasjonene av gasser fra et mikroskopisk perspektiv. Det vil si at den prøver å knytte arten og oppførselen til gassformige partikler, med de fysiske egenskapene til gass som væske; Forklar makroskopikken fra det mikroskopiske.

Gasser har alltid vært gjenstand for interesse for forskere på grunn av deres egenskaper. De okkuperer hele volumet av beholderen de er i, kan komprimere helt uten at innholdet deres motsetter seg den lavere motstanden; Og hvis temperaturen øker, begynner beholderen å utvide seg, og kan til og med sprekke.

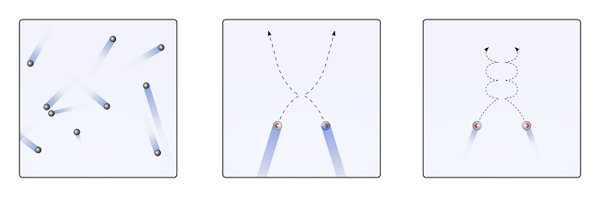Gassformede partikler under fjerne forhold eller nær flukt. Kilde: Olivier Cleynen og bruker: Sharayanan [CC BY-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)]

Mange av disse egenskapene og atferden er oppsummert i lovene til ideelle gasser. Imidlertid anser de gass som en helhet og ikke som et sett med millioner av spredte partikler i rommet; I tillegg gir den ikke, fra trykk, volum og temperaturdata, mer informasjon om hvordan disse partiklene beveger seg.

Det er slik at den molekylære kinetiske teorien (TCM) foreslår å visualisere dem som mobile sfærer (overlegen bilde). Disse kulene kolliderer med hverandre og veggene vilkårlig, og opprettholder en lineær bane. Men når temperaturen avtar og trykket øker, blir banen til kulen kurve.

En gass, ifølge TCM, må oppføre seg som sfærene i den første bildeboksen. Men når de er avkjølt og øker trykket på dem, beveger oppførselen seg bort fra idealet. De er da ekte gasser, nær flytning og går til væskefasen.

Under disse forholdene blir interaksjonene mellom kulene viktigere, til det punktet at hastighetene deres øyeblikkelig er sakte. Jo nærmere de er fra flytningen, jo flere kurver blir banen deres (høyre boks), og kollisjonene deres er mindre energi.

[TOC]

Historie

Daniel Bernoulli

Ideen om disse områdene, bedre kalt atomer, hadde allerede blitt vurdert av den romerske filosofen Lucretius; Ikke for gasser, men for faste, statiske gjenstander. På den annen side, i 1738 påførte Daniel Bernoulli atomvisjonen på gasser og væsker ved å forestille seg dem som uordnede kuler som beveget seg i alle retninger.

Hans arbeid brøt imidlertid fysikkens lover på den tiden; En kropp kunne ikke bevege seg for alltid, så det var umulig å tro at et sett med atomer og molekyler kolliderte med hverandre uten tap av energi; det vil si at eksistensen av elastiske kollisjoner ikke var mulig.

Rudolf Clausius

Et århundre senere forsterket andre forfattere TCM med en modell der gasspartikler beveget seg i en retning. Rudolf Clausius kompilerte imidlertid resultatene og bevæpnet en mer fullstendig modell av TCM som den forsøkte å forklare de ideelle gase -lovene som ble demonstrert av Boyle, Charles, Dalton og Avogadro.

Kan tjene deg: Coulombimetry: grunnleggende, typer, applikasjoner

James Clerk Maxwell og Ludwig Boltzmann

I 1859 uttalte James Clerk Maxwell at gassformede partikler viser en rekke hastigheter ved en gitt temperatur, og at et sett med dem kan vurderes ved hjelp av en gjennomsnittlig molekylhastighet.

Da koblet Ludwig Boltzmann i 1871 eksisterende ideer med entropi, og hvordan termodynamisk alltid har en tendens til å okkupere maksimal mulig plass på en homogen og spontan måte.

Postulat molekylær kinetisk teori

Å vurdere gass fra partiklene, en modell der visse postulater eller forutsetninger er oppfylt; postulert som logisk skal kunne forutsi og forklare (så trofast som mulig) de makroskopiske og eksperimentelle observasjonene. Når det er sagt, er Postulatene til TCM nevnt og beskrevet.

Volumet av gassformige partikler er ubetydelig

I en beholder full av gassformede partikler sprer de seg og beveger seg bort mellom dem gjennom alle hjørner. Hvis de for et øyeblikk alle kunne møtes på et bestemt punkt i beholderen, uten flytende.

Det betyr at selv om den inneholder millioner av gassformede partikler i beholderen, er den egentlig mer tom enn full (volum-vacío-forhold mye mindre enn 1); Derfor, hvis barrierer tillater det, kan han og gass inni komprimeres brått; siden partiklene er veldig små, akkurat som volumet.

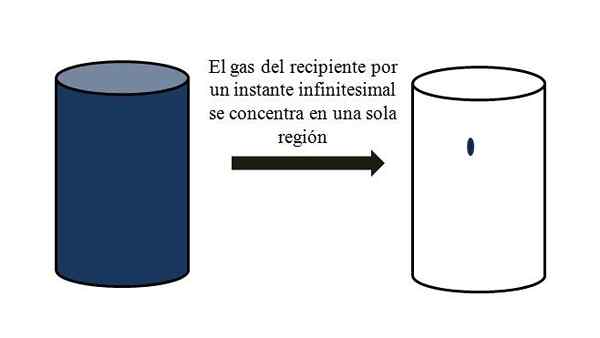Volum-vacío forhold til en gass i en beholder. Kilde: Gabriel Bolívar.

Det overlegne bildet illustrerer nettopp hva som er kommentert ovenfor, ved hjelp av en blåaktig gass.

Attraksjonskreftene mellom partiklene er null

Gassformede partikler inne i beholderen kolliderer med hverandre uten tilstrekkelig tid til at interaksjonene deres skal bli styrke; Enda mindre når det som hovedsakelig omgir dem er molekylær tomt. En umiddelbar konsekvens av dette er at deres lineære baner lar dem dekke beholderens volum fullstendig.

Hvis ovennevnte ikke var slik, ville en "bisarr" og "labyrint" beholder ha våte regioner som et resultat av gasskondensasjon; I stedet reiser partiklene hele beholderen med full frihet, uten styrken av interaksjonene deres som stopper dem.

Kan tjene deg: klorsyre (Hclo3) Disposser av gassformige partikler når interaksjonene er null eller ubetydelige (til., lineær), og når de er viktige (b., kurver). Kilde: Gabriel Bolívar.

De lineære banene til det øvre bildet (a.) demonstrere dette postulatet; Mens hvis banene er kurver (b.), bevis på at det er interaksjoner som ikke kan ignoreres mellom partiklene.

Gassformede partikler er alltid i bevegelse

Fra de to første postulatene konvergerer i tillegg det faktum at gasspartikler aldri slutter å bevege seg. Når de er uskarpe i beholderen, kolliderer de med hverandre og med veggene av det samme, med en kraft og hastighet som er direkte proporsjonal med den absolutte temperaturen; Denne kraften er, presset.

Hvis gassformede partikler slutter å bevege seg et øyeblikk, ville det bli vitne til i "røykspråk", som oppstår fra ingenting, med nok tid til å bestille seg selv i et vakuum og gi tilfeldige måter.

Kollisjonene mellom partiklene og veggene i beholderen er elastiske

Hvis de elastiske kollisjonene mellom de gassformede partiklene og veggene i beholderen aldri vil forekomme i beholderen, vil den aldri forekomme (mens de fysiske forholdene ikke endrer) kondensasjonen av gassen; eller hva som er det samme som å si at de aldri hviler, og at de alltid kolliderer.

Dette er fordi det i elastiske kollisjoner ikke er noe nettotap av kinetisk energi; En partikkel kolliderer med veggen og spretter i samme hastighet. Hvis en partikkel når kollisjonen reduserer hastigheten, akselererer den andre, uten varme eller lyd som forsvinner den kinetiske energien til noen av dem.

Kinetisk energi forblir ikke konstant

Partiklene er bevegelse tilfeldig og kaotisk, slik at ikke alle bærer samme hastighet; Som skjer, for eksempel på en motorvei eller i en mengde. Noen er mer energiske og reiser mer fart, mens andre er trege og venter på at en kollisjon skal akselerere dem.

For å beskrive hastigheten din er det da nødvendig å beregne et gjennomsnitt; Og med dette oppnås den gjennomsnittlige kinetiske energien til partiklene eller gassmolekylene. Ettersom den kinetiske energien til alle partikler stadig endres, tillater gjennomsnittet bedre datakontroll, og du kan jobbe med større pålitelighet.

Gjennomsnittlig kinetisk energi er lik en gitt temperatur for alle gasser

Gjennomsnittlig molekylær kinetisk energi (EC_MP) I en beholder er den modifisert med temperaturen. Ved høyere temperatur vil denne energien være større. Fordi det er et gjennomsnitt, kan det være partikler eller brus som har større eller mindre energi med hensyn til denne verdien; Noe raskere og mer treg, henholdsvis.

Kan tjene deg: syrer og baser: forskjeller, egenskaper, eksempler

Matematisk kan det demonstreres at EC_MP Det avhenger utelukkende av temperaturen. Dette betyr at det ikke spiller noen rolle hva gassen, dens molekylmasse eller struktur, dens EC_MP Det vil være det samme ved en T -temperatur og vil bare variere hvis det øker eller synker. Av alle postulater kanskje dette er det mest relevante.

Og hva med den gjennomsnittlige molekylhastigheten? I motsetning til EC_MP, Molekylmasse påvirker hastigheten. Jo tyngre partikkel eller gassmolekyl, det er naturlig å forvente å bevege seg saktere.

Eksempler

Nedenfor er noen korte eksempler på hvordan TCM har klart å gi forklaringer til lovene om ideelle gasser. Selv om de ikke blir adressert, kan andre fenomener, som formidling og utstrømning av gasser, også forklares med TCM.

Boyle Law

Hvis volumet på beholderen komprimeres ved konstant temperatur, reduseres avstanden som gasspartiklene må kollidere for å kollidere mot veggene; som er lik en økning i hyppigheten av disse kollisjonene, noe som resulterer i større trykk. Når temperaturen er konstant, EC_MP Det er også konstant.

Charles Law

Hvis T, EF øker_MP vil øke. Gassepartikler vil bevege seg raskere og kollidere et større antall ganger med veggene i beholderen; øker trykket.

Hvis veggene er fleksible, i stand til å utvide, vil området bli større og trykket vil falle til det blir konstant; Og som et resultat vil volumet også øke.

Daltons lov

Hvis flere liter med forskjellige gasser ble tilsatt i en romslig beholder, fra mindre beholdere, ville deres totale indre trykk være lik summen av delvis trykk som utøves av hver type gass hver for seg.

Fordi? Fordi alle gasser begynner å kollidere med hverandre og spre homogent; Interaksjonene mellom dem er ugyldige, og vakuumet dominerer i beholderen (postulater av TCM), så det er som om hver gass er funnet alene, og utøver trykket på en individuelt måte uten forstyrrelse av de andre gassene.

Referanser

1. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning, s 426-431.
2. Fernández Pablo. (2019). Molekylær kinetisk teori. Vix. Gjenopprettet fra: VIX.com
3. Jones, Andrew Zimmerman. (7. februar 2019). Kinetisk molekylær teori om gasser. Gjenopprettet fra: Thoughtco.com
4. Hall Nancy. (5. mai 2015). Kinetisk teori om gasser. Glenn Research Center. Hentet fra: GRC.gryte.Gov
5. Blaber m. & Nedre s. (9. oktober 2018). Grunnleggende om kinetisk molekylær teori. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org
6. Den kinetiske molekylære teorien. Hentet fra: Chemed.Chem.Purdue.Edu
7. Wikipedia. (2019). Kinetisk teori om gasser. Hentet fra: i.Wikipedia.org
8. Toppr. (s.F.). Kinetisk molekylær teori om gasser. Gjenopprettet fra: Toppr.com