Molekylær orbital teori

Hva er molekylær orbital teori?

De Molekylær orbital teori (Tom) Det er en matematisk modell utviklet for å forklare de fysisk -kjemiske egenskapene til molekyler, for eksempel absorpsjon og utslipp av stråling, elektrisk ledningsevne, så vel som den elektroniske naturen til koblingene. Dette vurderer, i motsetning til Valencia Link Theory (TEV), at elektroner flyttes gjennom molekylet, uten å være sannsynlig lokalisert i lenkene.

Derfor bruker molekylær orbitalteori de samme kvanteprinsippene som dikterer bølgefunksjonene for atomiske orbitaler, og beskriver dermed energitilstanden til elektroner i atomer; Først nå, adresserer de så -kallede molekylære orbitalene, stammer fra de lineære kombinasjonene av atombanene til atomene som er koblet.

Paramagnetismen av flytende oksygen, og derfor attraksjonen for magneter, blir forklart takket være den molekylære orbitalteorien. Kilde: Pieter Kuipeper via Wikipedia.

Den molekylære orbitalteorien fungerer da, og arbeider med molekylære orbitaler, deres elektroniske og romlige fordelinger, så vel som diagrammer av deres respektive energier, som tillater å observere energigapene som skiller dem. Fremfor alt forklarer paramagnetismen til visse stoffer, for eksempel molekylært oksygen i flytende tilstand (se over).

O₂, Beskrevet av Lewis strukturer og Valencias koblingsteori, har den alle sammenkoblede elektroner, så i teorien skal den være diamagnetisk. Imidlertid har det i praksis blitt vist at det faktisk er paramagnetisk, det vil si at den mangler elektroner; Spesielt et par manglende elektroner.

Fra konstruksjonen av OM -diagrammet (molekylære orbital) for o₂, Et homonukleært diatomisk molekyl, det kan sees at det faktisk vil være to høy -energi manglende elektroner. Ikke bare dette, men spinnet og plasseringen av disse elektronene i OMS forklarer også andre elektroniske tilstander i OR₂ (enkelt).

Andre av de viktigste triumfer av molekylær orbital teori er at det hjelper med å forutsi mulig eksistens av diatomiske molekyler, så vel som deres relative stabilitet. Dermed er molekylær orbital teori rett i prediksjon av molekyler som B₂ og Li₂, Selv når de bare kan oppdage i dampfasen ved høye temperaturer. Også denne teorien avviser eksistensen av det hypotetiske jeg har₂ eller ne₂.

Typer molekylære bindinger og orbitaler

Som med Valencia Link Theory, vurderes i den molekylære orbitalteorien, flere typer koblinger, avhengig av retningen til overlappingen av atomiske orbitaler som deltar i den kjemiske bindingen. Blant de viktigste og til stede i molekylær natur har vi Sigma- og PI -bindinger.

Sigma

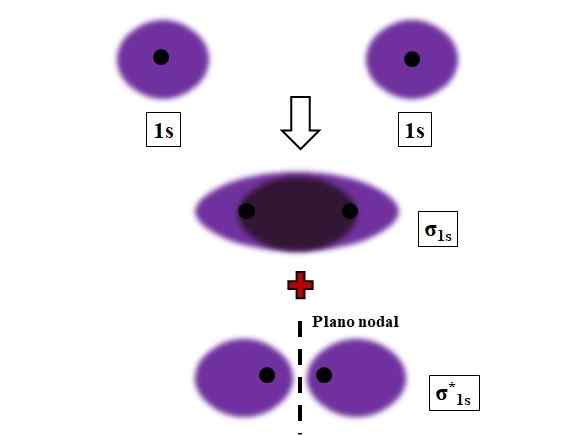Dannelse av σ1s og σ1s* koblinger under overlappingen av to atombaner 1s. Kilde: Gabriel Bolívar.

Sigma, σ -bindinger er etablert når atombaner overlapper fronten, i forhold til en tenkt internukleær øks.

Tenk for eksempel σ -koblingen som dannes når to 1s atombaner, ifølge et hydrogenatom, er nær veldig kort avstand (bilde over). Fordi 1s orbitaler er symmetriske, vil overlappingen alltid være frontal; Derfor vil de alltid generere molekylære orbitaler σ_1s og σ_1s*.

Merk nå som molekylær orbital σ_1s viser en elektronisk tetthet konsentrert i rommet som skiller de to kjernene. Dette betyr at i en orbital σ_1s Sannsynligheten for å finne et elektron er maksimalt i dette området av molekylet. Elektronene til σ_1s De flyttes gjennom hele plassen som dekker den lilla fargen.

På den annen side, i orbital σ_1s* Vi har et nodalplan mellom de to kjernene. Dette betyr at sannsynligheten for å finne et elektron mellom det rommet er lik null. Merk at i orbital σ_1s* Elektroner beskriver posisjoner rundt hver av de to kjernene; ikke rundt molekylet som helhet.

Kan tjene deg: radio: struktur, egenskaper, bruk, skaffe

Pi

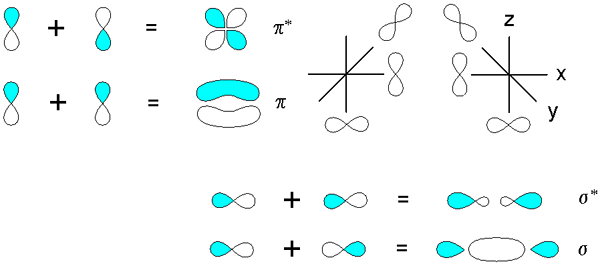Sigma og Pi -obligasjoner avledet fra overlappingen av orbitaler p. Kilde: V8rik på i.Wikipedia, CC BY-SA 3.0, via Wikimedia Commons

Tenk nå på molekylære bindinger og orbitaler. Disse oppstår når overlappingen av orbitalene skjer i en retning vinkelrett på den internukleære aksen, som er vilkårlig festet i noen av aksene til det kartesiske planet. Forutsatt at vi snakker om en 2p orbital_x, 2p orbital_og Det vil være gratis å etablere en PI -lenke (se blå og hvite lober).

Når to orbitaler 2p_og To molekylære orbitaler stammer: π_2py og π_2py*; Den første har den høyeste elektroniske tettheten og under den internukleære aksen, mens den andre ligner en fire -petal blomst, der sannsynligheten for å finne elektroner er mye lavere.

På den annen side, orbitalene 2p, for å si 2p_x, De kan også overlappe hverandre for å stamme en σ -binding og to molekylære orbitaler σ_2px og σ_2px*. Som i tilfellene av σ_1s og σ_1s*, Orbital σ_2px viser større elektronisk tetthet mellom de to kjernene; som er i strid med σ_2px*, der elektroner er orientert mot sidene på utsiden.

Lenke

Linding molekylære orbitaler er de som bidrar til molekylets stabilitet. Det vil si at de må ha mindre energi sammenlignet med atombanene til individuelle atomer før de kobler og danner molekylet. I disse orbitalene flyttes elektronene av alle dimensjonene til molekylet som helhet.

I OM -diagrammer vil disse alltid være lokalisert under atombanene som kombineres for å danne dem. Dette vil bli mer detaljert i de neste seksjonene.

Anti -hut

Anti -Husing Molecular Orbitals, derimot, er de som destabiliserer molekylet. De er symbolisert med en stjerne (*), og energiene deres er høyere enn de atomiske orbitaler som oppsto dem. I disse orbitalene flyttes elektronene ganske uregelmessig, som om molekylet var elektronisk fragmentert.

I OM -diagrammer vil de alltid være lokalisert over atombanene som kombineres for å danne dem.

Ikke koblet

I mellomtiden er ikke -koblende orbitaler, så vel som deres elektroner, de som ikke bidrar eller skader stabiliteten til molekylet. Hans energier er veldig lik de fra atomiske orbitaler.

Lenkeordre

Koblingsrekkefølgen blir i teorien om den molekylære orbitalen, og det samme. Dermed tilsvarer en koblingsrekkefølge lik 1 en enkel lenke (-). Og en koblingsordre (eller.e) lik 2, tilsvarer en dobbeltbinding (=). Så videre.

Denne ordren bestemmes ut fra tellingen av elektroner i OM -diagrammer for et bestemt molekyl. For å gjøre dette, må følgende formel brukes:

enten.E = (antall koblede elektroner - antall anti -hytte -elektroner)/2

Linkelektroner bidrar til molekylet for å stabilisere seg, mens anti -fiery -elektroner destabiliserer det. Derfor, jo mer anti -sungelektroner, jo mindre OR eller.E, og molekylet vil ha en tendens til å være veldig ustabilt. Når o.E er lik 0, det betyr at molekylet ikke eksisterer (eller i det minste i teorien).

Om diagrammer

I OM -diagrammer er energiene til molekylære orbitaler representert, og dens elektroniske fylling er også visualisert, som adlyder reglene for Aufbauf og Sinn, så vel som prinsippet om ekskludering av Pauling. Tenk for eksempel følgende to diagrammer:

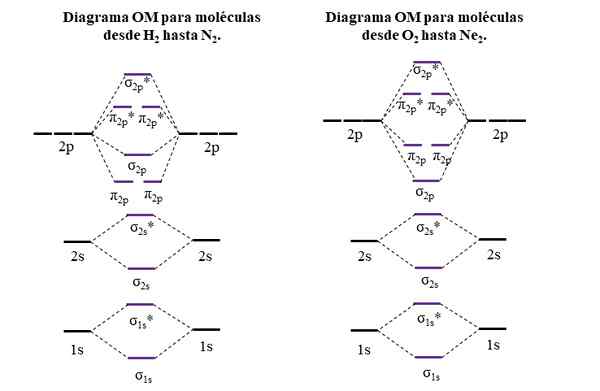OM -diagrammer for molekyler i den første og andre perioden av den periodiske tabellen. Kilde: Gabriel Bolívar.

Horisontale linjer på sidene, svart, representerer energiene til atombaner. I stedet er sentrale horisontale linjer, lilla, energiene til molekylære orbitaler. Legg merke til hvordan koblings- og anti -agent OMS er fordelt (*) i forhold til atombanene til individuelle atomer.

Det kan tjene deg: en aminogruppe (NH2): Struktur, egenskaper, eksempler

Legg også merke til at i riktig diagram, OM σ_{2 s} De endrer sted med π_{2 s}. Dette skjer med molekylene til O₂, F₂, og den hypotetiske NE₂.

Eksempler

I de følgende eksemplene vil OM fortsette med elektronene, beregne koblingsrekkefølgen og komme med spådommer om kraften til bindingen eller stabiliteten til det aktuelle molekylet.

H₂

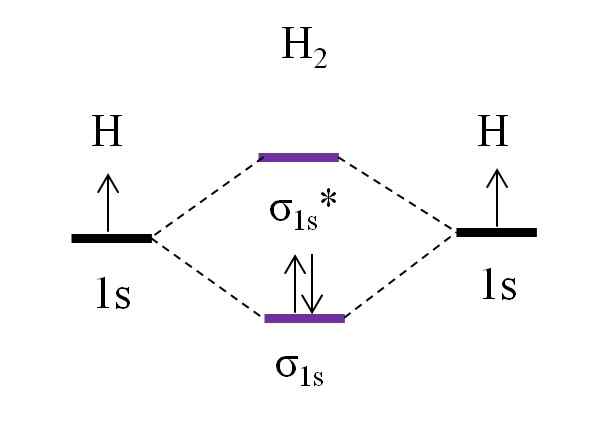Om diagram for dihydrogenmolekyl. Kilde: Gabriel Bolívar.

Starter med det enkleste molekylet, dihydrogen, h₂, To H -atomer er koblet sammen ved å kombinere sine to 1s atombane for å danne to molekylære orbitaler σ_1s og σ_1s*. De to elektronene fortsetter deretter med å fylle de molekylære orbitalene.

Først er orbital σ fylt_1s, Fordi det er minst energi (Aufbauf -regel). Deretter må det andre elektronet avslutte å fylle orbital σ_1s Før klatring av orbital σ_1s* (Synkeregel). Og til slutt guider dette andre elektronet spinnet i motsatt retning av det første elektronet (Pauling Exclusion Principle). Dermed er de to elektronene lokalisert i den koblede orbital σ_1s.

Hva med lenkebestillingen? I lenken molekylær orbital σ_1s Vi har 2 elektroner; Mens du er i anti -hell molekylær orbital σ_1s* Vi har ingen. Derfor ville beregningen være:

enten.E = (2-0)/2

= 1

Å være eller.Og lik 1 betyr det at lenken som forener de to hydrogenatomene er enkel: h-h. Generelt, hvis denne verdien er lik eller større enn 1, sies det at molekylet eksisterer og er stabilt.

Han₂

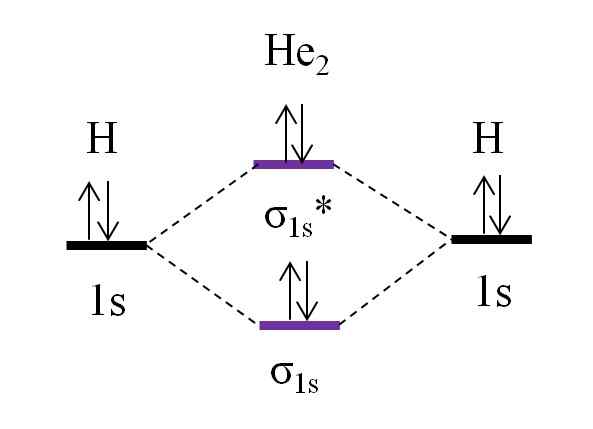Om diagram for hypotetisk dihelio molekyl. Kilde: Gabriel Bolívar.

Anta nå at du har molekylet til han₂. Over ser vi at OM -diagrammet er veldig likt H₂, Med to ekstra elektroner som er lokalisert i orbital σ_1s*. Når det er totalt 4 elektroner som legger til de to atomene, må det også være 4 elektroner i alle de resulterende molekylære orbitalene.

Bestemme o.E for jeg han₂ vi vil ha:

enten.E = (2-2)/2

= 0

Dette betyr at det ikke er noen mulig kobling som de to heliumatomene. Faktisk har til dags dato eksistensen av dette molekylet ikke blitt identifisert, noe som stemmer overens med spådommene om molekylær orbital teori.

B₂

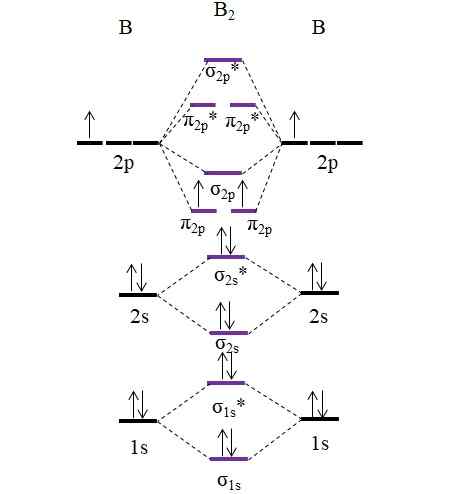OM -diagram for B2 -molekylet. Kilde: Gabriel Bolívar.

Merk at i dannelsen av molekylære orbitaler blir også elektronene til de indre lagene tatt i betraktning; Ikke bare de fra Valencia.

I eksemplet med Diboro -molekylet, B₂, Hvert boratom bidrar med 5 elektroner totalt, hvorav 3 er fra Valencia; Dette er de av deres 2s og 2p orbitaler. De to elektronene i orbitalene 2p er plassert i forskjellige molekylære orbitaler π_{2 s} Med parallelle ryggrader (synkeregel).

Vi fortsetter deretter med å beregne koblingsordren:

enten.E = (6-4)/2

= 1

Derfor forventes molekylet å ha en enkel B-B-lenke. B₂ Det er et molekyl som bare eksisterer i dampstadiet ved veldig høye temperaturer, fordi bor under normale forhold vedtar mer komplekse nettverksstrukturer og design.

C₂ og c₂^2-

Tenk først OM -diagrammet for molekyl C₂:

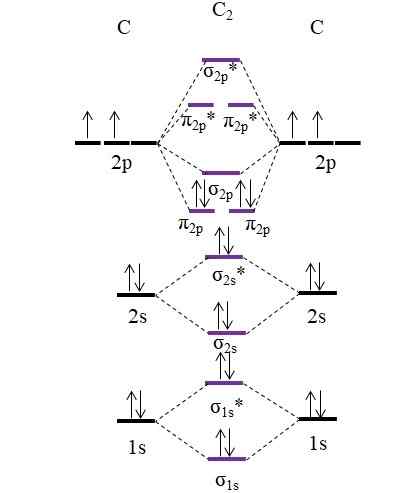OM -diagram for molekyl C2. Kilde: Gabriel Bolívar.

Nå er de to nye elektronene levert av karbonatomer plassert igjen i molekylære orbitaler π_{2 s} Men med motsatte spinn (Pauling Exclusion Principle).

Bestemme koblingsbestillingen vår vi vil ha:

enten.E = (8-4)/2

= 2

Merk at molekylære orbitaler π_{2 s} Legg til 4 elektroner binding til formelen. Å være denne ordren lik 2, betyr det at molekyl C₂ Den har en dobbeltbinding, c = c. Igjen, molekyl C₂, Også kalt diatomisk karbon, det er bare dampfase ved høye temperaturer, og det er en av de enkleste allotropiske former for karbon.

Og hva med C₂^2-? OM -diagrammet ditt er som følger:

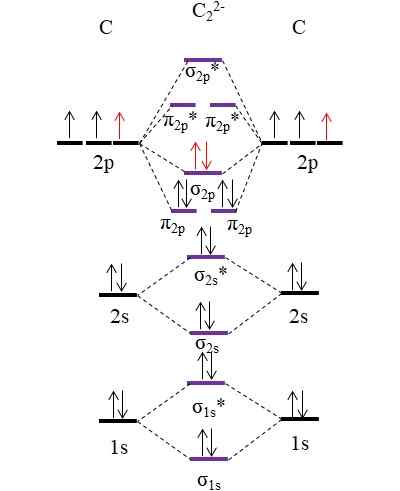Om diagram for anion C22-. Kilde: Gabriel Bolívar.

De to nye elektronene (røde piler) er plassert i den koblingsmolekylære orbitalen σ_{2 s}. Dette forutsetter således at hvert karbonatom bidrar med en av de to negative ladningene (for en oksidasjonstilstand på -1).

Kan tjene deg: kvikksølv fulminere: struktur, egenskaper, innhenting, bruk

Beregning av koblingsbestillingen vi vil ha:

enten.E = (10-4)/2

= 3

Det vil si anion c₂^2-, Også kalt Anion Acetyluro, den har en trippelkobling, [C≡C]^2-. Det er en relativt stabil anion med en stor koblingsstyrke; Avhengig av motstykkeioner kan det imidlertid stamme eksplosive forbindelser.

N₂ og n₂⁺

Det berømte nitrogenmolekylet, n₂, Det kan også beskrives perfekt ved å bruke molekylære orbitaldiagrammer:

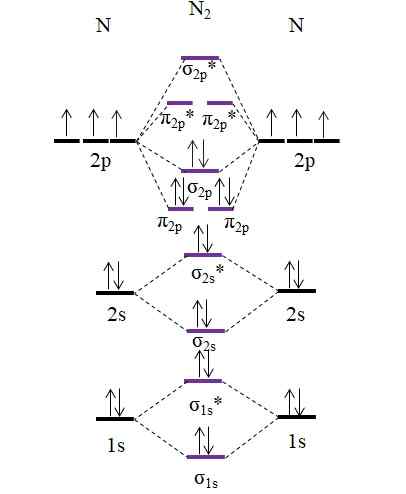OM -diagram for N2 -molekylet. Kilde: Gabriel Bolívar.

Merk at dette diagrammet er nøyaktig det samme som for anion C₂^2-. Dette betyr at n₂ og c₂^2- De er isolektroniske. Slikt faktum innebærer imidlertid ikke at begge artene oppfører seg på samme måte. Deretter₂, nøytral, er mye mer stabil enn C₂^2-, Negativ, selv om begge har en koblingsrekkefølge lik 3, N≡N.

Og hva med kation n₂⁺? La oss se på OM -diagrammet ditt:

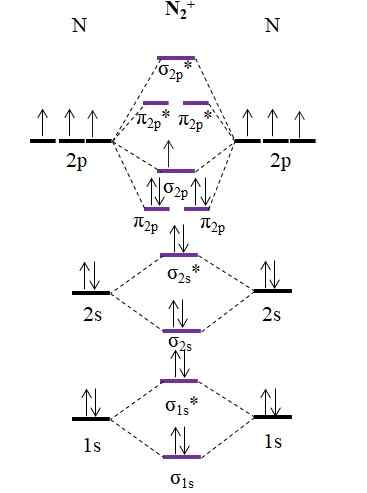Om diagram for kation n2+. Kilde: Gabriel Bolívar.

Som kation n₂⁺ Den har ett mindre elektron, dette fjernes molekylær orbital σ_{2 s}. Deretter₂ Det er diamagnetisk, mens n₂⁺ Det er paramagnetisk. Og hans koblingsordre er:

enten.E = (9-4)/2

= 2.5

En 2 2 -lenke.5 ville være representert med to linjer og ett punkt. Imidlertid gir ikke noe saken mye mening i Valencias teori eller i Lewis strukturer. Fordi denne koblingsordren er mindre enn 3, kraften til lenken som er til stede i n₂⁺ er lavere enn n₂, Så det er mer ustabilt.

ENTEN₂, ENTEN₂^2- Jeg₂²⁺

La oss nå se et annet veldig viktig molekyl for livet: molekylært eller diatomisk oksygen, eller₂. I følge Valencias teori og Lewis strukturer, skal den være diamagnetisk; Men eksperimentelt har det vist seg å være paramagnetisk, så det har forsvunnet elektroner et sted.

Nedenfor sammenligner vi OM -diagrammer for O₂ og ioner eller₂^2- (oksid) og o₂²⁺ (Oksidasjon):

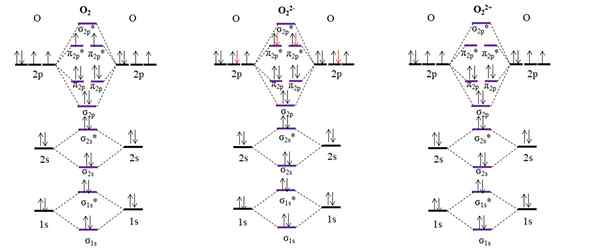OM -diagrammer for molekylært oksygen og to av hovedionene. Kilde: Gabriel Bolívar.

OM -diagrammet for o₂ Prøve, i motsetning til de forrige, at de molekylære orbitalene σ_{2 s} og π_{2 s} Endre energiposisjonen. Vi ser også effektivt at det er to manglende elektroner i orbitalene π_{2 s}*, som forklarer den paramagnetiske karakteren til oksygen (nevnt i begynnelsen av artikkelen).

På den annen side har vi også OM -diagrammet for anion eller₂^2-, uendelig spredt i kosmos (måner, planeter, kometer, asteroider osv.). Den har to ekstra elektroner (røde piler), som er ferdig med å fylle π -orbitalene_{2 s}*, parring av alle elektroner. Følgelig OR₂^2- Det er diamagnetisk.

Vi vurderer også OM -diagrammet for oksidasjon eller₂²⁺. Den har to elektroner mindre enn O₂, etterlater tomme orbitalene π_{2 s}*. Alle elektronene er sammenkoblet, og derfor er det diamagnetisk.

Lenke bestillinger for o₂, ENTEN₂^2- Jeg₂²⁺ De er henholdsvis: 2 (o = o), 1 [o-o]^2- og 3 [O≡O]²⁺. Derfor o₂²⁺ ville ha den sterkeste lenken.

Fordeler og ulemper

Fordeler

Blant fordelene med molekylær orbital teori kan vi sitere følgende:

-Det gjør det mulig å evaluere koblingsordrer som vanlig ikke ville gi mye mening i Valencia Link Theory

-Det korrelerer godt med diamagnetisme og paramagnetisme av molekyler

-Avstanden som skiller molekylære orbitaler i diagrammer er lik ΔE, og tjener til å forklare elektronisk overgangsprodukt av fotonabsorpsjon

-Gjelder ikke bare for homonukleære diatomiske molekyler, men også for heteronukleære molekyler, for eksempel CO₂ og benzen

-Den utvider modellen mot andre typer forbindelser, for eksempel uorganiske komplekser, så den støtter teorien om liganderfeltet

-Betraktet at elektroner flyttes gjennom molekylet er praktisk å forklare mange av de fysisk -kjemiske egenskapene

Ulemper

Og blant noen av ulempene med molekylær orbital teori har vi, for å avslutte:

-Det er veldig abstrakt og krever en dyp matematisk forståelse for å forstå den fullt ut

-Molekulasjonsdiagrammer som CO₂, Co, h₂Eller andre, de kan være for kjedelige til å utdype og forklare

-Han sier ingenting om spesifikke regioner eller lenker til et stort molekyl

-Det gir heller ingen informasjon angående molekylær geometri (trigonalt plan, firkantet plan, tetrahedral, etc.).

-Det er ikke så grafisk som Valencias koblingsteori

Den molekylære orbitalteorien er avslutning.

Referanser

1. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
2. Shiver & Atkins. (2008). Uorganisk kjemi. (Fjerde utgave). Mc Graw Hill.
3. Wikipedia. (2020). Orbital molekylær teori. Hentet fra: i.Wikipedia.org
4. Stephen Lower. (7. september 2020). Orbital molekylær teori. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org
5. Steven a. Hardinger. (2017). Orbital molekylær teori. Hentet fra: Chemed.Chem.Purdue.Edu
6. Pressbooks. (s.F.). Kapittel 8: Orbital molekylær teori. Hentet fra: OpenTextBc.Ac