Bolzano teorem

Vi forklarer hva Bolzanos teorem er, dens anvendelser og satte løse øvelser

Hva er Bolzanos teorem?

Han Bolzano teorem Den slår fast at hvis en funksjon er kontinuerlig på alle punkter i et lukket intervall [a, b] og det er oppfylt at bildet av “a” og “b” (under funksjonen) har motsatte tegn, så vil det være minst Ett punkt "C" i det åpne intervallet (A, B), slik at funksjonen evaluert i "C" vil være lik 0.

Dette teoremet ble uttalt av filosofen, teologen og matematikeren Bernard Bolzano i 1850. Denne forskeren, født i den nåværende Tsjekkia, var en av de første matematikken i historien som gjorde en formell demonstrasjon av egenskapene til kontinuerlige funksjon.

Forklaring av teorem

Bolzanos teorem er også kjent som teorem om mellomverdier, som hjelper til med å bestemme spesifikke verdier, spesielt nuller, av visse reelle funksjoner av en reell variabel.

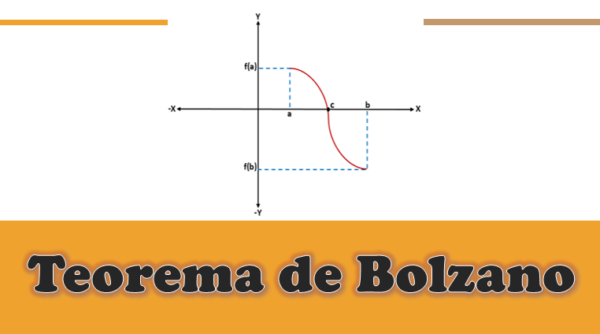
I en gitt funksjon fortsetter f (x) -det vil si at f (a) og f (b) er koblet sammen med en kurve-, hvor f (a) er under x -aksen (er negativ), og f (b) Med over x -aksen (det er positivt), eller omvendt, vil det være et skjærepunkt på X -aksen som vil representere en mellomverdi "C", som vil være mellom "A" og "B", og verdien av f (c) det vil være lik 0.

Når du grafisk analyserer Bolzanos teorem, kan det være kjent at for enhver kontinuerlig F -funksjon definert i et intervall [a, b], hvor f (a)_*f (b) er mindre enn 0, det vil være minst en rot "c" av den funksjonen innenfor intervallet (a, b).

Dette teoremet etablerer ikke antall punkter som eksisterer i det åpne intervallet, det sier bare at det er minst 1 poeng.

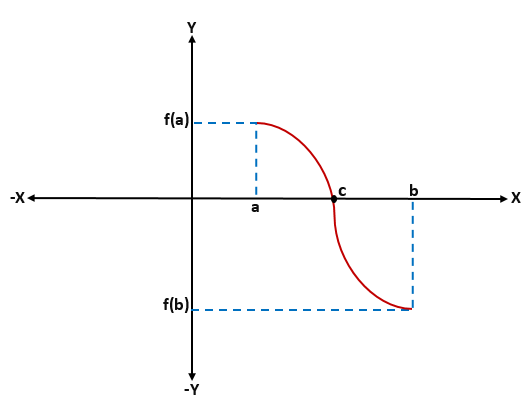
Demonstrasjon av Bolzano -teorem

For å demonstrere Bolzanos teorem antas det uten tap av generalitet at f (a) 0; På denne måten kan det være mange verdier mellom "A" og "B" som F (x) = 0, men det er bare nødvendig å demonstrere at det er en.

Kan tjene deg: imaginære tall: egenskaper, applikasjoner, eksempler

Det begynner å evaluere F ved midtpunktet (A+B)/2. Hvis f ((a+b)/2) = 0, slutter testen her; Ellers er f ((a+b)/2) positiv eller negativ.

En av halvdelene av intervallet [a, b] er valgt, slik at tegnene på funksjonen evaluert i endene er forskjellige. Dette nye intervallet vil være [A1, B1].

Nå, hvis F evaluert midt på [A1, B1] ikke er null, utføres den samme operasjonen før; Det vil si at halvparten av dette intervallet som oppfyller tilstanden til skiltene er valgt. Vær dette nye intervallet [A2, B2].

Hvis denne prosessen fortsetter, vil det være to suksesser an og Bn, slik at:

an vokser og Bn synker:

A ≤ a1 ≤ a2 ≤ ... ≤ en ≤ .. . ≤ .. . ≤ Bn ≤ .. . ≤ B2 ≤ B1 ≤ B.

Hvis lengden på hvert intervall [AI, BI] beregnes, må du:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Derfor er grensen når N har en tendens til uendelig (BN-AN) lik 0.

Å bruke den an vokser og begrenset og Bn er synkende og begrenset, det er en verdi "C" slik at:

A ≤ a1 ≤ a2 ≤ ... ≤ en ≤ .. .≤ C ≤ .. . ≤ Bn ≤ .. . ≤ B2 ≤ B1 ≤ B.

LIM -grensen er "C" og grensen for Bn er også "C". Derfor, gitt noen Δ> 0, er det alltid en "n" slik at intervallet [An, Bn] er inneholdt i intervallet (C-Δ, C+Δ).

Nå må det vises at f (c) = 0.

Hvis f (c)> 0, er det en slik f. Som nevnt ovenfor er det imidlertid en "n" verdi slik at f endrer logg på [an, bn] og i tillegg [an, bn] er inneholdt i (c -ε, c+ε), hva som er en motsetning.

Hvis f (c) 0 slik at f er negativ gjennom hele intervallet (c -ε, c+ε); Men det er en "n" -verdi som F endrer logg på [an, Bn]. Det viser seg at [an, Bn] er inneholdt i (C -ε, C+ε), som også er en motsetning.

Kan tjene deg: tegn på gruppering

Derfor f (c) = 0, og det er dette som ønsket å bli demonstrert.

Hva er Bolzano -teoremet for?

Fra sin grafiske tolkning brukes Bolzanos teorem for å finne røtter eller nuller i en kontinuerlig funksjon, gjennom bisensjon (tilnærming), som er en inkrementell søkemetode som alltid deler intervallene i 2.

Så hvis funksjonen endrer tegn på et intervall, blir F -funksjonen evaluert på midtpunktet, som uttrykkes som følger: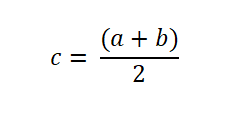Roten finnes når f (c) = 0. Hvis ikke, blir tegnet på F (c) analysert for å avgjøre om det er imot tegnet på f (a) eller det til f (b).

Deretter tas et intervall [a, c] eller [c, b] der endringen av skilt oppstår, og prosessen gjentas til intervallet er mindre og mindre, for å nærme seg verdien du ønsker; det vil si til verdien som funksjonen gjør 0.

Oppsummert, for å anvende Bolzano -teoremet og dermed finne røttene, begrense nulene til en funksjon eller gi en løsning på en ligning, utføres følgende trinn:

1. Det er bekreftet hvis F er en kontinuerlig funksjon i intervallet [a, b].
2. Hvis intervallet ikke er gitt, må man finne en der funksjonen er kontinuerlig.
3. Det er bekreftet hvis endene av intervallet gir motsatte tegn når de blir evaluert i F.
4. Hvis det ikke oppnås motsatte tegn, må intervallet deles inn i to underintervaller ved bruk av midtpunktet.
5. Evaluer funksjonen på midtpunktet og bekreft at Bolzano -hypotesen er oppfylt, der f (a) _* f (b) < 0.
6. Avhengig av tegnet (positivt eller negativt) av verdien som er funnet, gjentas prosessen med en ny underintervall til den nevnte hypotesen er oppfylt.

Kan tjene deg: Ikke -lineær programmering: Metoder og øvelser

Løste øvelser

Oppgave 1

Bestem om funksjonen f (x) = x² - 2, har minst en reell løsning i intervallet [1,2].

Løsning

Du har funksjonen f (x) = x² - 2. Som det er polynom, betyr det at det er kontinuerlig i ethvert intervall.

Det blir bedt om å avgjøre om den har en reell løsning i intervallet [1, 2], så nå trenger du bare å erstatte endene av intervallet i funksjonen for å vite tegnet på disse og vite om de oppfyller tilstanden til å være annerledes:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negativ)

f (2) = 2² - 2 = 2 (positivt)

Derfor tegn på f (1) ≠ tegn f (2).

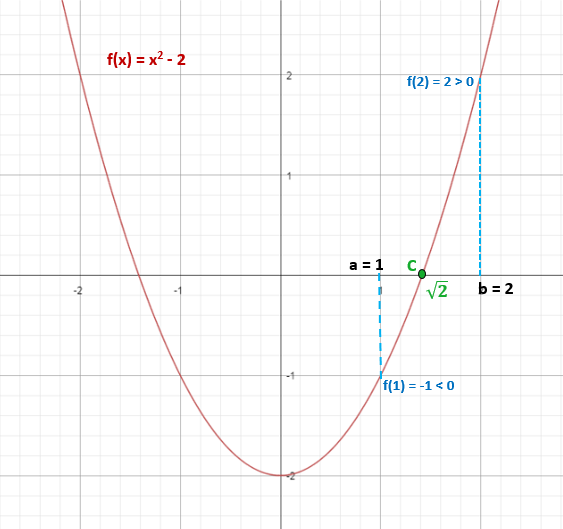
Dette sikrer at det er minst ett punkt "C" som tilhører intervallet [1,2], der f (c) = 0.

I dette tilfellet kan "C" -verdien beregnes enkelt som følger:

x² - 2 = 0

x = ± √2.

Dermed tilhører √2 ≈ 1,4 intervallet [1,2] og oppfyller at f (√2) = 0.

Oppgave 2

Demonstrere at ligning x⁵ + x + 1 = 0 har minst en reell løsning.

Løsning

Først bemerker vi at f (x) = x⁵ + X + 1 er en polynomfunksjon, noe som betyr at den er kontinuerlig i alle reelle tall.

I dette tilfellet er det ikke gitt noen intervall, så du må velge verdier intuitivt, helst nær 0, for å evaluere funksjonen og finne endringene av tegn:

Hvis intervallet [0, 1] brukes, må det:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Ettersom det ikke er noen tegnendring, gjentas prosessen med et annet intervall.

Hvis intervallet [-1, 0] brukes, må du:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

I dette intervallet er det en tegnendring: tegn på F (-1) ≠ tegn på F (0), noe som betyr at funksjonen F (x) = x⁵ + X + 1 har minst en ekte rot “c” i intervallet [-1, 0], slik at f (c) = 0. Med andre ord, det er sant at x⁵ + x + 1 = 0 har en reell løsning i intervallet [-1,0].