Lamys teorem
- 4799
- 1188
- Jonathan Carlsen

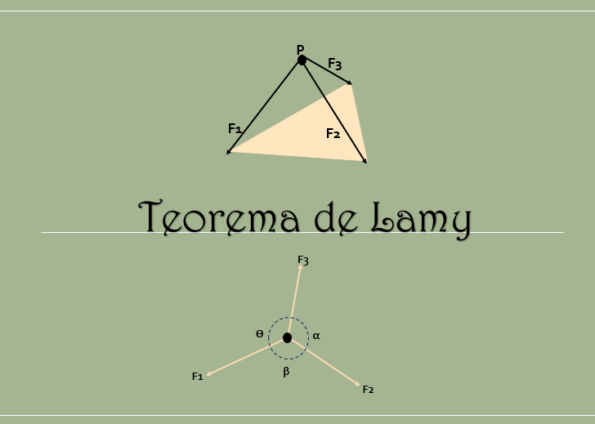
Lamys teorem slår fast at når et stivt legeme er i balanse og på handlingen fra tre koblingskrefter (krefter som er i samme plan), stemmer deres handlingslinjer på samme punkt.
Teoremet ble trukket av den franske fysikeren og religiøse. Det er mye brukt for å finne verdien av en vinkel, handlingslinjen til en kraft eller for å danne styrkenes trekant.
Forklaring
Teoremet slår fast at for at balansen skal oppfylles, må styrkene være koplaner; det vil si at summen av kreftene som utøves på et punkt er null.
I tillegg, som det fremgår av følgende bilde, blir det oppfylt at ved å forlenge handlingslinjene til disse tre styrkene, er de enig på samme punkt.
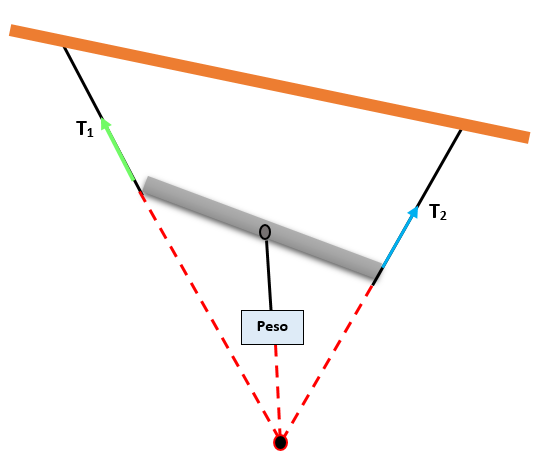
Således, hvis tre krefter som er i samme plan og samtidig, vil størrelsen på hver kraft være proporsjonal med brystet i motsatt vinkel, som dannes av de to andre kreftene.
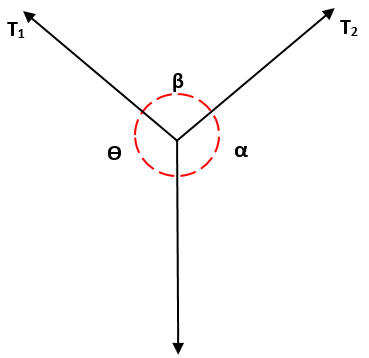
Dette må T1, med start fra brystet til α, er lik forholdet mellom T2 / β, som igjen er lik forholdet mellom T3 / ɵ, det vil si:
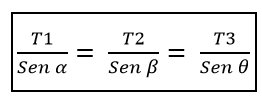
Derfra følger det at modulene til disse tre kreftene må være de samme hvis vinklene som danner hvert styrspar er lik 120º.
Det er muligheten for at et av vinklene er stump (mål mellom 900 og 1800). I så fall vil brystet i den vinkelen være lik brystet i tilleggsvinkelen (i paret måler det 1800).
Kan tjene deg: EksponentloverTrening løst
Det er et system dannet av to J- og K -blokker, som henger på flere strenger som danner vinkler med hensyn til horisontalt, som vist på figuren. Systemet er i likevekt og J -blokken veier 240 N. Bestem vekten av blokk K.
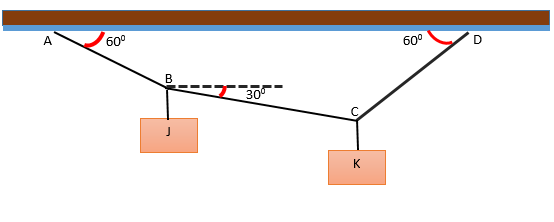
Løsning
Ved handlingsprinsippet og reaksjonen vil spenningene som utøves i blokk 1 og 2 være lik vekten av disse.
Nå er et gratis kroppsdiagram bygget for hver blokk og bestemmer dermed vinklene som danner systemet.
Det er kjent at tauet som går til A til B, har en vinkel på 300 , slik at vinkelen som kompletterer den er lik 600 . På den måten når du 900.
På den annen side, der punkt A ligger, er det en vinkel på 600 med hensyn til det horisontale; Vinkelen mellom vertikal og tTIL Det vil være = 1800 - 600 - 900 = 300.
Dermed oppnås det at vinkelen mellom AB og BC = (300 + 900 + 300) og (600 + 900 + 60) = 1500 og 2100. Når du blir med, bekreftes det at den totale vinkelen er 3600.
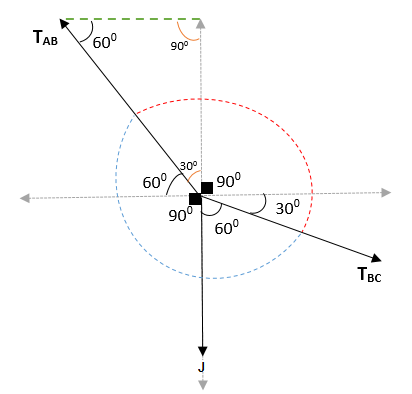
Bruker Lamys teorem du må:
TBC/ sin 1500 = STIL/ sin 1500
TBC = STIL
TBC = 240n.
På punkt C, hvor er blokken, er vinkelen mellom det horisontale og BC -tauet 30 er 300, Så den komplementære vinkelen er lik 600.
På den annen side er det en vinkel på 600 på CD -punktet; Vinkelen mellom vertikal og tC Det vil være = 1800 - 900 - 600 = 300.
Kan tjene deg: Coplanares Points: Ligning, eksempel og løste øvelserDermed oppnås det at vinkelen i blokk K er = (300 + 600)
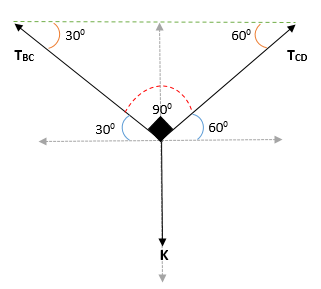
Bruke Lamys teorem på punkt C:
TBC/ sin 1500 = B / sin 900
Q = tBC * Sen 900 / sin 1500
Q = 240 n * 1/0,5
Q = 480 N.
Referanser
- Ferdinand p. Øl, e. R. (2013). Mekanikk for ingeniører, statisk. McGraw-Hill Inter-American.
- Francisco Español, J. C. (2015). Løst lineære algebraproblemer. Paraninfo Editions, S.TIL.
- Graham, J. (2005). Styrke og bevegelse. Houchton Mifflin Harcourt.
- Harpe, p. d. (2000). Temaer i geometrisk gruppeteori. University of Chicago Press.
- P. En tpler y, g. M. (2005). Fysikk for vitenskap og teknologi. Volum I. Barcelona: Gå tilbake.TIL.

