Norton Teorem Beskrivelse, applikasjoner, eksempler og øvelser

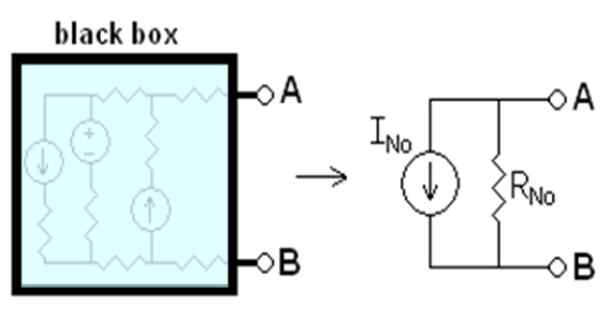
Han Norton Teorem, som gjelder elektriske kretsløp, fastslår at en lineær krets med to terminaler A og B, kan erstattes av en annen helt ekvivalent, bestående av en strømkilde som heter I_Nei koblet parallelt med en motstand r_Nei.

Sa nåværende i_Nei jeg hørte_N Det er den som ville flyte mellom punkt A og B, hvis de var kortsluttet. Motstanden r_N Det er den tilsvarende motstanden mellom terminalene, når alle uavhengige kilder er deaktivert. Alt som er sagt er skjematisert i figur 1.

Figur 1. Nortons tilsvarende krets. Kilde: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Den svarte boksen i figuren inneholder den lineære kretsen som vil bli erstattet av dens Norton -ekvivalent. En lineær krets er en der inngangen og utgangen har en lineær avhengighet, for eksempel forholdet mellom spenning V og likestrømmen I i et ohmisk element: V = I.R.

Dette uttrykket tilsvarer Ohms lov, der R er motstand, noe som også kan være en impedans, hvis det er en vekselstrømskrets.

Nortons teorem ble utviklet av elektriker og oppfinner Edward L Engineer. Norton (1898-1983), som jobbet lenge for Bell Laboratories.

[TOC]

Norton Teorem -applikasjoner

Når de har veldig kompliserte nettverk, med mange motstand eller impedanser og du vil ha en mindre og mer håndterbar krets.

På denne måten er Nortons teorem veldig viktig når du designer kretsløp med flere elementer, samt å studere deres respons.

Forholdet mellom Norton og Thevenins teoremer

Nortons teorem er det doble Thevenins teorem, noe som betyr at de er likeverdige. Thevenins teorem indikerer at den svarte boksen i figur 1 kan erstattes av en seriespenningskilde med en motstand, kalt thevenin r motstand_Th. Dette kommer til uttrykk i følgende figur:

Kan tjene deg: Materialmekanikk: Historie, studieretning, applikasjoner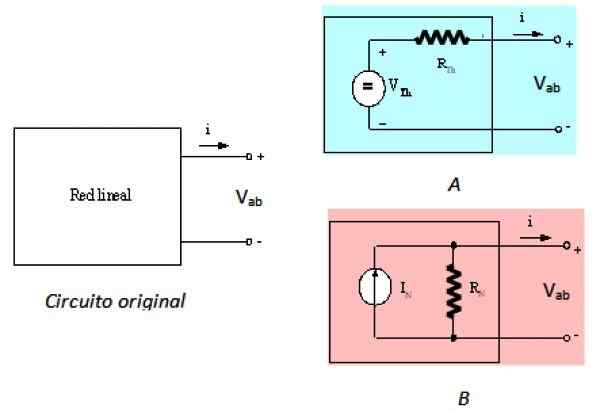 Figur 2. Original venstre krets, og ekvivalenter fra Thévenin og Norton. Kilde: f. Zapata.

Venstre krets er den originale kretsen, det lineære nettverket i den svarte boksen, kretsen opp til høyre er tilsvarer thevenin og kretsen B Det er Nortons tilsvarende, som beskrevet. Sett fra terminalene A og B, er de tre kretsene likeverdige.

Observer nå det:

-I den opprinnelige kretsen er spenningen mellom terminalene V_AB.

-V_AB  = V_Th i kretsen TIL

-Til slutt, v_AB  = Jeg_N.R_N i kretsen B

Hvis terminalene A og B er kortslutning i de tre kretsene, må det oppfylles at spenningen og strømmen mellom disse punktene må være den samme for de tre, siden de er likeverdige. Så:

-I den opprinnelige kretsen er strømmen jeg.

-For krets a er strømmen i = v_Th / R_Th, I henhold til Ohms lov.

-Endelig i krets B er strømmen jeg_N

Derfor konkluderes det med at motstandene til Norton og Thevenin har samme verdi, og at strømmen er gitt av:

i = i_N = V_Th / R_Th = V_Th / R_N

Eksempel

For å bruke Nortons teorem riktig, følges følgende trinn:

-Kretsdelen som Norton -ekvivalenten vil bli funnet fra nettverket er isolert fra nettverket.

-I den gjenværende kretsen, indikerer terminalene A og B.

-Bytt ut spenningskildene med kortslutning og strøm med åpne kretsløp, for å finne den tilsvarende motstanden mellom terminalene A og B. Dette er r_N.

-Returner alle kilder til sine opprinnelige posisjoner, kortslutter terminalene A og B og finn strømmen som sirkulerer mellom dem. Dette er jeg_N.

Kan tjene deg: Doppler Effekt: Beskrivelse, Formler, tilfeller, eksempler

-Tegn Norton -ekvivalentkretsen i henhold til det som er indikert i figur 1. Både nåværende kilde og tilsvarende motstand er parallelt.

Du kan også bruke Thevenins teorem for å finne r_Th, som vi allerede vet er lik R_N, Så etter Ohms lov kan du finne jeg_N Og den resulterende kretsen trekkes.

Og nå la oss se på et eksempel:

Finn Nortons ekvivalent mellom punkt A og B i følgende krets:

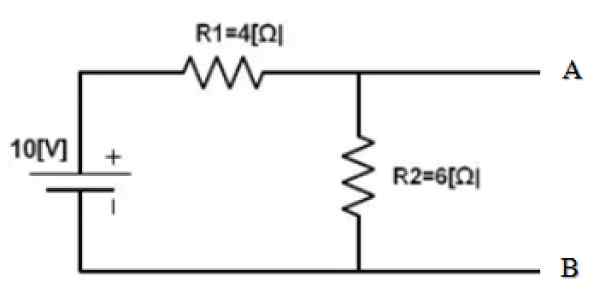Figur 3. Eksempelkrets. Kilde: f. Zapata.

Den delen av kretsen er allerede isolert hvis ekvivalent må finnes. Og punkt A og B er tydelig bestemt. Det som følger er å kortslutte 10 V -kilden og finne den tilsvarende motstanden til kretsen oppnådd:

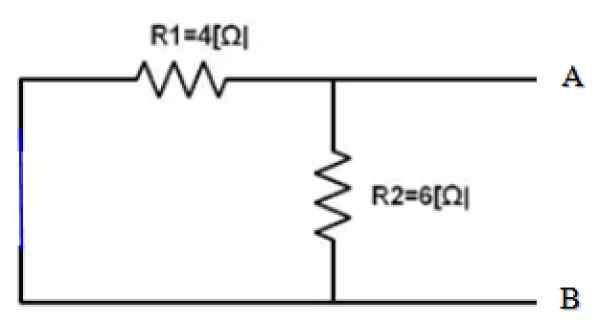Figur 4. Kortkrets kilde. Kilde: f. Zapata.

Visninger fra terminalene A og B, begge motstander r₁ og r₂ De er derfor parallelle:

1/r_Eq = 1/r₁₂ = (1/4) + (1/6) ω^-1 = 5/12 Ω^-1  → R_Eq = 12/5 Ω = 2.4 Ω

Deretter returneres kilden til sin plass og punktene A og B er kortslutning for å finne strømmen som sirkulerer der, dette vil være_N. I så fall:

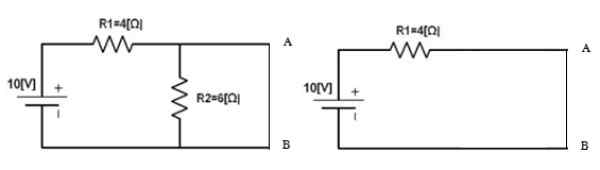Figur 5. Krets for å beregne Norton -strømmen. Kilde: f. Zapata.

Yo_N = 10 V / 4 Ω = 2.5 a

Norton -ekvivalent

Til slutt er Nortons ekvivalent med verdiene som er funnet, tegnet:

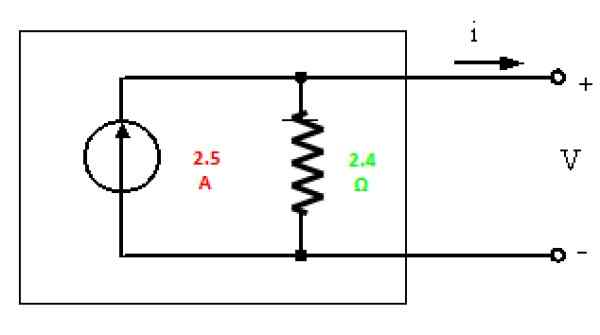Figur 6. Norton -ekvivalent av kretsen i figur 3. Kilde: f. Zapata.

Trening løst

I kretsen til følgende figur:

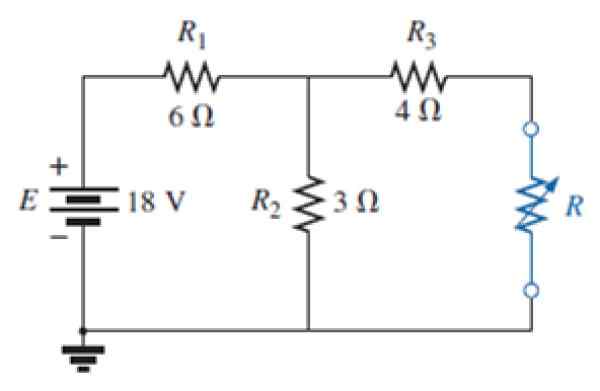Figur 7. Krets for øvelsen løst. Kilde: Alexander, C. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.

a) Finn Nortons tilsvarende krets for det ytre blå motstandsnettverket.

b) Finn også Thévenins ekvivalent.

Løsning på

Etter trinnene som er angitt ovenfor, må kilden være kortslutning:

Kan tjene deg: Diffraksjon av lyd: Hva består av eksempler, applikasjoner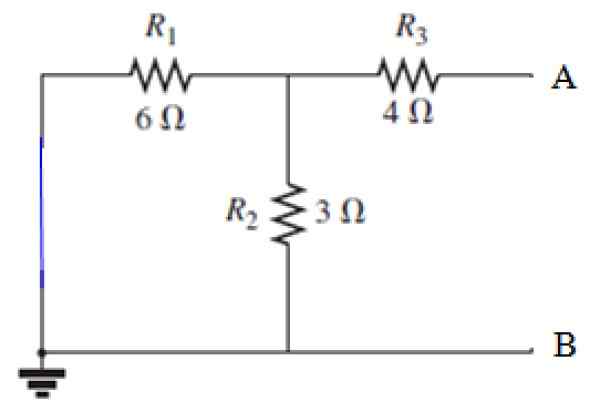 Figur 8. Kort kretsskilde i kretsen i figur 7. Kilde: f. Zapata.

RN -beregning

Utsikt fra terminalene A og B, motstand R₃ er i serie med parallellen dannet av motstandene r₁ og r₂, La oss først beregne den tilsvarende motstanden til denne parallellen:

1/r₁₂ = (1/6)+ (1/3) Ω^-1 = 1/2 Ω^-1  → R_Eq = 2/1 Ω = 2Ω

Og så er denne parallellen i serie med r_3, slik at den tilsvarende motstanden er:

R_Eq = 2 Ω + 4 Ω = 6 Ω

Dette er verdien av begge r_N som av r_Th, Som forklart før.

Beregning av i

Deretter er terminalene A og B kortslutning, og returnerer kilden til sin plass:

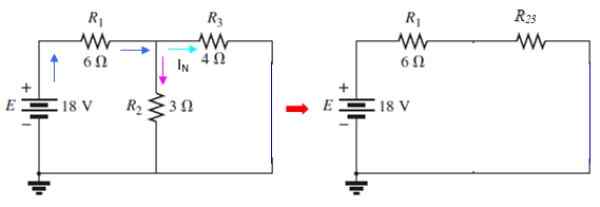Figur 9. Norton strømkretser. Kilde: f. Zapata.

Strømmen som går gjennom i₃ er den nåværende jeg_N søkt, som kan bestemmes med nettmetoden eller ved bruk av serier og parallell. I denne kretsen r₂ og r₃ De er parallelle:

1/r₂₃ = (1/3)+ (1/4) Ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Motstanden r₁ Det er i serie med denne parallellen, da:

R₁₂₃ = 6 + (12/7) ω = 54/7 Ω

Strømmen som kommer ut av kilden (blå farge) beregnes etter Ohms lov:

V = i. R → i = v/r = 18 V/(54/7 Ω) = 7/3 a

Denne strømmen er delt inn i to deler: en som krysser r₂ Og en annen som krysser r₃. Imidlertid strømmen som krysser parallellen R₂₃ Det er det samme som går gjennom r₁, Som det kan sees i figurens mellomkrets. Spenningen der er:

V₂₃ = Jeg.R₂₃ = (7/3) a .(12/7) ω = 4 V

Begge motstandene r₂ og r₃ De er på den spenningen, siden de er parallelle, derfor:

Yo₃ = V₂₃ / R₃ = 4 v / 4 Ω = 1 a

Vi har allerede søkt Norton -strømmen, siden jeg tidligere sagt jeg₃ = Jeg_N, så:

Yo_N = 1 a

Norton -ekvivalent

Alt er klart til å tegne Norton -ekvivalenten til denne kretsen mellom punkt A og B:

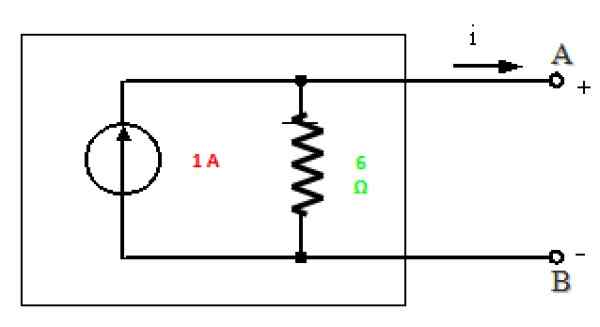Figur 10. Norton -ekvivalent av kretsen i figur 7. Kilde: f. Zapata.

Løsning b

Å finne Thévenins ekvivalent er veldig enkelt, siden r_Th = R_N= 6 Ω og som forklart i de foregående seksjonene:

V_Th = Jeg_N. R_N = 1 a . 6 Ω = 6 V

Thévenins tilsvarende krets er:

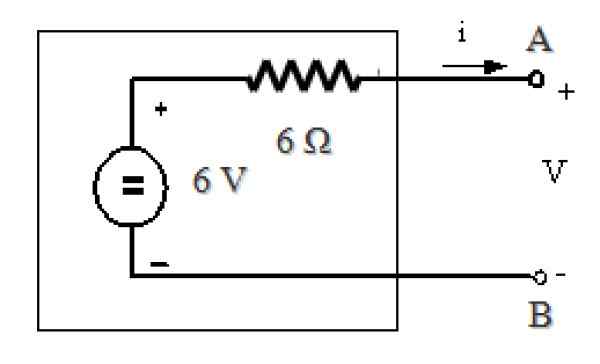Figur 11. Thevenins ekvivalent med kretsen i figur 7. Kilde: f. Zapata.

Referanser

1. Alexander, ca. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.
2. Boylestad, r. 2011. Introduksjon til kretsanalyse. 2. Utgave. Pearson.
3. Dorf, r. 2006. Introduksjon til elektriske sirkud. 7. Utgave. John Wiley & Sons.
4. Edminister, J. nitten nittiseks. Elektriske kretsløp. Schaum -serien. 3. Utgave. Mc Graw Hill.
5. Wikipedia. Norton Teorem . Gjenopprettet fra: det er.Wikipedia.org.