Overleggs teorem Forklaring, applikasjoner, øvelser løst

Han Superposisjonsteorem, I elektriske kretsløp slår det fast at spenningen mellom to punkter, eller strømmen gjennom dem, er den algebraiske summen av spenningen (eller av strømningene hvis det er tilfelle), på grunn av hver kilde, som om hver og en virker i en måte uavhengig.

Dette teoremet tillater analyse av lineære kretsløp som inneholder mer enn en uavhengig kilde, siden det bare er nødvendig å beregne bidraget til hver separat.

Lineær avhengighet er avgjørende for teoremet å bruke. En lineær krets er at hvis respons er direkte proporsjonal med oppføringen.

For eksempel fastslår Ohms lov som ble brukt på en elektrisk motstand V = i.R, hvor V Det er spenningen, R er motstanden og Yo Det er strømmen. Det er da en lineær avhengighet av spenning og strøm i en motstand.

I lineære kretsløp brukes superposisjonsprinsippet under hensyntagen til følgende:

-Hver uavhengig spenningskilde må vurderes separat, og for dette er det nødvendig å slå av alle de andre. Det er nok å sette til 0 v alle de som ikke er under analyse eller erstatte dem i ordningen med en kortslutning.

-Hvis kilden er, må kretsen åpnes.

-Når den indre motstanden til både strøm- og spenningskilder vurderes, må disse forbli på plass, og være en del av resten av kretsen.

-Hvis det er avhengige kilder, må de være som det vises i kretsen.

[TOC]

applikasjoner

Overlappende teorem brukes til å oppnå enklere og enklere kretsløp å håndtere. Men det må huskes som bare gjelder de med lineære svar, som det fremgår av i begynnelsen.

Da kan den ikke brukes direkte til å beregne kraften for eksempel, siden strømmen er relatert til strømmen gjennom:

P = i² R

Siden strømmen er kvadrat, er ikke svaret lineært. Det er heller ikke aktuelt for magnetiske kretsløp der transformatorer griper inn.

Kan tjene deg: dynamisk elektrisitet

På den annen side gir superposisjonsteorem muligheten til å vite effekten hver kilde på kretsen har. Og selvfølgelig, gjennom anvendelsen er det mulig å løse det fullstendig, det vil si å kjenne strømmer og spenninger gjennom hver motstand.

Overlappsteoremet kan også brukes i forbindelse med andre kretsteoremer, for eksempel for thévenin, for å løse mer komplekse konfigurasjoner.

I vekslende strømkretser er teoremet også nyttig. I dette tilfellet jobber vi med impedanser i stedet for motstander, så lenge den totale responsen til hver frekvens av uavhengig kan beregnes.

Til slutt, i elektroniske systemer, er teoremet aktuelt for både direkte og alternativ gjeldende analyse, separat.

Trinn for å bruke overlappende teorem

-Deaktiver alle uavhengige kilder etter instruksjonene gitt i begynnelsen, bortsett fra den som skal analyseres.

-Bestem utgangen, enten spenning eller strøm, som produserer den enkeltkilden.

-Gjenta de to trinnene som er beskrevet for alle andre kilder.

-Beregn den algebraiske summen av alle bidragene som finnes i de foregående trinnene.

Løste øvelser

Eksemplene løst nedenfor avklarer bruken av teoremet i noen enkle kretsløp.

- Eksempel 1

I kretsen vist i følgende figur, finn strømmen som krysser hver motstand gjennom overlappingsteoremet.

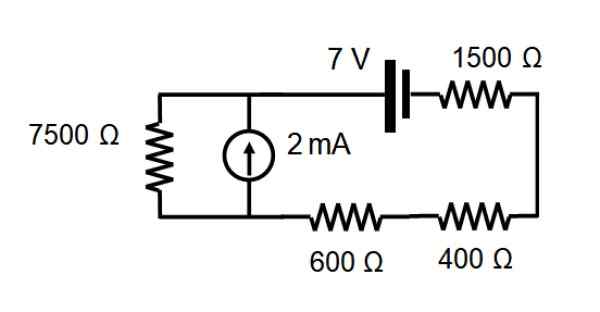
Løsning

Spenningskildebidrag

For å starte den nåværende kilden elimineres det, som kretsen forblir på denne måten:

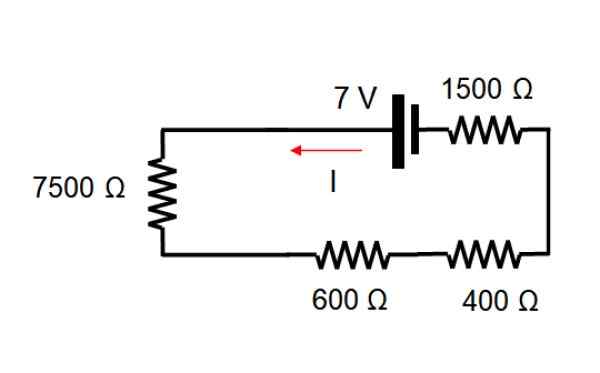
Den tilsvarende motstanden tilfører verdien av hver motstand, siden de alle er i serie:

7500 +600 +400 +1500 Ω = 10.000 Ω

Bruke Ohms lov V = i.R Og rydde strømmen:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 ma

Denne strømmen er den samme for all motstand.

Kan tjene deg: Millikan Eksperiment: Prosedyre, forklaring, betydning

Bidrag fra den nåværende kilden

Spenningskilden elimineres umiddelbart, for å fungere bare med gjeldende kilde. Den resulterende kretsen er vist nedenfor:

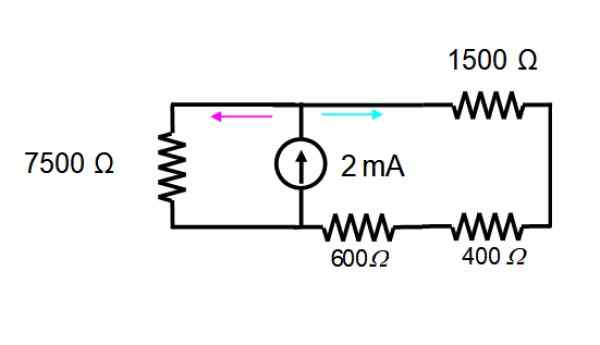
Motstandene i nettet til høyre er i serie og kan erstattes av bare en:

600 +400 + 1500 Ω = 2500 Ω

Den resulterende kretsen er slik:

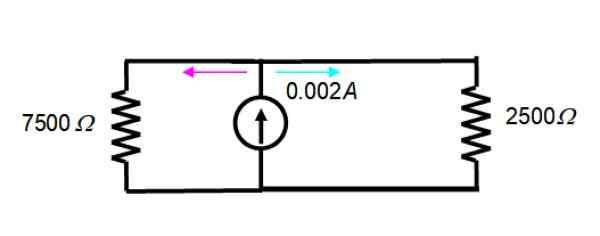
Strømmen på 2 mA = 0.002 a er delt mellom de to motstandene til figuren, derfor er ligningen for den nåværende divisoren gyldig:

Yo_x = (R_Eq/R_x) Yo_T

Hvor Yo_x er strømmen i motstand R_x, R_Eq symboliserer tilsvarende motstand og Yo_T er den totale strømmen. Det er nødvendig å finne den tilsvarende motstanden mellom dem, vel vitende om at:

1/r_Eq = (1/ r₁) + (1/ r₂)

Derfor:

1/r_Eq = (1/7500) + (1/2500) = 1/1875 → R_Eq = 1875 Ω

For denne andre kretsen erstatter strømmen som passerer gjennom motstanden til 7500 Ω verdier i den nåværende delingslikningen:

Yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 a = 0.5 ma

Mens den som går gjennom 2500 Ω motstanden er:

Yo_{2500 Ω} = 2 ma - 0.5 ma = 1.5 ma

Superposisjonsteorem -søknad

Nå brukes overlappingsteoremet for hver motstand, og starter med 400 Ω:

Yo_{400 Ω} = 1.5 ma - 0.7 mA = 0.8 ma

Viktig: For denne motstanden trekkes strømningene, når de sirkulerer i motsatt retning, som det fremgår av den nøye observasjonen av figurene, der sansene til strømningene har forskjellige farger.

Den samme strømmen gjelder like mye motstanden på 1500 Ω og 600 Ω, siden de alle er i serie.

Deretter blir teoremet brukt for å finne strømmen gjennom motstanden til 7500 Ω:

Yo_{7500 Ω} = 0.7 Ma + 0.5 ma = 1.2 ma

Viktig: Når det. Igjen er det nødvendig å observere nøye sansene til strømningene.

Kan tjene deg: Relativ feil: Formler, hvordan det beregnes, øvelser

- Oppgave 2

Finn strømmen og spenningen gjennom motstanden til 12 Ω gjennom overlappende teorem.

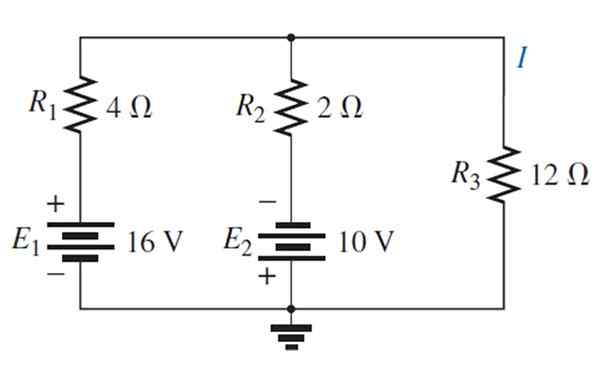
Løsning

Kilde E erstattes₁ Med en kortslutning:

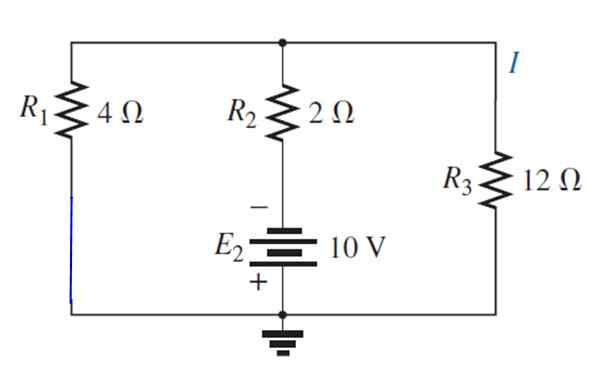
Den resulterende kretsen trekkes som følger, for enkelt å visualisere motstandene som forblir parallelt:

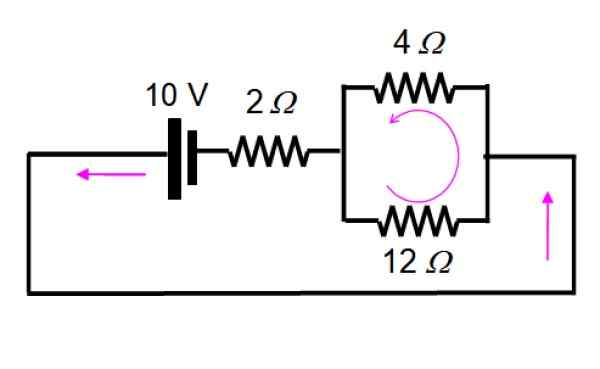
Og nå løses det ved å bruke serier og parallelle:

1/r_Eq = (1/12) + (1/4) = 1/3 → R_Eq = 3 Ω

Denne motstanden er i sin tur i serie med den av 2 Ω, Derfor er den totale motstanden 5 Ω. Den totale strømmen er:

I = v / r = 10 v / 5 Ω = 2 a

Denne strømmen er delt som:

Yo_12Ω = (3/12) 2 a = 0.5 a

Derfor er spenningen:

V_12Ω = 0.5 A × 12 Ω = 6 V

Nå er kilden aktivert₁:

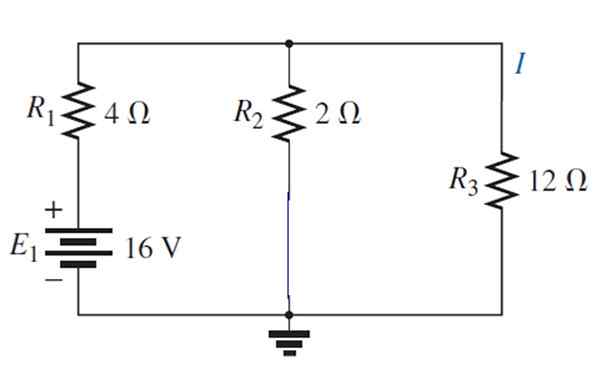
Den resulterende kretsen kan trekkes på denne måten:

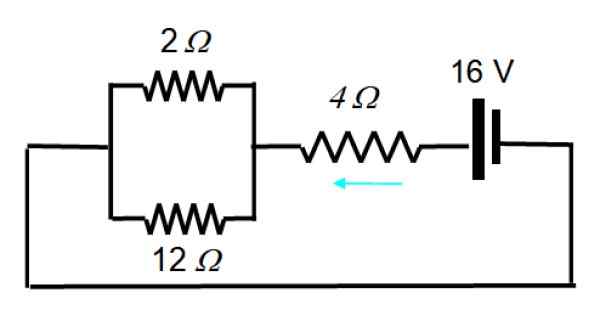
1/r_Eq = (1/12) + (1/2) = 7/12 → R_Eq = 12/7 Ω

Og i serie med 4 Ω Det er en tilsvarende motstand 40/7 Ω. I dette tilfellet er den totale strømmen:

I = v/r = 16 V/(40/7) Ω = 14/5 a

Spenningsdelingen med disse verdiene brukes igjen:

Yo_12Ω = ((12/7)/12) (14/5) A = 0.4 a

Den resulterende strømmen er: 0.femti.4 A = 0.1 a. Merk at de er trukket fra, fordi strømmen til hver kilde gir forskjellig betydning, som det kan sees i den opprinnelige kretsen.

Spenningen gjennom motstand er:

V_12Ω = 0.4 A × 12 Ω = 4.8 v

Endelig er den totale spenningen: 6 V-4.8 V = 1.2 v

Referanser

1. Alexander, ca. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.
2. Boylestad, r. 2011. Introduksjon til kretsanalyse. 2. Utgave. Pearson.
3. Dorf, r. 2006. Introduksjon til elektriske sirkud. 7. Utgave. John Wiley & Sons.
4. Edminister, J. nitten nittiseks. Elektriske kretsløp. Schaum -serien. 3. Utgave. Mc Graw Hill
5. Wikipedia. Nåværende divisor. Gjenopprettet fra: det er.Wikipedia.org.