Ortogonale matriseegenskaper, demonstrasjon, eksempler

Du har en Ortogonal matrise Når nevnte matrise multiplisert med transponering, resulterer det i identitetsmatrisen. Hvis det inverse av en matrise er lik den transponerte, er den opprinnelige matrisen ortogonal.

Ortogonale matriser er karakteristiske at antall rader er lik antall kolonner. I tillegg er radvektorer enhetens ortogonale vektorer og utslettet av transponerte vektorer er også.

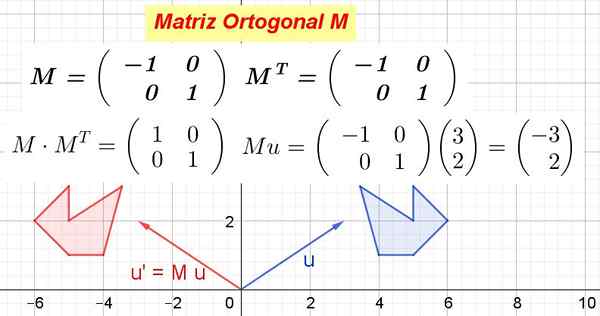Figur 1. Eksempel på ortogonal matrise og hvordan transformerer geometriske objekter. (Utarbeidet av Ricardo Pérez)

Når en ortogonal matrise multipliseres med vektorene til et vektorrom produserer en isometrisk transformasjon, det vil si en transformasjon som ikke endrer avstandene og bevarer vinklene.

En typisk representant for ortogonale matriser er Rotasjonsmatriser. Transformasjonene av ortogonale matriser på et vektorrom kalles Ortogonale transformasjoner.

De geometriske transformasjonene av rotasjon og refleksjon av punkter representert av dens kartesiske vektorer er laget ved å bruke ortogonale matriser på de originale vektorene for å oppnå koordinatene til de transformerte vektorene. Det er av denne grunn at ortogonale matriser er mye brukt i beregningsgrafisk prosessering.

[TOC]

Egenskaper

En matrise M Det er ortogonal hvis det multipliseres med transponering M^T Identitetsmatrisen resulterer i Yo. Tilsvarende produktet av transponering av en ortogonal matrise av den opprinnelige matrisen til identitetsmatrisen:

M m^T = M^T M = i

Som en konsekvens av den forrige uttalelsen, er den transponerte av en ortogonal matrise lik den omvendte matrisen:

M^T = M^-1.

Settet med ortogonale dimensjonsmatriser n x n De danner den ortogonale gruppen Eller (n). Og undergruppen av Eller (n) av ortogonale matriser med bestemmelse av +1 form Spesialmatriser Group ITS (N). Gruppens matriser Din (n) De er matriser som produserer lineære rotasjonstransformasjoner, også kjent som Rotasjonsgruppe.

Demonstrasjon

Vi vil demonstrere at en matris.

Kan tjene deg: Bayes teorem

Anta at rekkene til en ortogonal matrise n x n er n n ortonormale vektorer av dimensjon n. Hvis det er betegnet av v1, v2,.. ., vn N -vektorene er oppfylt:

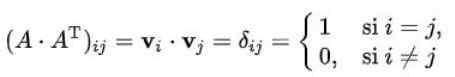
Der det er tydelig at settet med radvektorer er et sett med ortogonale vektorer med norm en.

Eksempler

Eksempel 1

Vis at 2 x 2 -matrisen som vektoren har i sin første rad V1= (-1 0) og i sin andre rad vektoren V2= (0 1) er en ortogonal matrise.

Løsning: Matrisen er bygget M og dens transponering beregnes M^T:

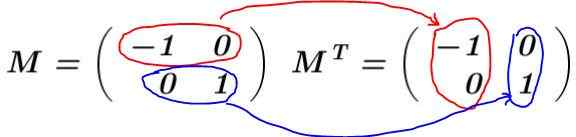
I dette eksemplet, matrisen M Det er en transponert bil, det vil si at matrisen og dens transponering er identisk. Det multipliserer M for sin transponering M^T:

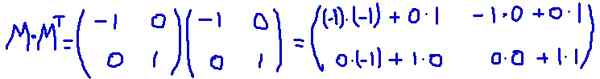
Det er bekreftet at M M^T Det er lik identitetsmatrisen:

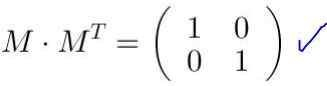
Når matrisen M Det multipliseres med koordinatene til en vektor eller et punkt, oppnås nye koordinater som tilsvarer transformasjonen som matrisen gjør på vektoren eller punktet.

Figur 1 viser hvordan M Transformerer vektoren eller i eller' Og også som M Transformere den blå polygonen til den røde polygonen. Som M Det er ortogonal, det er da en ortogonal transformasjon, som bevarer avstander og vinkler.

Eksempel 2

Anta at du har en 2 x 2 -matrise definert i reais gitt av følgende uttrykk:

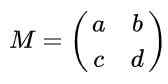
Finn de virkelige verdiene til til, b, c og d slik at matrisen M Være en ortogonal matrise.

Løsning: Per definisjon er en matrise ortogonal hvis multiplisert med transponering oppnås som et resultat av identitetsmatrisen. Å huske at den transponerte matrisen oppnås fra originalen, og utveksling av rader med kolonner er følgende likhet:

Det kan tjene deg: domene og motsetning av en funksjon (med eksempler)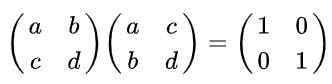

Utføre matrisemultiplikasjonen er:

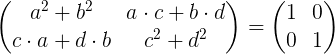
I likhet med elementene i venstre matrise med elementene i identitetsmatrisen til høyre, oppnår vi et system med fire ligninger med fire ukjente A, B, C og D.

Vi foreslår for A, B, C og D følgende uttrykk basert på trigonometriske grunner sinus og kosinus:

Med dette forslaget og på grunn av den grunnleggende trigonometriske identiteten, er den første og tredje ligningen i likheten mellom matrikselementene automatisk tilfredsstilt. Den tredje og fjerde ligningen er den samme og i matrise -likhet etter å ha erstattet de foreslåtte verdiene er slik:

som fører til følgende løsning:

Til slutt oppnås følgende løsninger for den ortogonale matrisen M:

Merk at den første av løsningene har en determinant +1, så den tilhører ITS -gruppen (2), mens den andre løsningen har en determinant -1 og derfor ikke tilhører denne gruppen.

Eksempel 3

Gitt følgende matrise, finn verdiene til A og B for å ha en ortogonal matrise.

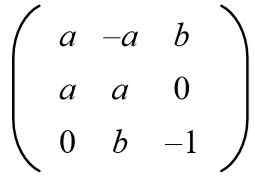
Løsning: For at en gitt matrise skal være ortogonal, må produktet med transponering være identitetsmatrisen. Deretter blir matriksproduktet fra matrisen gitt med sin transponerte matrise gjort og gir følgende resultat:

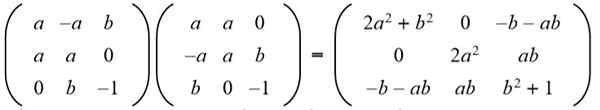
Deretter blir resultatet matchet med identitetsmatrisen 3 x 3:

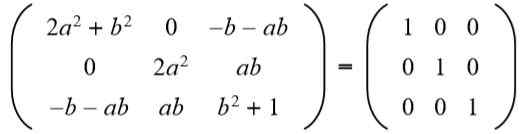
I andre rad tredje kolonne har du (A B = 0), men til Det kan ikke være null, for i så fall ville likheten mellom elementene i den andre raden og andre kolonne ikke bli oppfylt. Da nødvendigvis B = 0. Erstatte b For verdien 0 har vi:

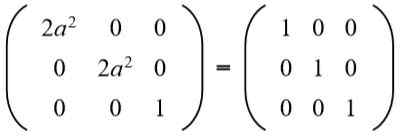
Da løses ligningen: 2a^2 = 1, hvis løsninger er: +½√2 og -½√2.

Kan tjene deg: typer vinkler, egenskaper og eksempler

Tar den positive løsningen til til Det resulterer i den følgende ortogonale matrisen:

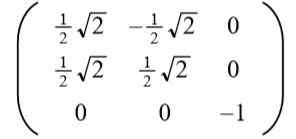
Leseren kan lett bekrefte at radvektorene (og også kolonnevektorer) er ortogonale og enhet, det vil si Ortonormal.

Eksempel 4

Demonstrere at matrisen TIL hvis rader er V1 = (0, -1 0), V2 = (1, 0, 0) og V3 = (0 0 -1) Det er en ortogonal matrise. Finn i tillegg hvordan vektorene til den kanoniske basen blir transformert I J k Til vektorene U1, U2 og U3.

Løsning: Det må huskes at elementet (i, j) av en matrise multiplisert med dens transponering, er skalarproduktet til vektoren til rad (i) med kolonnen (j) til transponering. I tillegg er dette produktet lik Kroneckers delta i tilfelle matrisen er ortogonal:

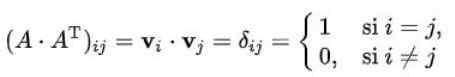
I vårt tilfelle er det slik:

V1 • V1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • V2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • V3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Med det som demonstreres at det er en ortogonal matrise.

I tillegg u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) og til slutt U3 = a k = (0, 0, -1)

Referanser

1. Anthony Nicolaides (1994) Determinanter og matriser. Passpublikasjon.
2. Birkhoff og Maclane. (1980). Moderne algebra, ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba m.  (2004) Introduksjon til lineær algebra. ESIC -redaksjon.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-sekunders matematikk: De 50 mest sinnsutvidende teoriene i matematikk. Ivy Press Limited.
7. Wikipedia. Ortogonal matrise. Gjenopprettet fra: er.Wikipedia.com
8. Wikipedia. Ortogonal matrise. Hentet fra: i.Wikipedia.com