Matte

Miletus slikt teorem

Miletus slikt teorem

Vi forklarer første og andre teorem av slikt, med eksempler og øvelser løst

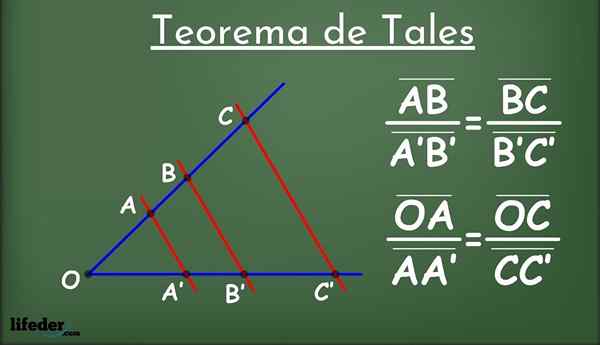
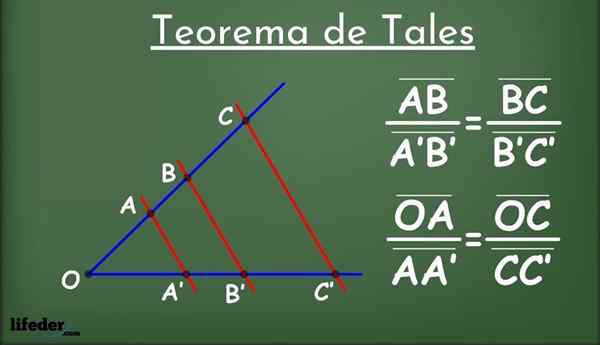Figur 1.- Tales Theorem

Hva er slikt?

Han Slikt teorem Fra Miletus refererer han faktisk til flere geometri -teoremer tilskrevet det gamle Hellas Thales of Miletus, som bodde fra 624 til 546 AC i Miletus, nåværende Tyrkia.

I tillegg til matematiker og geometer, var en slik filosof anerkjent for hans store skarphet. Det sies at han klarte å måle høyden på den store pyramiden gjennom bruk av en av dens teorier.

Han Første teorem om slikt Det refererer til segmentene som en gruppe parallelle linjer bestemmer i to linjer i flyet. Disse segmentene holder et forhold mellom proporsjonalitet, som det vil sees innen kort tid, som utvides til sidene av to trekanter, forutsatt at visse betingelser er oppfylt.

Dette teoremet er ekstremt nyttig i praksis, siden det tillater å bestemme høyden på veldig høy eller vanskelig tilgjengelig strukturer, uten å måtte måle dem direkte. Dette var nettopp hva historier gjorde da han målte høyden på den store pyramiden.

For sin del, Andre teorem om dette Koblingspunkter som tilhører en omkrets med et rektangel -trekant registrert i den, hvis hypotenuse sammenfaller med diameteren.

Første teorem om slikt

Være to linjer i et fly, kalt l1 og jeg2 (i blått i figur 1) og en gruppe linjer parallelt med hverandre (i rødt) som krysser l1 og jeg2.

Parallelle linjer deler linjene i segmentene l1 og jeg2: Ab, a'b ', bc, b'c' og så videre. Blant segmentene er det etablert følgende proporsjonalitetsforhold:

For eksempel beregnes i denne figuren av "X" -segmentet av teoremet til slikt, siden linjene er krysset av flere paralleller som bestemmer segmenter med kjent lengde:

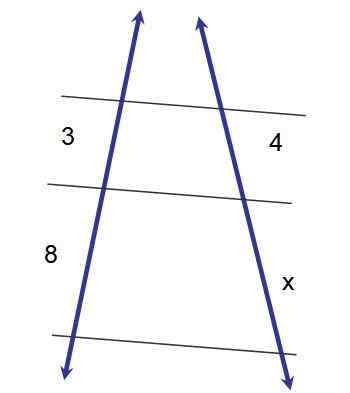Det kan tjene deg: gjensidig utelukkende hendelser: egenskaper og eksemplerFigur 2.- Anvendelse av den første slike teorem for å bestemme målet for segment x. Kilde: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Slikt teorem for lignende trekanter

Teoremet kan utvides til trekantene som følger: Anta at det er en ABC -trekant som et parallelt segment trekkes til en av sidene. På denne måten oppnås to lignende trekanter: ABC og DEC, hvis indre vinkler er kongruente, det vil si at de har like mål.

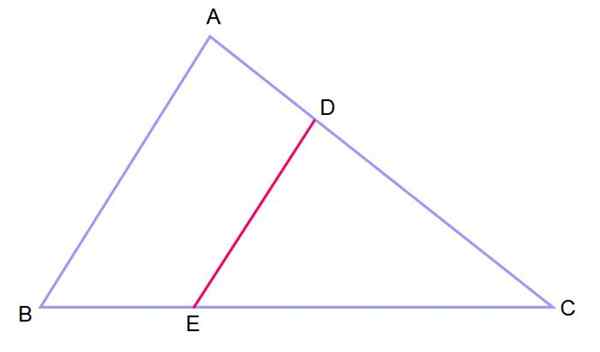Figur 3.- To trekanter i posisjonen til slike, med to parallelle sider og en felles vinkel, er like. Kilde: f. Zapata.

Når du har to trekanter ordnet på denne måten, sies det at de er i en slik posisjon.

Et forhold mellom proporsjonalitet mellom segmentene blir hevet på samme måte som for de parallelle linjene:

Som tilsvarer denne andre, mellom de tilsvarende sidene av hver trekant, også kalt homologe sider:

Hver av disse kvotientene kalles Likhetsgrunner. I lignende trekanter er årsaken til likhet lik kvotienten mellom omkretsene og kvadratet for likhetsforholdet er lik kvotienten mellom områdene.

Deretter et eksempel der slikt teorem kan brukes på lignende trekanter og finne ut hvor mye den ukjente siden x er verdt.

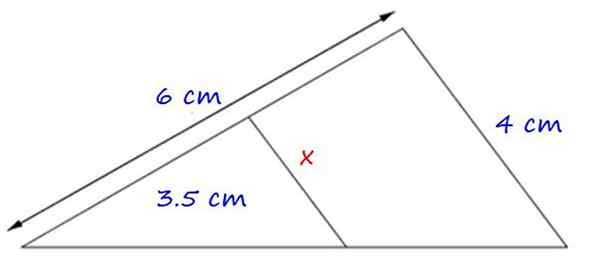Figur 4.- Søknadseksempel på det første slikt teorem. Kilde: f. Zapata.

Trekantene som er dannet er like, ettersom de har en felles vinkel og sidene X og 4 cm er parallelle.

Derfor er proporsjonaliteten mellom de tilsvarende sidene:

Og verdien av x blir lett fjernet:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Andre teorem om dette

Dette teoremet refererer til en trekant hvis toppunkter er punkter som tilhører en omkrets, noe som betyr at den er registrert i den.

I dette tilfellet slår teoremet fast at hver gang hypotenusa tilsvarer omkretsens diameter, er trekanten som således spores, rektangel, det vil si en av dens indre vinkler måler 90º, som sett i figur 5 til venstre.

Kan tjene deg: Symbolisering av uttrykk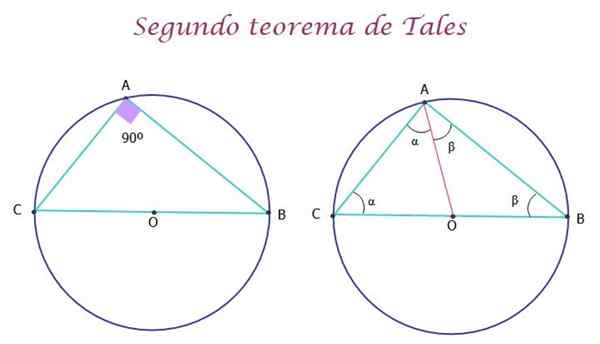Figur 5.- Den andre teoremet til slike sier at trekanten som er registrert i omkretsen er rektangel. Kilde: f. Zapata.

Demonstrasjon av den andre teoremet til slikt

Demonstrasjonen av teoremet er veldig enkel. I figuren over til høyre har AO -segmentet blitt trukket i rødt, for å danne de to AOC- og AOB -trekantene, som er isosceles, siden sidene OA, OC og OB er radioer i omkretsene og derfor måler de det samme.

På denne måten har trekantene to like vinkler, som er henholdsvis α og β. Nå, for den opprinnelige ABC -trekanten, som for enhver trekant, er det oppfylt at summen av tiltakene for dens indre vinkler er lik 180º, derfor:

α + (α + β) + β = 180º

Derfor:

2α + 2β = 180º

Derfor:

2 (α +β) = 180º

α +β = 90º

Som beviser at ABC -trekanten har en indre vinkel på 90º og derfor er en riktig trekant.

Eksempel

I den følgende figuren er trekanten ABC isosceles og rektangel (Isorektangle Triangle), og er omkretsen til omkretsen lik 25 cm. Hvor mye er AC- og AB -segmentene?

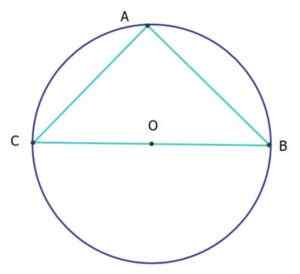
Omkretsen av omkretsen er dens lengde l, gitt avhengig av dens diameter d med formel:

L = πd

Derfor måler diameteren, som er CB -segmentet,:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Siden trekanten er isosceles, betyr dette at dens akutte vinkler måler 45º hver. Ettersom hypotenusen til trekanten er diameteren på omkretsen, kan et trigonometrisk forhold på 45 brukes, for eksempel:

Sen 45º = AC/CB

AC = CB × sin 45º = 7.96 cm × sin 45º = 5.64 cm

Kan tjene deg: Moivre teorem

AB -siden har samme mål: 5.64 cm, siden trekanten er isosceles.

Slike teorem -applikasjoner

Den første slike teorem kan brukes til å kjenne avstander som ikke er lett målbare. Det sies at slike reiste til Egypt og der bestemte, på en veldig genial måte, høyden på den store pyramiden.

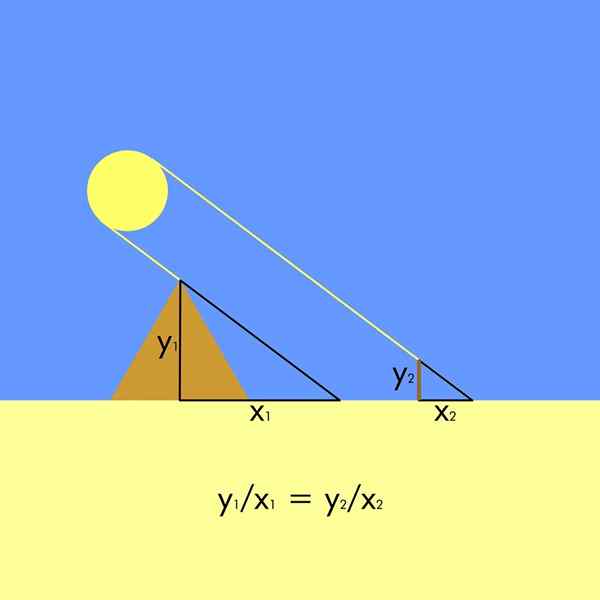
For dette var det nødvendig. Dermed dannes to lignende trekanter, siden solstrålene har parallell forekomst.

I figuren er pyramidenens høyde og1 Og skyggen hans er x1, Mens høyden på staven er og2 (Noen kronikere hevder at slike brukte sin egen høyde) og skyggen deres er x2. Ettersom trekantene er like, dannes følgende proporsjonalitetsforhold:

Å være veldig lett å fjerne høyden på pyramiden og1:

og1 = x1∙ (og2 ÷ x2)

Referanser

  1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
  2. Requena, b. Slikt teorem. Gjenopprettet fra: Universoformulas.com.
  3. Matematisk hall. Tales de Mileto og den store pyramiden. Hentet fra: Salonmatematisk.com
  4. Superprof didaktisk materiale. Miletus slikt. Gjenopprettet fra: Superprof.er.
  5. Thales og likhetsteorem. To veldig gamle problemer. Gjenopprettet fra: Edu.Xunta.Gal.