Thévenin Theorem hva som består, applikasjoner og eksempler

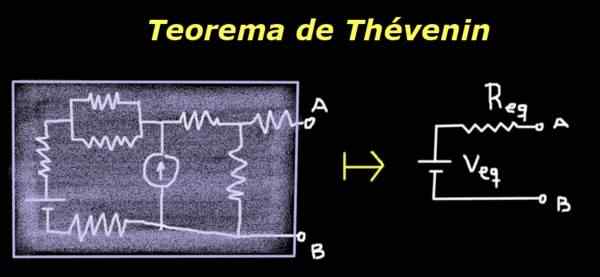
Han Thévenin teorem Den sier at en krets med terminal A og B kan erstattes av en ekvivalent som består av en kilde og en seriemotstand, hvis verdier gir samme potensielle forskjell mellom A og B og samme impedans som den opprinnelige kretsen.

Dette teoremet ble utgitt i 1883 av den franske ingeniøren Léon Charles Thévenin, men det hevdes at han ble oppgitt tretti år før av den tyske fysikeren Hermann von Helmholtz.

Figur 1. Thévenin teorem. Kilde: Selvlaget

Nytten ligger i det faktum at selv om den opprinnelige kretsen er sammensatt eller ukjent, for en belastning eller impedans som er plassert mellom terminalene A og B, oppfører den enkle ekvivalente kretsen til tévenin seg på samme måte som originalen.

[TOC]

Hvordan beregnes den ekvivalente spenningen trinn for trinn?

Spenningen eller potensialforskjellen på den ekvivalente kretsen kan oppnås på følgende måter:

- Eksperimentelt

Oppnå den ekvivalente spenningen til thévenin

Hvis det er en enhet eller utstyr som er i en "svart boks", måles potensialforskjellen mellom terminalene A og B med et voltmeter eller et oscilloskop. Det er veldig viktig at ingen belastning eller impedans mellom terminalene A og B plasseres. 

Et voltmeter eller et oscilloskop representerer ikke noen belastning for terminalene, siden begge lag har en veldig stor (ideelt uendelig) impedans og ville være som om terminalene A og B var uten belastning. Spenningen eller spenningen oppnådd på denne måten er den tilsvarende spenningen til thévenin.

Oppnå den ekvivalente impedansen av thévenin

For å oppnå ekvivalent impedans fra en eksperimentell måling, plasseres en motstand kjent mellom A- og B -terminalene og spenningsfallet eller spenningssignalet med et oscilloskop måles. 

Fra spenningsfallet i motstanden som er kjent blant terminalene, kan strømmen som sirkulerer gjennom den oppnås. 

Produktet av strømmen oppnådd med den ekvivalente motstanden pluss det målte spenningsfallet i den kjente motstanden er lik den ekvivalente spenningen til thévenin som tidligere er oppnådd. Fra denne likheten blir tilsvarende impedans av thévenin fjernet.

- Løse kretsen

Thévenins tilsvarende spenningsberegning

For det første kobles all belastning eller impedans av terminalene A og B koblet fra.

Som kretsen er kjent, blir masken eller Kirchhoffs lover brukt for å finne spenningen i terminalene. Denne spenningen vil være Thévenins ekvivalent.

Kan tjene deg: Mount Olympus (Mars)

Thévenins tilsvarende impedansberegning

For å få den tilsvarende impedansen, fortsetter vi til:

- Bytt ut de originale kretsspenningskildene med korte kretser "null impedans" og kildene til original krets for åpen "uendelig impedans".

- Deretter beregnes den tilsvarende impedansen etter reglene for serieimpedans og impedanser parallelt.

Thévenin Theorem Applications (del I)

Vi vil bruke Thévenins teorem for å løse noen kretsløp. I denne første delen vurderer vi en krets som bare har spenningskilder og motstander.

Eksempel 1 (beregning av tilsvarende spenning trinn for trinn)

Figur 2 viser kretsen som er i en himmelboks som har to batterier med elektromotorisk kraft V1 og V2 og motstander R1 og R2, kretsen har terminal A og B som en belastning kan kobles til.

Figur 2. Eksempel 1 av Thévenin -teorem. Kilde: Selvlaget

Målet er å finne den tilsvarende kretsen til thévenin, det vil si bestemme VT- og RT -verdiene til den ekvivalente kretsen.  Bruk følgende verdier: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω og R = 1Ω.

Steg for steg

Trinn 1 

Vi vil bestemme spenningen i terminalene A og B når de ikke er plassert noen belastning.

Steg 2

Kretsen som skal løses består av et enkelt nett som en strøm i sirkulerer som vi har tatt positivt i klokken.

Trinn 3

Vi reiser nettet og starter med nedre venstre hjørne. Ruten fører til følgende ligning:

V1 - I*R1 - I*R2 - V2 = 0

Trinn 4

Vi tømmer nettstrømmen jeg og oppnår:

I = (v1 -v2) / (r1 +r2) = (4v - 1v) / (3Ω +6Ω) = ⅓ a

Trinn 5

Med nettstrømmen kan vi bestemme spennings- eller spenningsforskjellen mellom A og B, som er:

VAB = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V

Det vil si at Thevenins tilsvarende spenning er: VT = 3V.

Trinn 6 (Thévenin -ekvivalent motstand)

Vi fortsetter nå med å beregne Thévenins tilsvarende motstand, som og som tidligere sagt, spenningskilder erstattes av en kabel.

I så fall har vi bare to motstand parallelt, så Thévenins tilsvarende motstand er:

RT = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω

Eksempel 1B (strømstrøm ved bruk av thévenin -ekvivalenten)

Koble til som belastning til terminalene A og B a motstand r = 1Ω til den ekvivalente kretsen og finn strømmen som sirkulerer gjennom nevnte belastning. 

Kan tjene deg: rettlinjet bevegelse: egenskaper, typer og eksempler

Løsning

Når motstanden r er koblet til den ekvivalente kretsen til thevenin, er det en enkel krets som består av en VT -kilde en seriemotstand i serie med motstand R. 

Vi vil kalle strømmen som sirkulerer gjennom belastningen R, slik at nettligningen er slik:

VT - IC* RT - IC* r = 0

Hvorfra det følger at IC er gitt av:

IC = VT / (RT + R) = 3V / (2Ω + 1Ω) = 1 A

Thévenin Theorem Verification

For å bekrefte at Thévenins teorem er oppfylt, kobler du til den opprinnelige kretsen og finner strømmen som sirkulerer ved å bruke loven om masker på den resulterende kretsen.

Den resulterende kretsen gjenstår og dens nettlikninger er som vist i følgende figur:

Figur 3. Mesh -strømmer. (Egen utdyping)

Legge til nettlikningene, er det mulig å finne nettstrømmen i1 avhengig av strøm I2. Deretter erstattes den i den andre nettlikningen, og det er en ligning med I2 som den eneste ukjente. Følgende tabell viser operasjoner.

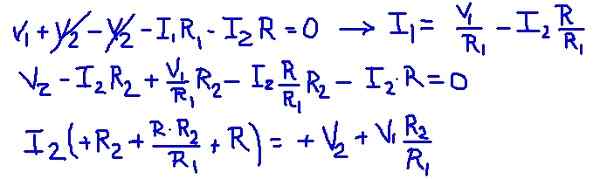Figur 4. Detaljer av operasjoner. (Egen utdyping)

Deretter erstattes motstandsverdiene og spenningene til kildene, og oppnår den numeriske verdien av I2 -nettstrømmen.

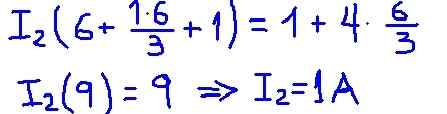Figur 5. Resultatdetalj. (Egen utdyping)

I2 -nettstrømmen er strømmen som sirkulerer gjennom belastningsmotstanden r og verdien funnet fra 1 A sammenfaller fullstendig med det som tidligere ble funnet med den ekvivalente kretsen til thévenin.

Anvendelse av Thévenins teorem (del II)

I denne andre delen vil Thévenins teorem bli brukt i en krets som har spenningskilder, gjeldende kilde og motstand. 

Eksempel 2A (Thévenin -ekvivalent motstand)

Målet er å bestemme den ekvivalente kretsen for thévenin som tilsvarer kretsen for følgende figur, når terminalene er uten motstanden til 1 ohmio, så plasseres motstanden og strømstrømmen bestemmes av den samme.

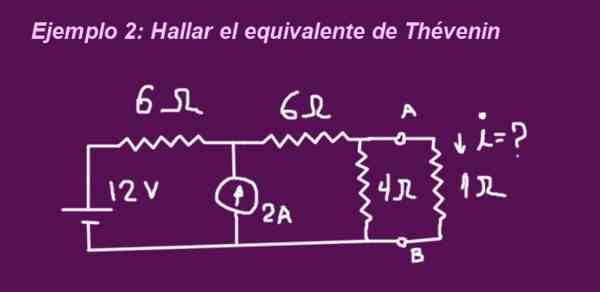Figur 6. Eksempel 2 krets. (Egen utdyping)

Løsning

For å finne den tilsvarende motstanden fjernes belastningsmotstanden (i dette tilfellet av 1 ohmio). I tillegg erstattes spenningskilder av en kortslutning og strømkilder med en åpen krets. 

På denne måten er kretsen som den tilsvarende motstanden blir beregnet den som er vist nedenfor:

Kan tjene deg: Boltzmann konstant: Historie, ligninger, beregning, øvelser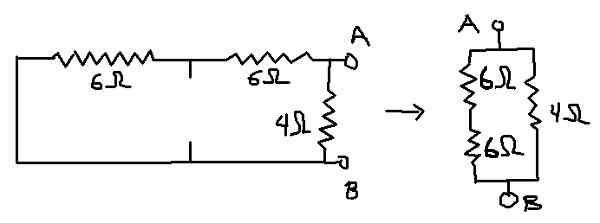Figur 7. Detalj for beregning av tilsvarende motstand (egen utdyping)

Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω som er den tilsvarende motstanden til thevenin (rth).

Eksempel 2B 

Beregn Thévenins tilsvarende spenning.

Løsning

For å beregne den ekvivalente spenningen til Thévenin vurderer vi følgende krets, der vi vil plassere strømningene i I1 og I2 i grenene som er angitt i følgende figur:

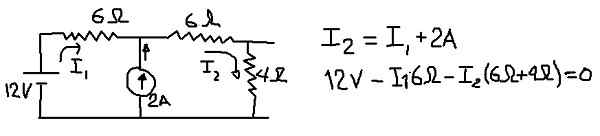Figur 8. Detaljer for beregning av thévenins spenning. (Egen utdyping)

I forrige figur er ligningen for gjeldende noder og spenningsligningen vist når det ytre nettet blir reist. Fra det andre av ligningene er den nåværende i1 fjernet:

I1 = 2 - I2*(5/3)

Denne ligningen erstattes i noder -ligningen:

I2 = 2 - (5/3) i2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A

Dette betyr at spenningsfallet i 4 ohm motstand er 6 volt.

Kort sagt, Thévenins spenning er VTH = 6 V.

Eksempel 2C

Finn den tilsvarende kretsen av thevenin og strøm i belastningsmotstanden.

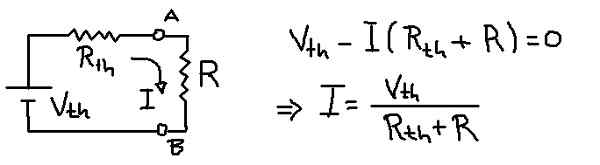Figur 9. Strøm i belastning med thévenin -ekvivalent. (Egen utdyping)

Løsning

Den forrige figuren viser den tilsvarende kretsen til thévenin med belastningsmotstanden r. Fra spenningsligningen i nettet er strømmen i som sirkulerer gjennom belastningsmotstanden r trukket.

I = VTH / (RTH + R) = 6V / (3Ω + 1Ω) = 1,5 A

Anvendelse av Thévenins teorem (del III)

I denne tredje delen av Thévenins teorem -applikasjon, inneholder en vekselstrømkrets en vekslende spenningskilde, en kondensator, induktans og motstand vurderes. 

Eksempel 3

Målet er å finne den tilsvarende thévenin -kretsen til følgende krets:

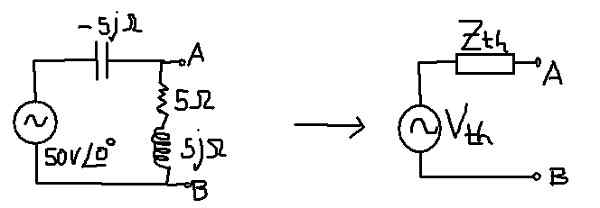Figur 10. Thévenin i en vekselstrømskrets. (Egen utdyping)

Løsning

Den ekvivalente impedansen tilsvarer den for kondensatoren parallelt med kombinasjon av motstands- og induktansserie.

Det inverse av den tilsvarende impedansen er gitt av:

Zeq^-1 = (-5j)^-1 + (5 + 5J)^-1 = (1/5) J + ((1/10 + (1/10) J) = (1/10 + 3/ 10 J) MHO

Og den tilsvarende impedansen vil da være:

Zeq = (1 - 3 j) ohm

Den komplekse strømmen jeg kan trekkes ut fra nettligningen:

50Vral0 - I (-5 J + 5 + 5J) = 50V∠0 - I*5 = 0 ===> I = 10A ∠0 

Nå beregnes spenningsfallet i motstand pluss induktans, det vil si VAB -spenningen som vil være den tilsvarende spenningen til thévenin:

VAB = I * (5 + 5 J) ω = 10A ∠0 * 5Ω ire45º = 50V hal5º

Med andre ord

Referanser

1. Elektroniske opplæringsprogrammer, Thevenins teorem. Gjenopprettet fra: elektronikk-tormales.Ws
2. Nettverksteori Spørsmål og svar. Thevenins teorem. Gjenopprettet fra: Sanfoundry.com
3. Thevenins teorem. Trinn for trinnprosedyre. Gjenopprettet fra: Elektrictchnology.org
4. Thevenins teorem. Løst eksempel trinn for trinn. Hentet fra: ElecticalSimple.Blogspot.com
5. Workshop om Thevenins og Nortons teoremer. Hentet fra: Web.IIT.Edu
6. Wikipedia. Thévenin teorem. Gjenopprettet fra: Wikipedia.com