Varignon teorem

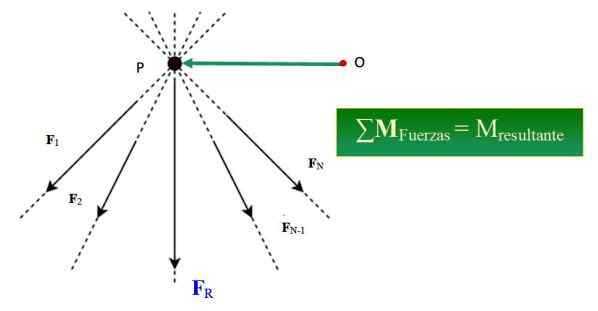
Figur 1.- Varignons teorem bekrefter at summen av styrkenes øyeblikk rundt et bestemt punkt tilsvarer resultatets tid med hensyn til det punktet. Kilde: Wikimedia Commons/F. Zapata.

Hva er Varignons teorem?

Varignons teorem uttaler i mekanikk at summen av øyeblikkene produsert av et system med samtidig krefter med hensyn til et bestemt punkt, er lik øyeblikket av den resulterende kraften med hensyn til samme punkt.

Av denne grunn er dette teoremet også kjent som Begynnelsen av øyeblikkene.

Mens den første som uttalte at det var nederlenderen Simon Stevin (1548-1620), var skaperen av det hydrostatiske paradokset, den franske matematikeren Pierre Varignon (1654-1722) den som senere ga ham sin endelige form.

Et eksempel på hvordan Varignons teorem fungerer i mekanikk er som følger: Anta at et enkelt system med to koplaner og samtidige krefter virker på et punkt F₁ og F₂, (Betegnet med fet skrift for vektorkarakter). Disse styrkene gir opphav til en netto eller resulterende kraft, kalt F_R.

Hver kraft utøver et dreiemoment eller øyeblikk med hensyn til et punkt eller, som beregnes av vektorproduktet mellom posisjonsvektoren r_Op og Strengh F, hvor r_Op Det er rettet fra eller til samtidig samtidig P:

M_O1 = r_Op × F₁

M_O2 = r_Op × F₂

Gitt F_R = F₁ + F₂, så:

M_ENTEN = r_Op × F₁ + r_Op × F₂ = M_O1 + M_O2

Men hvordan r_Op Det er en vanlig faktor, da å bruke distribusjonseiendom på kryssproduktet:

M_ENTEN = r_Op × (F₁ + F₂) = r_Op × F_R                

Derfor er summen av øyeblikkene eller dreiemomentene til hver kraft med hensyn til punktet eller tilsvarer tiden for den resulterende kraften med hensyn til samme punkt.

Uttalelse og demonstrasjon

Være et system med n samtidig krefter, dannet av F₁, F₂, F₃.. F_N, hvis handlingslinjer er ment på punkt P (se figur 1), øyeblikket for dette krefter systemet M_ENTEN, Angående et punkt eller er gitt av:

Kan tjene deg: ustabil balanse: konsept og eksempler

M_ENTEN = r_Op × F₁ + r_Op × F₂ + r_Op × F₃ +.. r_Op × F_N = r_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstrasjon

For å demonstrere teoremet er den distribuerende egenskapen til vektorproduktet mellom vektorer laget.

Være kreftene F₁, F₂, F₃.. F_N brukt på poeng på₁, TIL₂, TIL₃… TIL_N og samtidig på punkt P. Det resulterende øyeblikket av dette systemet, med hensyn til et punkt eller, kalt M_ENTEN, Det er summen av øyeblikkene til hver styrke, med hensyn til det punktet:

M_ENTEN = ∑ r_Oai × F_Yo

Der summen går fra i = 1 til i = n, siden det er n krefter. Siden dette er samtidig krefter, og siden vektorproduktet mellom parallelle vektorer er null, hender det at:

r_Pai × F_Yo = 0

Med nullvektoren betegnet som 0.

Øyeblikket til en av styrkene angående O, for eksempel makt F_Yo Anvendt i en_Yo, Det er skrevet slik:

M_{jeg hørte} = r_Oai × F_Yo

Posisjonsvektoren r_Oai  Det kan uttrykkes som summen av to vektorerposisjoner:

r_Oai = r_Op + r_Pai

På denne måten øyeblikket med hensyn til eller tvang F_Yo er:

M_{jeg hørte} = (r_Op + r_Pai) × F_Yo = (r_Op × F_Yo) + (r_Pai × F_Yo)

Men siste periode er null, som forklart ovenfor, fordi r_Pai er på handlingslinjen til F_Yo, derfor:

M_{jeg hørte} = r_Op × F_Yo

Å vite at systemets øyeblikk med hensyn til punkt eller er summen av alle de enkelte øyeblikkene for hver kraft med hensyn til det punktet, da:

M_ENTEN = ∑ M_{jeg hørte} = ∑ r_Op × F_Yo

Som r_Op Det er konstant kommer ut av summen:

M_ENTEN = r_Op × (∑ F_Yo)

Men ∑ F_Yo Det er ganske enkelt det resulterende nettet eller styrken F_R, Derfor konkluderes det umiddelbart med at:

Kan tjene deg: Leyden flaske: Deler, drift, eksperimenter

M_ENTEN = r_Op × F_R

Eksempel

Varignons teorem letter beregningen av maktmomentet F Når det gjelder punktet eller strukturen som er vist på figuren, hvis kraften er delt opp i dets rektangulære komponenter og øyeblikket for hver av dem beregnes:

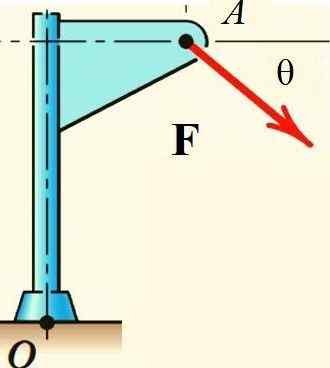Figur 2.- Varignons teorem gjelder for å beregne maktmomentet rundt eller. Kilde: f. Zapata.

Varignon Teorem -applikasjoner

Når styrken som følge av et system er kjent, kan Varignons teorem brukes for å erstatte summen av hvert av øyeblikkene produsert av kreftene som utgjør den på tidspunktet for det resulterende.

Hvis systemet består av krefter på samme plan og punktet med hensyn til hvilke du vil beregne øyeblikket tilhører det planet, er det resulterende øyeblikket vinkelrett.

For eksempel, hvis alle krefter er i XY -planet, er øyeblikket rettet mot Z -aksen og gjenstår bare for å finne dens størrelse og dets betydning, slik er tilfellet med eksemplet beskrevet ovenfor.

I så fall tillater Varignons teorem å beregne øyeblikket som følge av systemet gjennom summeringen. Det er veldig nyttig når det gjelder et system med tre -dimensjonale krefter, som retningen for det resulterende øyeblikket ikke er kjent.

For å løse disse øvelsene er det praktisk.

Trening løst

Ved Varignons teorem, beregne momentet Fain F rundt punktet eller vist på figuren hvis størrelsen på F er 725 n.

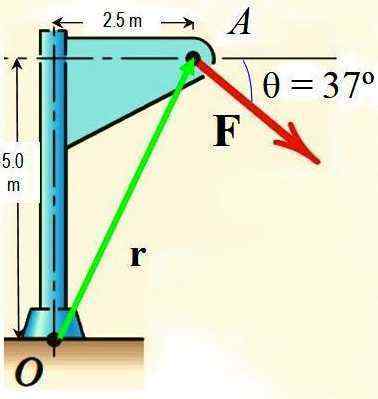Figur 3.- Figur for øvelsen løst. Kilde: f. Zapata.

Løsning

For å bruke Varignons teorem, dekomponerer kraft F i to komponenter, hvis respektive øyeblikk rundt eller blir beregnet og lagt til for å oppnå det resulterende øyeblikket.

Kan tjene deg: stiv kropp

F_x = 725 n ∙ cos 37 º = 579.0 n

F_og = - 725 n n ∙ Sen 37 º = −436.3 n

Tilsvarende posisjonsvektoren r Regissert fra eller til A har komponentene:

r_x = 2.5m

r_og = 5.0 m

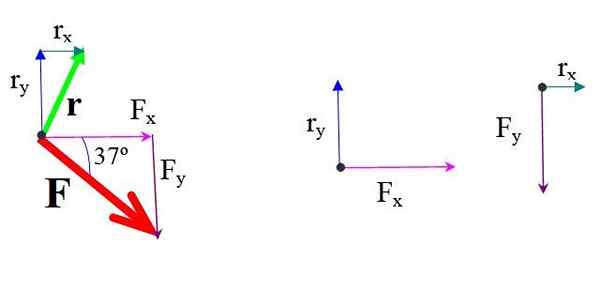Figur 4.- Kraft- og posisjonskomponenter. Kilde: f. Zapata.

Øyeblikket for hver komponent av kraften med hensyn til eller multipliserer kraften og vinkelrett avstand.

Begge kreftene har en tendens til å rotere strukturen i samme retning, som i dette tilfellet er poengsummen, som vilkårlig tildelt positivt tegn:

M_Okse = F_x∙ r_og ∙ sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_og∙ r_x ∙ sin (−90º) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Det resulterende øyeblikket med hensyn til eller er:

M_ENTEN = M_Okse + M_Oy = 3985.8 n ∙ m vinkelrett på planet og i et dreiemoment.

Referanser

1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley. 
2. Øl, f. 2010. Statisk. McGraw Hill. 9na. Utgave.
3. Hibbeler, R. 1992. Mekanikk for ingeniører. 6. Utgave. Cecsa.
4. HK Engineering. Varignon teorem. Gjenopprettet fra: YouTube.com.
5. Wikipedia. Varignons teorem (mekanikk). Hentet fra: i.Wikipedia.org.