Forklaring Faktor teorem, eksempler, øvelser

Han Faktor teorem sier at et polynom P (x) er delbar med en binomial av formen (x - a) hvis x = a er en rot av p (x), det vil si P (a) = 0. Det sies at et polynom kan deles mellom hverandre når resten eller hvile er null.

Et polynom er et uttrykk for form:

P (x) = a_n xⁿ + til_N-1 x^N-1 +… + A₁ x + a₀

Figur 1. Faktor teorem. Kilde: f. Zapata.

Hvor:

-n er graden av polynom, og er det største heltallnummeret som den uavhengige variabelen X stiger,

-Verdier a_n, til_N-1 ,… + A₁ , til₀ De er koeffisientene til polynomet, som generelt er reelle tall, men de kan også være komplekse tall.

En grad N -polynom kan dekomponere som et produkt av formbinomialer:

(X - r_Yo)

Hvor r_Yo Det er i-alkish P (x) roten:

P (x) = a_n (X - r₁) (X - r₂) ... (x - r_n)

Siden antall røtter til et polynom er lik graden av det samme.

[TOC]

Eksempler

- Eksempel 1

Tenk på polynomet med sak:

P (x) = 3⋅x² - 7⋅x + 2

Du vil vite om dette polynomet er delbart med binomialen (x - 2). Hvis faktorsteoremet brukes, må vi evaluere P (x = 2) for å vite om verdien 2 er en rot eller ikke er. Vi fortsetter deretter med å evaluere uttrykket:

P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.

Det viser seg at x = 2 er p (x) rot, så i henhold til faktorsteoremet er binomialen (x - 2) faktisk en faktor på p (x).

La oss gå videre til direkte verifisering som gjør divisjonen. Detaljene om hvordan divisjonen gjøres vises i følgende figur:

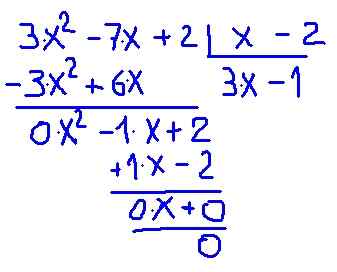Figur 2.- Polynomavdeling P (x) mellom binomial x-2. Kilde: f. Zapata.

Det er bekreftet at kvotienten mellom P (x) og (x -2) gir et polynom av en mindre grad kalt kvotienten C (x) = 3⋅x - 1 med rest 0.

Kan tjene deg: vektorfunksjoner

Vi kan oppsummere resultatet som følger:

(3⋅x² - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0

Det forrige uttrykket kan skrives på en annen måte, og husker ganske enkelt at utbyttet P (x) er lik produktet fra divisoren (x -2) med kvotienten (3⋅x - 1) pluss resten (null i dette tilfellet ):

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0

På denne måten skriver P (x) polynomet (x), det vil si et produkt av polynomer, det originale polynomet: det originale polynomet:

(3⋅x² - 7⋅x + 2) = (x -2) (3⋅x - 1)

- Eksempel 2

Være polynomet q (x) = x³ - x + 2. Du vil vite om det er delbart med binomialen (x + 1).

Den mest direkte måten er ganske enkelt å bruke faktorsteorem. I dette tilfellet må du ganske enkelt bekrefte om x = -1 annuller eller ikke polynomet Q (x).

Vi fortsetter ved å erstatte:

Q (-1) = (-1)³ - (-1) + 2 = -1 + 1 + 2 = 2

Resultatet er forskjellig fra null, derfor sikrer faktorsteoremet at polynom q (x) ikke er delbar mellom (x + 1), siden q (-1) ≠.

Nå vil delingen av Q (x) bli gjort mellom binomialen (x + 1) som en metode for verifisering av vår konklusjon.

Ved denne anledningen vil divisjonen bli utført gjennom den syntetiske divisjonsmetoden, som består av å plassere i topp -gradering første klasse rad alle koeffisientene til polynomet, inkludert de manglende, siden de har null koeffisient.

Så i den første kolonnen blir den uavhengige betegnelsen på divisoren plassert, men med skiltet endret, i vårt tilfelle er divisoren (x + 1). Den uavhengige uttrykket er 1, men som i den første kolonnen er den plassert endret tegn, det vil si -1.

Følgende figur illustrerer hvordan den syntetiske inndelingen utføres:

Kan tjene deg: Polynomligninger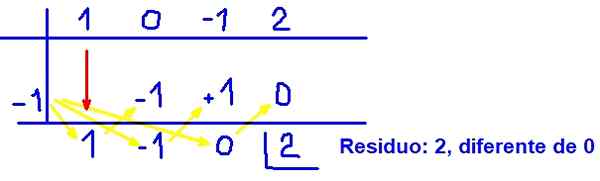Figur 3. Eksempel på polynomisk syntetisk inndeling. Kilde: f. Zapata.

Med dette resultatet er det bevist at (x + 1) det ikke er en faktor av polynom q (x) = x³ - x + 2 Siden resten ikke er null.

Denne konklusjonen er ikke overrasket, fordi den allerede hadde blitt spådd med faktorsteoremet. Merk at når du erstatter x = -1 i q (x), er det som oppnås nettopp resten eller resten av polynomavdelingen, siden q (-1) = rest = 2.

Divisjonen gir selvfølgelig tilleggsinformasjon om kvotient C (x) = x² - x.

Husker at utbytte q (x) er lik divisoren (x + 1) med forhold C (x) pluss resten r = 2 har vi utvidelsen av polynomet Q (x) som følger:

Q (x) = (x + 1) (x² - x) + 2 = x (x + 1) (x - 1) + 2

Det skal bemerkes at dette uttrykket ikke er faktoriseringen av nevnte polynom, siden det er et ikke -null -betegnelse, som nettopp er verdien av verdi 2.

Øvelser

- Oppgave 1

Finn polynomfaktorene

P (x) = x³ - 5 x² + 2 x + 8

Og skriv også din faktorisering.

Løsning

Faktor teorem indikerer at vi må se etter røttene til og finn deretter faktorene (x - til), I dette tilfellet, ettersom det er en polynom i grad tre, må det være tre røtter. 

Siden det er et polynom med hele koeffisienter, må røttene være blant delingene av det uavhengige begrepet at i dette tilfellet er 8. Disse delingene er:

± 1, ± 2, ± 4, ± 8.

Vi begynner med å utforske +1: P (+1) = 1³ - 5⋅ 1² + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 som er forskjellig fra 0, er derfor ikke rot.

Vi utforsker -1:

P (-1) = (-1)³ - 5⋅ (-1)² + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0

Fra resultatet er det konkludert med at -1 er roten til P (x) y (x -( -1)) = (x + 1) er en polynomfaktor.

Kan tjene deg: minimums torg

Vi må finne ytterligere to faktorer:

Vi prøvde den neste som er +2:

P (+2) = (+2)³ - 5⋅ (+2)² + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0

Igjen får vi null. Da er den andre faktoren (x - 2).

Siden det er en polynom i grad tre, trenger vi bare å finne en faktor. Nå prøvde vi +4 -verdien å vite om polynomet kansellerer:

P (+4) = (+4)³ - 5⋅ (+4)² + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.

Med andre ord.

Du trenger ikke å fortsette å lete etter, fordi det er et polynom i grad 3 som har tre røtter på det meste. I denne øvelsen viste alle røttene seg å være ekte og hel.

Derfor er polynomen P (x) faktor som dette:

P (x) = x³ - 5 x² + 2 x + 8 = (x + 1) (x - 2) (x - 4).

- Oppgave 2

Være p⋅x -polynomet³ - x + 2p. Bestem verdien av P for at polynom kan deles med (x + 2).

Løsning

Vi bruker faktorsteoremet, som sier at hvis x = -2 avbryter polynomet da (x -( -2)) er en faktor av nevnte polynom.

Deretter blir X erstattet av (-2) i det opprinnelige polynomet, det er forenklet og tilsvarer null:

P⋅ (-2)³ - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0

Nå blir verdien av P ryddet slik at likhet blir oppfylt til null:

P = -2 / 10 = -⅕ 

Dette betyr at polynom: 

-⅕⋅x³ - X - ⅖

Det er delbart med (x + 2), eller det som er tilsvarende: (x + 2) er en av faktorene.

Referanser

1. Baldor Aurelio. Algebra. Patria redaksjonell gruppe.
2. Demana, w. Precáculculo: grafisk, numerisk, algebraisk 7. ed. Pearson Education.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.