Fysisk

Newtons tredje lovapplikasjoner, eksperimenter og øvelser

Newtons tredje lovapplikasjoner, eksperimenter og øvelser

De Newtons tredje lov, også kalt Handlingslov og reaksjon Han bekrefter at når et objekt utøver styrke over en annen, utøver den sistnevnte også på den første en kraft av like stor størrelse og retning og motsatt forstand.

Isaac Newton ga ut sine tre lover i 1686 i sin bok Philosophiae Naturalis Principia Mathematica eller matematiske prinsipper for naturfilosofi.

En romrakett mottar den nødvendige fremdriften takket være gassene som ble utvist. Kilde: Pixabay.

[TOC]

Forklaring og formler

Den matematiske formuleringen av Newtons tredje lov er veldig enkel:

F12 = -Ftjueen

En av styrkene kalles handling Og den andre er den reaksjon. Imidlertid er det nødvendig å fremheve viktigheten av denne detaljene: Begge handler på forskjellige objekter. De gjør det også samtidig, selv om denne terminologien feil antyder at handlingen oppstår før og reaksjonen etter.

Siden krefter er vektorer, betegner de med fet skrift. Denne ligningen indikerer at det er to objekter: objekt 1 og objekt 2. Kraften F12 Det er den som utøver objekt 1 på objekt 2. Kraften Ftjueen utøves av objekt 2 på objekt 1. Og tegnet (-) påpeker at de er imot.

Når du nøye observerer Newtons tredje lov, er det en viktig forskjell med de to første: Mens de påkaller et enkelt objekt, refererer den tredje loven til to forskjellige objekter.

Og hvis du tenker nøye, krever interaksjoner par av objekter.

Det er grunnen til at kreftene til handling og reaksjon ikke blir kansellert eller balansert, selv om de har samme størrelse og retning, men ellers: de brukes i forskjellige kropper.

applikasjoner

Ballinteraksjon - Jorden

Her er en veldig daglig anvendelse av et samspill relatert til Newtons tredje lov: en ball som faller vertikalt og jorden. Ballen faller til bakken fordi jorden utøver en tiltrekningskraft, som er kjent som tyngdekraften. Denne styrken får ballen til å falle med konstant akselerasjon på 9.8 m/s2.

Imidlertid tenker nesten ingen på det faktum at ballen også utøver en tiltrekningskraft på jorden. Selvfølgelig forblir jorden uforanderlig, fordi massen er mye større enn ballen og opplever derfor en foraktelig akselerasjon.

En annen bemerkelsesverdig sak om Newtons tredje lov er at kontakten mellom de to objektene som samhandler ikke er nødvendig. Det er tydelig med eksemplet som nettopp er blitt sitert: ballen tar fremdeles ikke kontakt med jorden, men likevel utøver den attraksjonen uansett. Og ballen på jorden også.

En kraft som tyngdekraft, som virker om hverandre både hvis det er kontakt mellom objekter som om det ikke er noe navn på "Distance Action Force". I stedet krefter som friksjon og normal, krever de at objektene som samhandler er i kontakt, slik at de kalles "kontaktkrefter".

Formler hentet fra eksemplet

Tilbake til et par ballobjekter - Jorden, velge P -rater for ballen og T for jorden og anvende Newtons andre lov til hver deltaker i dette systemet oppnås:

Det kan tjene deg: Diskret variabel: Karakteristikker og eksempler

Fresulterende = m.til

Den tredje loven uttaler at:

mPtilP = - mTtilT

tilP = 9.8 m/s2 rettet vertikalt ned. Siden denne bevegelsen foregår langs den vertikale retningen kan dispenseres med vektornotasjonen (BOLD); Og å velge retningen opp som positiv og ned som negativ, har du:

tilP = 9,8 m/s2

mT ≈ 6 x 10 24 Kg

Uavhengig av massen på ballen, er jordens akselerasjon null. Det er derfor det observeres at ballen faller mot jorden og ikke omvendt.

Drift av en rakett

Rakettene utgjør et godt eksempel på anvendelse av Newtons tredje lov. Raketten vist på bildet i begynnelsen stiger takket være fremdrift av varm gass i høy hastighet.

Mange tror at dette skjer fordi disse gassene på en eller annen måte "støtter" atmosfæren eller på bakken for å støtte og skyve raketten. Det fungerer ikke slik.

Når raketten utøver styrke på gassene og utvider dem tilbake, utøver gassene en kraft på raketten, som har samme modul, men motsatt retning. Denne styrken er den som gir raketten sin akselerasjon opp.

Hvis du ikke har en rakett av disse for hånd, er det andre måter å bekrefte at Newtons tredje lov fungerer for å gi fremdrift. Vannraketter kan bygges, der det nødvendige drivkraften tilbys av vannet per trykkgass.

Det skal bemerkes at starten av en vannrakett tar tid og krever mange forholdsregler.

Bruk av skøyter

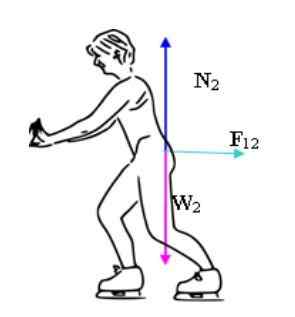
En rimeligere og umiddelbar måte å bekrefte effekten av Newtons tredje lov er å sette et par skøyter og fremme en vegg.

Det meste av tiden evnen til å utøve makt med gjenstander som er i bevegelse er assosiert, men sannheten er at immobile gjenstander også kan utøve styrke. Skateren er kjørt tilbake takket være styrken som den bevegelsesløse utøver på den.

Kontaktoverflater utøver kontaktkrefter (normalt) med hverandre. Når en bok støttes på et horisontalt bord, utøver den en normal vertikal kraft på den. Boken utøver på bordet en vertikal kraft av samme numeriske verdi og motsatt forstand.

Barneeksperiment: Skatere

Barn og voksne kan oppleve Newtons tredje lov og bekrefte at handlings- og reaksjonskrefter ikke er annullert og er i stand til å gi bevegelser.

To skatere på isen eller på en veldig glatt overflate kan drives hver.

Tenk på to skatere med ganske annen deig. De er midt i en skøytebane med foraktelig friksjon og er opprinnelig i ro. I et gitt øyeblikk skyver de hverandre på å bruke konstant styrke med håndflatene. Hvordan vil begge bevege seg?

Kan tjene deg: balanseringsvektor: beregning, eksempler, øvelserTo skatere er drevet midt på en skøytebane. Kilde: Benjamin Crowell (Wikipedia-bruker Bcrowell) [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Det er viktig å understreke at siden det er en overflate uten friksjon, er de eneste ubalanserte kreftene kreftene som skatere bruker hverandre. Mens vekten og normale handlingen på begge deler, er disse kreftene balansert, fra hva skatere ville akselerere i en vertikal retning.

Formler brukt i dette eksemplet

Newtons tredje lov uttaler at:

F12 = -Ftjueen

Det vil si at styrken utøvd av skater 1 på 2, er den samme i størrelsesorden som 2 utøver på 1, med samme retning og motsatt retning. Merk at disse kreftene blir brukt på forskjellige gjenstander, på samme måte som kreftene var på ballen og jorden i det forrige konseptuelle eksempelet.

m1 til1 = -M2 til2

Siden kreftene er motsatte, vil akselerasjonene som forårsaker også være, men deres størrelser vil være annerledes, fordi hver skater har en annen masse. La oss se på akselerasjonen ervervet av den første skateren:

Hvis massen til den første skater er større enn den andre, vil akselerasjonen være lavere. Dette er å forvente fordi det har større treghet. Den letteste skaterne skaffer seg større akselerasjon. Hvis massene er de samme, vil akselerasjonene også være.

Så bevegelsen som skjer nedenfor er separasjonen av begge skatere i motsatte sanser. I prinsippet var skatere i ro midt på sporet. Hver utøver en styrke på den andre som gir en akselerasjon mens hendene er i kontakt og skyvekraften varer.

Etter det beveger skaterne seg bort fra hverandre med ensartet rettlinjet bevegelse, ved ikke å oppføre ubalanserte krefter. Hastigheten til hver skater vil være annerledes hvis massene deres også er det.

Trening løst

For å løse problemer der Newtons lover må brukes, er det nødvendig å tegne kreftene som virker nøye på objektet. Denne tegningen kalles "gratis kroppsdiagram" eller "isolert kroppsdiagram". I dette diagrammet skal kreftene som kroppen utøver på andre objekter ikke vises.

Hvis det er mer enn ett objekt involvert i problemet, er det nødvendig.

1- Skatere fra forrige seksjon har respektive masser m1 = 50 kg og m2 = 80 kg. De skyver hverandre med en konstant kraft på 200 n. Skyvekraften har en varighet på 0.40 sekunder. Finne:

a) Akselerasjonen ervervet av hver skater takket være skyvekraften.

b) Hastigheten til hver enkelt når de skiller seg

Løsning

a) ta som en horisontal positiv adresse den som går fra venstre til høyre. Bruke Newtons andre lov med verdiene gitt av uttalelsen er:

Ftjueen = m1til1

Hvor fra:

For den andre skater:

b) For å beregne hastigheten som de bærer akkurat når de er separate, brukes de kinematiske ligningene av den jevnt akselererte rettlinjede bevegelsen:

Kan tjene deg: gjensidig induktans: formel/koeffisient, applikasjoner, øvelser

Den første hastigheten er 0, siden de var i ro midt på sporet:

vF = Kl

vF1 = a1t = -4 m/s2 . 0.40 s = -1.6 m/s

vF2 = a2T = +2.5 m/s2 . 0.40 s = +1 m/s

Resultater

Som forventet får person 1 lettere større akselerasjon og derfor raskere hastighet. Nå observer følgende om produktet av deigen på grunn av hastigheten på hver skater:

m1 v1 = 50 kg . (-1.6 m/s) = - 80 kg.m/s

m2 v2 = 80 kg . 1 m/s = +80 kg.m/s

Summen av begge produktene er 0. Produktet av massen etter hastighet kalles mengden bevegelse P. Det er en vektor med samme retning og hastighetsfølelse. Når skaterne var i ro og hendene i kontakt, kan det antas at de dannet det samme objektet hvis mengde bevegelse var:

Penten = (m1 +m2) venten = 0

Etter at skyvekraften er ferdig, forblir mengden bevegelse av skøytesystemet 0. Derfor bevares mengden bevegelse.

Eksempler på Newtons tredje lov i hverdagen

Gå

Walking er en av de mest daglige handlingene som kan utføres. Hvis nøye observert, krever gangaksjonen å skyve foten mot bakken, slik at den returnerer en lik og motsatt kraft på foten av rullatoren.

Da vi stadig anvendte Newtons tredje lov. Kilde: Pixabay.

Det er nettopp den kraften som lar folk gå. På flyturen utøver fuglene styrke på luften og luften skyver vingene slik at fuglen blir kjørt fremover.

Bevegelse av en bil

I en bil utøver hjulene styrke på fortauet. Takket være fortaureaksjonen, utøver den på dekkkreftene som driver bilen fremover.

Sport

I sportspraksis er handlings- og reaksjonskreftene mange og har en veldig aktiv deltakelse.

La oss for eksempel se atleten med foten støttet av en startblokk. Blokken gir en normal kraft som en reaksjon på skyvekraften som atleten utøver på den. Resultatet av denne normale og vekten av korridoren, resulterer i en horisontal kraft som gjør at idrettsutøveren kan kjøre fremover.

Idrettsutøveren bruker startblokken for å legge impuls fremover ved utgangen. Kilde: Pixabay.

Brannslanger

Et annet eksempel der Newtons tredje lov er til stede er i brannmenn som holder brannslanger. Slutten på disse store slangene har et håndtak på dysen som brannmannen må holde når vannstrålen kommer ut, for å unngå tilbakeslaget som oppstår når vannet kommer ut i full hastighet.

Av samme grunn er det praktisk.

Referanser

  1. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 80 - 82.
  2. Rex, a. 2011. Fundamentals of Physics. Pearson. 73 - 75.
  3. Tipler, s. 2010. Fysisk. Volum 1. 5. utgave. Redaksjon tilbake. 94 - 95.
  4. Stern, d. 2002. Astronomer til astronaves. Hentet fra: pwg.GSFC.gryte.Gov.