Teselados karakteristikk, typer (vanlige, uregelmessige), eksempler

De Tesselled De er overflater dekket av en eller flere figurer som heter Tessels. De er overalt: i gater og bygninger av alle slag. Tesseller eller fliser er flate stykker, vanligvis polygoner med kongruente eller isometriske eksemplarer, som er plassert etter et vanlig mønster. På denne måten er det ingen mellomrom uten å bli dekket, og flisene eller mosaikken overlapper ikke hverandre. 

I tilfelle at en enkelt type mosaikk dannet av en vanlig polygon brukes, er det en Vanlig Tesseld, Men hvis to eller flere typer vanlige polygoner brukes, er det en Semi -regulær tesselled.

Figur 1. Uregelmessige fliser på gulvet, fordi rektangler er ikke-regelmessige polygoner, selv når rutene er. Kilde: Pixabay.

Til slutt når polygonene som danner Tesseldo ikke er vanlige, så det er en uregelmessig tessell.

Den vanligste typen Tesseldo er den som er dannet av rektangulære og spesielt firkantede mosaikker. I figur 1 har vi et godt eksempel.

[TOC]

Historien om Teselados

Tessellasjon har blitt brukt i tusenvis av år for å dekke gulv og vegger av palasser og templer av forskjellige kulturer og religioner.

For eksempel den sumeriske sivilisasjonen som blomstret rundt 3500 til.C. Sør for Mesopotamia, mellom elvene Eufrat og Tigris, brukte de teselene i sin arkitektur.

Figur 2. Teselados sumerios ved døren til Istar. Kilde: Wikimedia Commons.

Tesels har også vekket interessen til matematikerne av alle tider: å starte med Archimedes i det tredje århundre f.Kr.

Det kan tjene deg: brøkdel tilsvarer 3/5 (løsning og forklaring)

Penrose skapte en ikke -periodisk tessellasjon kjent som Penrose Tessellation. OGdisse De er bare noen navn på forskere som bidro mye om Tessellation.

Vanlige tesels

Regelmessig teslate er laget med en enkelt type vanlig polygon. På den annen side, slik at Tesseldo kan betraktes som vanlig, må flyets punkt:

-Tilhører polygoninteriøret

-Eller til kanten av to tilstøtende polygoner 

-Til slutt kan det tilhøre den vanlige toppunktet til minst tre polygoner.

Med de ovennevnte begrensningene kan det påvises at bare de likesidelige trekantene, rutene og sekskantene kan danne et vanlig tessel.

Nomenklatur

Det er en nomenklatur for å betegne teselene som består av oppføring i retning av klokken nåler og atskilt med et punkt, antall sider av polygonene som omgir hver node (eller toppunkt) til Tesselled, alltid starter med det minste tallet av sider.

Denne nomenklaturen gjelder vanlige og semi -regulære tesselves. 

Eksempel 1: Triangular Teselado

Figur 3 viser en trekantet vanlig flis. Det skal bemerkes at hver trekantede fliseknute er den vanlige toppunktet til seks liksidige trekanter. 

Måten å betegne denne typen Tesseldo er 3.3.3.3.3.3, som også er betegnet med 3⁶.

Figur 3. Trekantet vanlig teselado 3.3.3.3.3.3. Kilde: Wikimedia Commons

Eksempel 2: Square Tessel

Figur 4 viser en vanlig flis bare sammensatt av firkanter. Det skal bemerkes at hver fliseknute er omgitt av fire kongruente firkanter. Notasjonen som gjelder denne typen firkantede tesselves er: 4.4.4.4 o vekselvis 4⁴

Figur 4. Square Tesseld 4.4.4.4. Kilde: Wikimedia Commons.

Eksempel 3: sekskantet tesseld

I en sekskantet tesselle. Nomenklaturen for en vanlig sekskantet Tesselled er 6.6.6 o Alternativt 6³.

Kan tjene deg: koniske seksjoner: Typer, applikasjoner, eksempler Figur 5. Sekskantet Tesseld 6.6.6. Kilde: Wikimedia Commons.

Semi -regulær tesselled

Semi -regulære eller tessellede tesels av Archimedes består av to eller flere typer vanlige polygoner. Hver node er omgitt av de typer polygoner som utgjør tesselleret i samme rekkefølge, og tilstanden til en kant som deles med naboen, opprettholdes.

Det er åtte semi -regulære tesels:

1. 3.6.3.6 (tri-heksagonal tesselled)
2. 3.3.3.3.6 (sekskantet Teslate Romo)
3. 3.3.3.4.4 (Elongado Triangular Teselado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (Rombi-tri-heksagonal Tesseld)
6. 4.8.8 (avkortet firkantet tesselled)
7. 3.12.12 (avkortet sekskantet Tesseld)
8. 4.6.12 (avkortet tri-heksagonal Tesseld)

Noen eksempler på semi -regulær teslate er vist nedenfor.

Eksempel 4: Tixagonal Teselado

Det er den som er sammensatt av vanlige liksidige trekanter i struktur 3.6.3.6, noe som betyr at en fliseknute er omgitt (til den fullfører en retur) med en trekant, en sekskant, en trekant og en sekskant. Figur 6 viser en slik tessel.

Figur 6. Tri-heksagonal tesseld (3.6.3.6) Det er et eksempel på semi -regulær tesselled. Kilde: Wikimedia Commons.

Eksempel 5: sekskantet Tesseldo Romo

I likhet med flisen i det forrige eksemplet, består dette også av trekanter og sekskanter, men distribusjonen rundt en node er 3.3.3.3.6. Figur 7 illustrerer tydelig denne typen Tesselled.

Figur 7. Den sekskantede Tesseldo Romo består av en sekskant omgitt av 16 trekanter i konfigurasjon 3.3.3.3.6. Kilde: Wikimedia Commons.

Eksempel 6: Rombi-tri-heksagonal tessel

Det er en flis som består av trekanter, firkanter og sekskanter, i konfigurasjon 3.4.6.4, som er vist i figur 8.

Figur 8. Semi -regulær tessellet sammensatt av en trekant, en firkant og en sekskant i konfigurasjon 3.4.6.4. Kilde: Wikimedia Commons.

Uregelmessige tesels

De kalles uregelmessige tesels til de som er dannet av uregelmessige polygoner, eller av vanlige polygoner, men som ikke oppfyller kriteriet om at en node er et toppunkt på minst tre polygoner.

Det kan tjene deg: Antiderivat: Formler og ligninger, eksempler, øvelser

Eksempel 7

Figur 9 viser et eksempel på uregelmessig fliser, der alle polygoner er vanlige og kongruente. Det er uregelmessig fordi en node ikke er en vanlig toppunkt på minst tre firkanter, og det er også nabobygninger som ikke helt deler en kant.

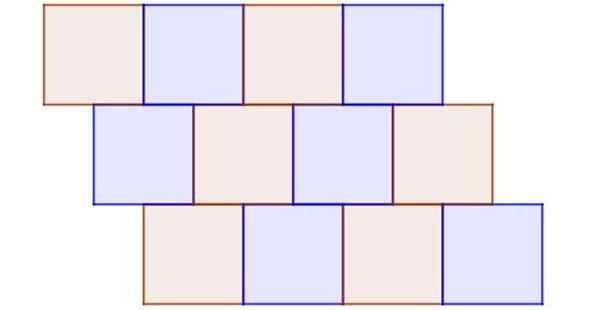Figur 9. Selv når alle fliser er kongruente firkanter, er dette et klart eksempel på uregelmessig tesselled. Kilde: f. Zapata.

Eksempel 8

Parallellogrammet tees en flat overflate, men med mindre det er et firkant ikke kan danne en vanlig tessel.

Figur 10. En Tesseldo dannet av parallellogrammer er uregelmessig, siden mosaikkene er ikke -regulære polygoner. Kilde: f. Zapata.

Eksempel 9

Ikke-regulære sekskanter med sentral symmetri satte en flat overflate, som vist i følgende figur:

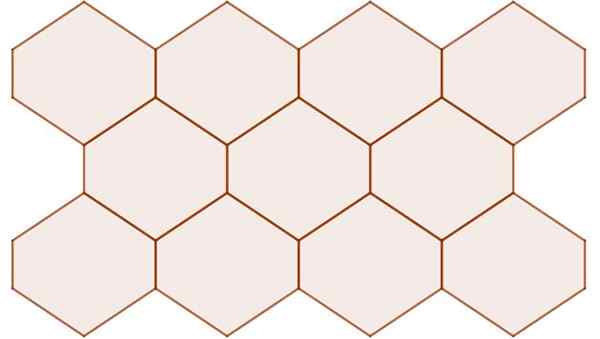Figur 11. Heksagoner med sentralsymmetri selv når de ikke er vanlig, setter de flyet. Kilde: f. Zapata.

Eksempel 10: El Cairo Teselado

Det er en veldig interessant tessellasjon, sammensatt av pentagoner med sider av like lengde, men med ulik vinkler, hvorav to er rette og de tre andre har 120º hver.

Hans navn kommer at denne Tesseld er i fortauet i noen av gatene i Kairo i Egypt. Figur 12 viser Tesseldo av Kairo.

Figur 12. Kairo Tesseldo. Kilde: Wikimedia Commons.

Eksempel 11: Teselado al-Andalus

Tesseldo under noen deler av Andalusia og Nord -Afrika er preget av geometri og epigrafi, i tillegg til prydelementer som vegetasjon. 

Palacios 'tesselled som Alhambra sammensatt av fliser dannet av keramiske biter av mange farger, med flere (for ikke å si uendelige) former som utløste geometriske tomter.

Figur 13. Teselado Palacio de la Alhambra. Tartaglia / Public Domain

Eksempel 12: Teselado i videogyrene

Også kjent som Tesellation, det er et av de mest boom i videospill. Dette er opprettelsen av teksturer for å simulere tesseldet til de forskjellige scenariene som vises i simulatoren.

Dette er den klare refleksjonen som disse dekslene fortsetter å utvikle seg ved å overføre virkelighetens grenser.

Referanser

1. Kos deg med matematikk. Tesels. Gjenopprettet fra: Nytmatimaticas.com
2. Rubiños. Tesels løste eksempler. Gjenopprettet fra: Matematikk.Blogspot.com
3. Weisstein, Eric w. "Deiregula Tessellation". Weisstein, Eric W, Ed. Mathworld. Wolfram Research.
4. Wikipedia. Tesselled. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Vanlig Tesseld. Gjenopprettet fra: er.Wikipedia.com