Balacket trekantegenskaper, egenskaper, formler, område

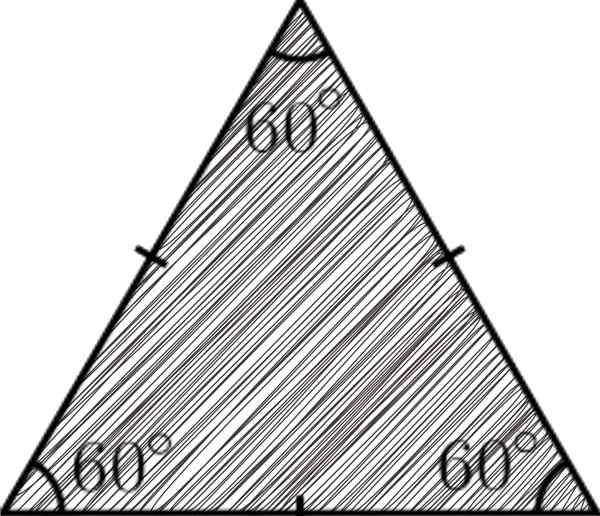
EN likesidet trekant Det er en tre -sidig polygon, der alle er de samme; det vil si at de har samme tiltak. For den egenskapen ble det gitt navnet likesidelig (like sider).

Trekantene er polygoner betraktet som de enkleste i geometri, fordi tre sider, tre vinkler og tre hjørner er dannet. Når det.

Et eksempel på den likesidelige trekanten

[TOC]

Kjennetegn på likevektstrekantene

- Like sider

De likestående trekantene er flate og lukkede figurer, sammensatt av tre linjer med linjer. Trekantene er klassifisert etter deres egenskaper, i forhold til deres sider og vinkler; Det likesidelige ble klassifisert ved å bruke målene på sidene som en parameter, siden disse er nøyaktig de samme, det vil si at de er kongruente.

Den likesidelige trekanten er et spesielt tilfelle av Isosceles -trekanten fordi to av sidene er kongruente. Det er grunnen til at alle de liksidige trekantene også er isosceles, men ikke alle isosceles -trekanter vil være likeverdige.

På denne måten har de likestående trekantene de samme egenskapene til en isosceles -trekant.

De likesidelige trekantene kan også klassifiseres ved amplituden av deres indre vinkler som en liksidig akutt trekant, som har alle tre sider og tre indre vinkler med samme mål. Vinklene vil være akutte, det vil si at de vil være mindre enn 90^enten.

- Komponenter

Trekanter generelt har flere linjer og punkter som komponerer det. De brukes til å beregne området, sider, vinkler, median, bisektor, mediatrix og høyde.

• Medianen: Det er en linje som forlater fra midtpunktet på den ene siden og når motsatt toppunkt. De tre mediene deltar på et punkt som heter baricentro eller centroid.
• Bisektoren: Det er en semi -rett som deler vinkelen til toppunktet i to vinkler med like mål, så det er kjent som symmetriakse. Den likesidelige trekanten har tre symmetriaks. I den likesidlige trekanten trekkes bisektoren fra toppunktet i en vinkel til motsatt side, og kutter den i midtpunktet. Du er i poeng som heter Incenter.
• MediaTrix: Det er et segment vinkelrett på siden av trekanten som har sin opprinnelse midt i dette. Det er tre formidlinger i en trekant, og de er enige på et punkt som kalles circumentro.
• Høyden: Det er linjen som går fra toppunktet til siden som er motsatt, og også denne linjen er vinkelrett på den siden. Alle trekanter har tre høyder som sammenfaller på et punkt som heter Ortotener.

I den følgende grafen observerer vi en Scalene Triangle der noen av de nevnte komponentene er detaljerte

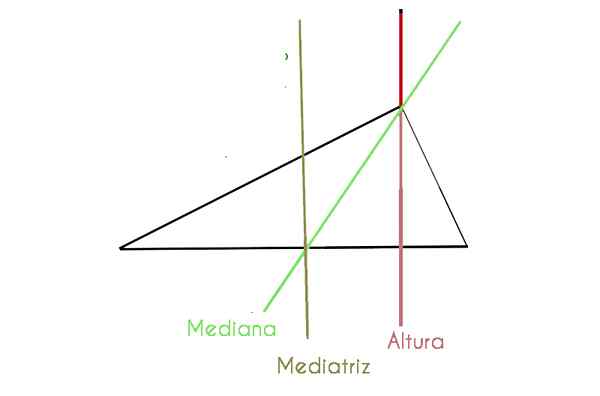Vi kan tydelig se komponentene, noe som er vanskeligere i den likesidelige trekanten, siden noen sammenfaller. Vi forklarer dem nedenfor:

Bisektoren, median og mediatrix er tilfeldig

Bisektoren deler seg ved siden av en trekant i to deler. I likeverdige trekanter vil den siden bli delt inn i to nøyaktig de samme delene, det vil si at trekanten vil bli delt inn i to kongruente rektangler trekanter.

Dermed sammenfaller bisektoren trukket fra en hvilken.

Kan tjene deg: proporsjonalitetsrelasjoner: konsept, eksempler og øvelser

Eksempel:

Følgende figur viser ABC -trekanten med en midt D som deler en av sidene i to AD- og BD -segmenter.

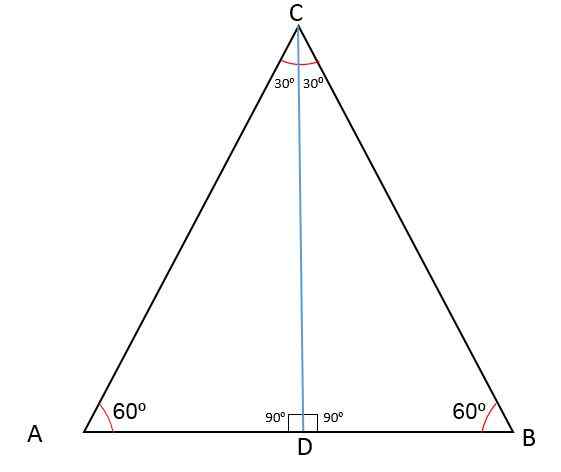
Når du tegner en linje fra punkt D til motsatt toppunkt, oppnås median CD per definisjon, som er relativt til toppunkt C og til siden AB.

Når CD -segmentet deler ABC -trekanten i to like CDB- og CDA -trekanter, betyr det at det vil være tilfelle av kongruens: side, vinkel, side og derfor vil CD også være BCD -bisektor.

Når du tegner CD -segmentet, er toppunktvinkelen delt i to like vinkler på 30^enten, Vinkelen på toppunktet A fortsetter å måle 60^enten Og CD -linjen danner en vinkel på 90^enten Angående midtpunktet d.

CD -segmentet danner vinkler som har samme mål for ADC- og BDC -trekanter, det vil si at de er supplerende på en slik måte at målet for hver vil være:

Med. (ADB) + Med. (ADC) = 180^enten

2 _* Med. (ADC) = 180^enten

Med. (ADC) = 180^enten ÷ 2

Med. (ADC) = 90^enten.

Og så er CD -segmentet også mediatrix på AB -siden.

Bisektoren og høyden er tilfeldig

Når bisektoren sporer fra toppunktet i en vinkel til midtpunktet på motsatt side, deler dette den likestående trekanten i to kongruente trekanter.

På en slik måte at det dannes en vinkel på 90^enten (rett). Dette indikerer at dette linjesegmentet er helt vinkelrett på den siden, og per definisjon at linjen vil være høyden.

På denne måten faller bisektoren til en hvilken.

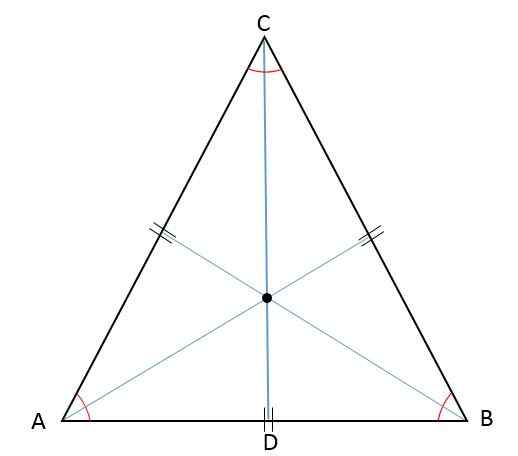
Orocentro, Baricentro, Incentro og Colecentro Coinsides

Som høyden er median, bisektor og mediatrix representert samtidig av det samme segmentet, i en liksidig trekant møtepunktene i disse segmentene -Ortosenteret, baricenter, incenter og omskjæring -vil bli funnet på samme punkt:

Egenskaper

Hovedegenskapen til de likestående trekantene er at de alltid vil være isosceles -trekanter, siden isoscelene er dannet av to kongruente sider og likevekt av tre.

På denne måten arvet de likeverdige trekantene alle egenskapene til Isosceles -trekanten:

Interne vinkler

Summen av interne vinkler er alltid lik 180^enten, Og siden alle dens vinkler er kongruente, så vil hver av disse måle 60^enten.

Eksterne vinkler

Summen av ytre vinkler vil alltid være lik 360^enten, Derfor vil hver ytre vinkel måle 120^enten. Det er fordi indre og ytre vinkler er supplerende, det vil si ved å legge dem til at de alltid vil være lik 180^enten.

Sum av sidene

Summen av tiltakene på to sider må alltid være større enn målet på tredje side, det vil si A + B> C, hvor A, B og C er målingene på hver side.

Kongruente sider

De liksidige trekantene har sine tre sider med samme mål eller lengde; det vil si at de er kongruente. Derfor må du i forrige element = b = c.

Kongruente vinkler

De likesidelige trekantene er også kjent som likeverdige trekanter, fordi deres tre indre vinkler er kongruente med hverandre. Dette er fordi alle sidene deres også har samme tiltak.

Det kan tjene deg: nominell variabel: konsept og eksempler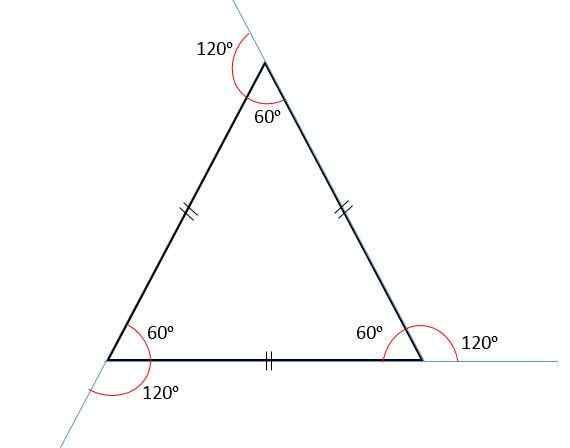

Hvordan beregne omkretsen?

Omkretsen til en polygon beregnes av summen av sidene. Som i dette tilfellet den likesidlige trekanten har alle sine sider med samme mål, beregnes omkretsen med følgende formel:

P = 3 _* side.

Hvordan beregne høyden?

Siden høyden er linjen vinkelrett på basen, deler den i to like deler ved å strekke seg til motsatt toppunkt. Dermed dannes to trekanter like rektangler.

Høyden (h) representerer den motsatte kateto (a), halvparten av vekselstrømsiden til den tilstøtende kateto (b) og BC -siden representerer hypotenusen (c).

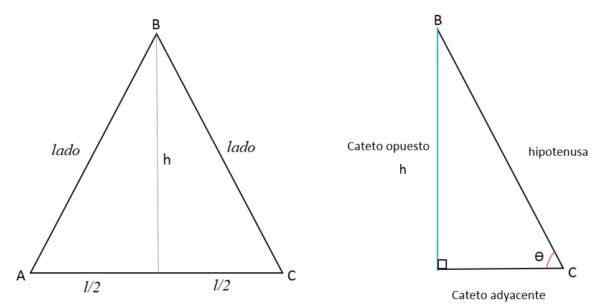
Ved hjelp av Pythagoras -teoremet kan verdien av høyden bestemmes:

til² + b² = c²

Hvor:

til² = høyde (h).

b² = side b / 2.

c² = side a.

Bytte ut disse verdiene i Pythagoras -teoremet, og rydde høyden du har:

h² + ( l / 2)² = l²

h² +  l²/ 4 = l²

h² = l²  -  l²/ 4

h² = (4_*l² -  l²) / 4

h² =  3_*l² /4

√h² = √ (3_*l² /4)

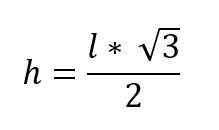
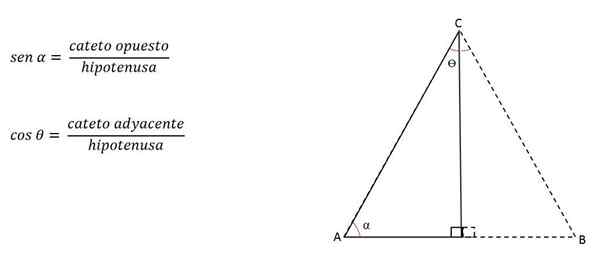
Hvis vinkelen dannet av kongruente sider, er høyden (representert av et ben) kjent, kan den beregnes ved å anvende de trigonometriske grunnene.

Kategoriene kalles motsatt eller tilstøtende avhengig av vinkelen som blir tatt som referanse.

For eksempel, i forrige figur vil kateto h være motsatt for vinkel C, men ved siden av vinkel B:

Dermed kan høyden beregnes med:

Hvordan beregne sidene?

Det er tilfeller der tiltakene på trekantesidene ikke er kjent, men høyden og vinklene som dannes i toppunktene.

For å bestemme området i disse tilfellene er det nødvendig å anvende trigonometriske grunner.

Å kjenne vinkelen til en av dens hjørner, er kategorien identifisert og den tilsvarende trigonometriske grunnen brukes:

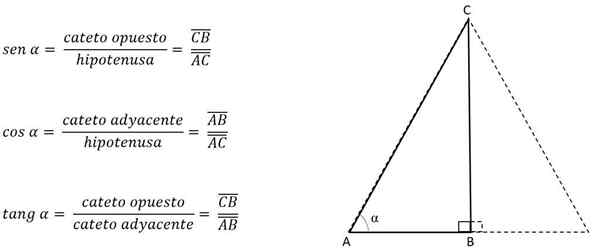
Dermed vil kateto ab være imot vinkel C, men ved siden av vinkelen a. Avhengig av siden eller benet som tilsvarer høyden, blir den andre siden ryddet for å oppnå verdien av dette, vel vitende om at de tre sidene alltid vil ha samme tiltak i en liksidig trekant vil ha samme mål.

Hvordan beregne området?

Trekantene beregnes alltid med samme formel, multipliserer basen etter høyde og deling med to:

Område = (B _* H) ÷ 2

Å vite at høyden er gitt av formelen:

Øvelser

- Første trening

Sidene av en ABC -likesidt trekant måler 20 cm hver. Beregn høyden og området til den polygonen.

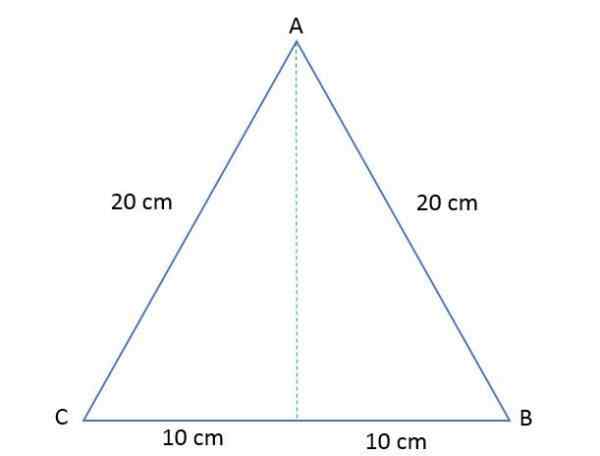
Løsning

For å bestemme området for den likesidelige trekanten er det nødvendig å beregne høyden, vel vitende om at når den tegner den, deler den trekanten i to like rektangler.

På den måten kan du bruke Pythagoras teorem for å finne det:

til² + b² = c²

Hvor:

A = 20/2 = 10 cm.

B = høyde.

C = 20 cm.

Dataene erstattes i teoremet:

10² + b² = 20²

100 cm + b² = 400 cm

b² = (400 - 100) cm

b² = 300 cm

B = √300 cm

B = 17,32 cm.

Det vil si at høyden på trekanten er lik 17,32 cm. Nå er det mulig å beregne det gitte trekantområdet ved å erstatte formelen:

Område = (B _* H) ÷ 2

Område = (20 cm _* 17,32 cm) ÷ 2

Det kan tjene deg: lineære transformasjoner: egenskaper, hva er bruk, typer, eksempler

Område = 346,40 cm² ÷ 2

Område = 173,20 cm².

En annen enklere måte å løse øvelsen på er å erstatte dataene i den direkte formelen i området, der verdien av høyden også implisitt er funnet:

- Andre trening

I et felt som har formen som en likestående trekant, vil blomster plante. Hvis omkretsen av det terrenget lik 450 m, beregner antall meter som okkuperte blomstene.

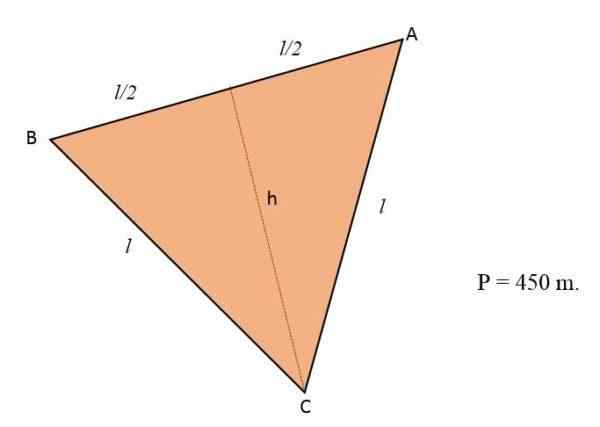
Løsning

Når vi vet at omkretsen av en trekant tilsvarer summen av de tre sider, og ettersom terrenget er formet som en liksidig trekant, vil de tre sidene av dette ha samme mål eller lengde:

P = side + side + side = 3 _* l

3 _* l = 450 m.

L = 450 moh ÷ 3

L = 150 m.

Nå er det bare nødvendig å beregne høyden på den trekanten.

Høyden deler trekanten i to kongruente rektangler trekanter, der en av kategoriene representerer høyden og den andre halvparten av basen. Ved Pythagoras -teoremet kan høyden bestemmes:

til² + b² = c²

Hvor:

til = 150 m ÷ 2 = 75 m.

c = 150 m.

b = høyde

Dataene erstattes i teoremet:

(75 m)² + b² = (150 m)²

5.625 m + b² = 22.500 m

b² = 22.500 m - 5.625 m

b² = 16.875 m

b = √16.875 m

b = 129,90 m.

Dermed vil området som blomster vil okkupere være:

Område = b * h ÷ 2

Område = (150 m _* 129,9 m) ÷ 2

Område = (19.485 m²) ÷ 2

Område = 9.742,5 moh²

- Tredje øvelse

ABC -likestående trekant er delt av et linjesegment som går fra toppunktet C til midtpunktet D, som ligger på motsatt side (AB). Dette segmentet måler 62 meter. Beregn området og omkretsen til den liksidige trekanten.

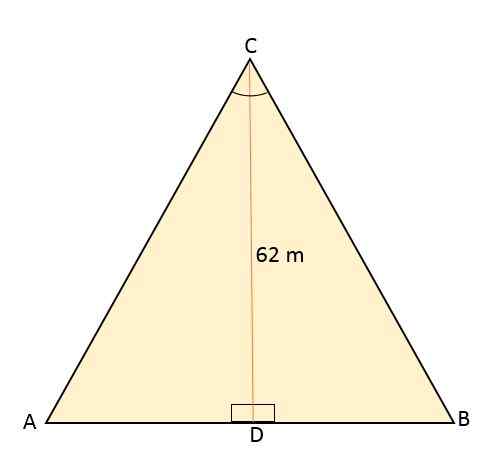
Løsning

Når vi vet at den likesidlige trekanten er delt av et linjesegment som tilsvarer høyden, og dermed danner to kongruente rektangler, deler dette også vinkelen på toppunktet C i to vinkler med samme mål, 30^enten Hver.

Høyden danner en vinkel på 90^enten Med hensyn til segment AB, og toppunktets vinkel for å måle 60^enten.

Deretter ved å bruke vinkelen på 30 som referanse^enten, CD -høyde er etablert som en kateto ved siden av vinkelen og BC som hypotenusa.

Fra disse dataene kan verdien av en av sidene av trekanten bestemmes ved å bruke de trigonometriske grunnene:

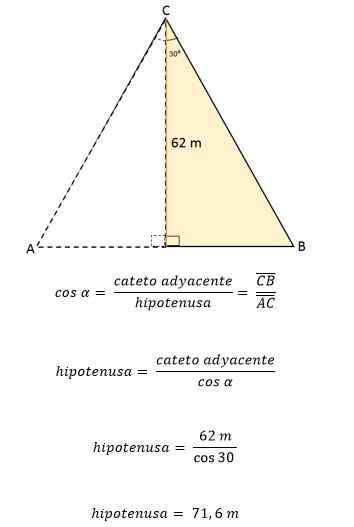
Som i den likesidelige trekanten har alle sider nøyaktig samme mål eller lengde, betyr det at hver side av ABC -likestilt trekant er lik 71,6 meter. Å vite det, er det mulig å bestemme ditt område:

Område = b * h ÷ 2

Område = (71,6 m _* 62 m) ÷ 2

Område = 4.438,6 m² ÷ 2

Område = 2.219,3 m²

Omkretsen er gitt av summen av sine tre sider:

P = side + side + side = 3 _* l

P = 3_*l

P = 3 _* 71,6 m

P = 214,8 m.

Referanser

1. Álvaro Rendón, til. R. (2004). Teknisk tegning: Aktivitetsnotatbok.
2. Arthur Goodman, L. H. ( nitten nittiseks). Algebra og trigonometri med analytisk geometri. Pearson Education.
3. Baldor, a. (1941). Algebra. Havana: kultur.
4. Barbosa, J. L. (2006). Flat euklidisk geometri. SBM. Rio de Janeiro, .
5. Coxford, a. (1971). Geometri En transformasjonsmetode. USA: Laidlaw Brothers.
6. Euclid, r. P. (1886). Euclids elementer av geometri.
7. Héctor Trejo, J. S. (2006). Geometri og trigonometri.
8. León Fernández, G. S. (2007). Integrert geometri. Metropolitan Technological Institute.
9. Sullivan, J. (2006). Algebra og trigonometri. Pearson Education.