Typer funksjoner og grafene deres

Det er mangfoldig Typer funksjoner som brukes til å modellere problemer i grener av kunnskap som naturvitenskap, administrasjon, økonomi og samfunnsvitenskap. Matematisk sett er en funksjon et forhold mellom to eller flere variabler.

Mange ganger er visse gjenstander eller mengder relatert til hverandre. Disse beløpene er representert med variabler. For eksempel er det to relaterte variabler, som tilhører to sett A og B, ikke nødvendigvis numeriske, selv om de meste av tiden er-.

For å bli betraktet som en funksjon, må dette forholdet oppfylle to forhold: det første er at alle elementene i startsettet til å delta, og det andre, at hvert element i nevnte sett er relatert til bare ett av elementene i sett B.

Variabler kalles vanligvis med bokstaver x og og, med x som uavhengig variabel og og som avhengig variabel. Naturligvis kan de kalles på hvilken som helst annen måte, og velge navnet på variabelen i samsvar med størrelsen den representerer.

Forholdet mellom de to er betegnet gjennom brevet F -eller en annen bokstav i alfabetet-og er representert på flere måter, for eksempel et sett med bestilte par, en graf, et verbalt uttrykk eller en algebraisk formel:

• f (x) = x + 1
• Befolkning P av en viss by i en viss tidsintervall t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Funksjoner er preget av å ha domene og rekkevidde eller rute. Domene er settet med verdier som variabelen x Du kan ta, mens rekkevidden er settet med verdier som skaffer seg den avhengige funksjonen eller variabelen og.

Klassifisering av funksjoner

Funksjonene kan grupperes i 5 store kategorier, noe som gjenspeiles i følgende ordning, der hver gruppe er merket med et romertall og en farge. Fra venstre mot høyre er funksjonene klassifisert i henhold til:

• I) dens form.
• Ii) Symmetri.
• Iii) Måten å uttrykke variabelen.
• Iv) dens kontinuitet og monotoni.
• V) Måten domeneelementene er relatert til rekkevidden.

Hovedklassifiseringskriterier for funksjoner. Kilde: f. Zapata.

Følg nå en kort beskrivelse av hver av de typer funksjoner med sine respektive eksempler.

I) funksjoner i henhold til dens form

Yo.1) Algebraiske funksjoner

De er blant de mest brukte funksjonene i mange vitenskapsfelt, og derfor er de de mest kjente. De er preget av å ha som korrespondanseregel, et algebraisk uttrykk.

På sin side blir algebraiske funksjoner delt inn i følgende typer:

• Yo.1.a) Polynom eller polynom.
• Yo.1.b) rasjonell.
• Yo.1.c) irrasjonell.
• Yo.1.d) etter seksjoner.

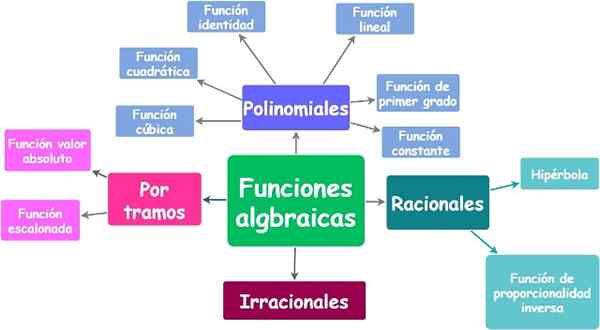Algebraiske funksjoner og deres typer. Kilde: f. Zapata.

Yo.1.a) Polynom- eller polynomfunksjoner

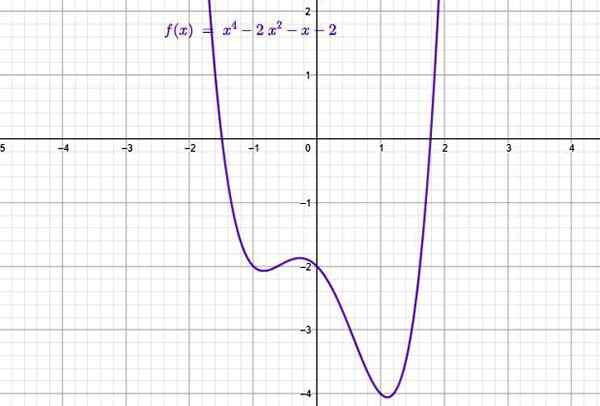Eksempel på funksjon av polynomtype. Kilde: f. Zapata gjennom Geogebra.

De består av summer av vilkår hvis generelle form er:

P (x) = a_nxⁿ + til _N-1x^N-1 +… til₁x + a₀

Hvor koeffisientene til_n, til _N-1… til₁, til₀ De er reelle tall og n er et heltall. Domenet til polynomfunksjoner er settet R for reelle tall og er også kontinuerlige funksjoner gjennom dette domenet.

I den øvre figuren er grafen for følgende polynomfunksjon av rekkefølge 4:

f (x) = x⁴ - 2x² - x -2

Blant polynomfunksjonene skilles noen spesielle tilfeller, i henhold til verdiene til koeffisientene. Det er verdt å vurdere nøye, fordi de er veldig nyttige i flere situasjoner:

i) Konstant funksjon

Det er en konstant funksjon når alle koeffisienter blir kansellert, bortsett fra₀:

f (x) = a₀ = k

Grafen til den konstante funksjonen er en rett linje parallell med den horisontale aksen, for eksempel linjer:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

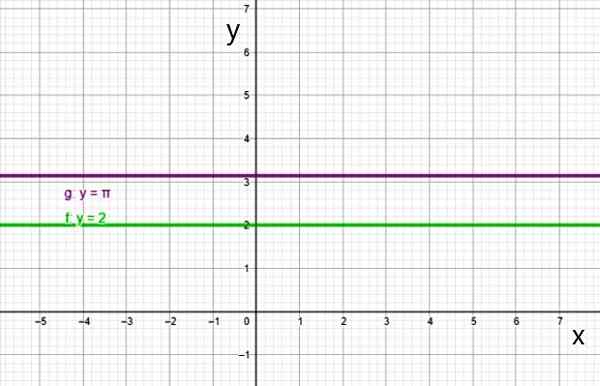To eksempler på konstant funksjon. Kilde: f. Zapata.

Ii) Første gradsfunksjon

Den første -graderingsfunksjonen eller relaterte funksjonen er at hvis graf er en rett linje. Det er et spesielt tilfelle av polynomfunksjonen der alle annulleringskoeffisientene₁ allerede₀. Det er gitt av:

f (x) = a₁x + a₀

Verdien a₁ Det er skråningen på linjen, som gir et mål på sin tilbøyelighet, og₀ Det er kuttet på linjen med den vertikale aksen. Begge kan ta positive eller negative verdier.

Eksempler på første gradsfunksjon er følgende:

• G (x) = 2x -1
• H (x) = -6x +5/2

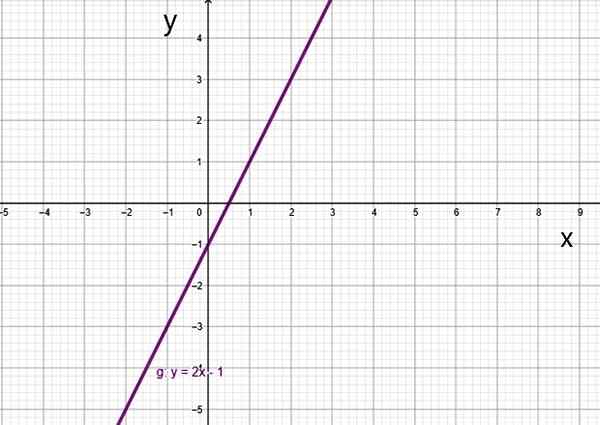Første gradsfunksjon f (x) = 2x-1. Kilde: f. Zapata.

Det er en spesiell sak, som er den lineære funksjonen.

Kan tjene deg: Sentral tendensmål for grupperte data: Formler, øvelser

iii) Lineær funksjon

Når koeffisienten til₀ Det er 0, funksjonen går alltid gjennom opprinnelsen og uttrykkes med f (x) = a₁X, ringer Lineal FUNTION, hvordan har du det:

• f (x) = 5x
• G (x) = -7x

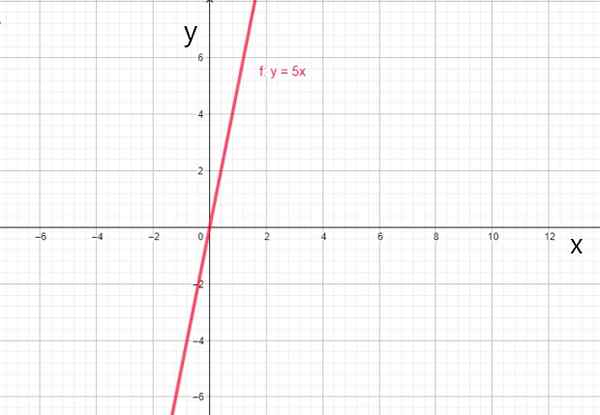Lineær funksjon f (x) = 5x. Kilde: f. Zapata.

iv) Identitetsfunksjon

Det er et spesielt tilfelle av den lineære funksjonen, der₁ = 1:

f (x) = x

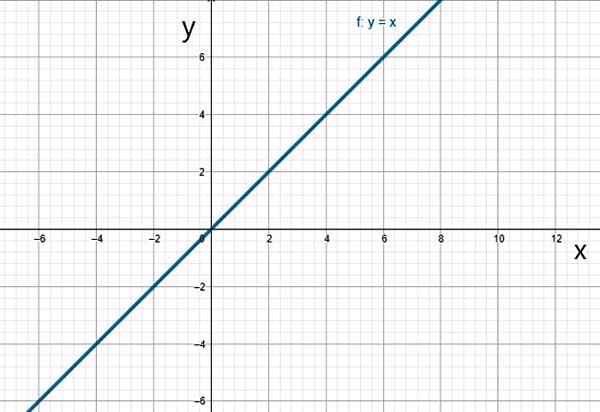Identitetsfunksjonen. Kilde: f. Zapata.

v) Kvadratisk funksjon

Den har den generelle formen:

f (x) = a₂x² +til₁x + a₀

Med en₂  ≠ 0.

Grafen er en lignelse hvis aksiale eller symmetri -aksen er parallell med ordinens akse. Krysser alltid den vertikale aksen ved koordinatpunktet x = 0, y = a₀. Når det gjelder kryss med den horisontale aksen, kan den ha opptil maksimalt 2.

Eksempler på kvadratiske funksjoner er:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

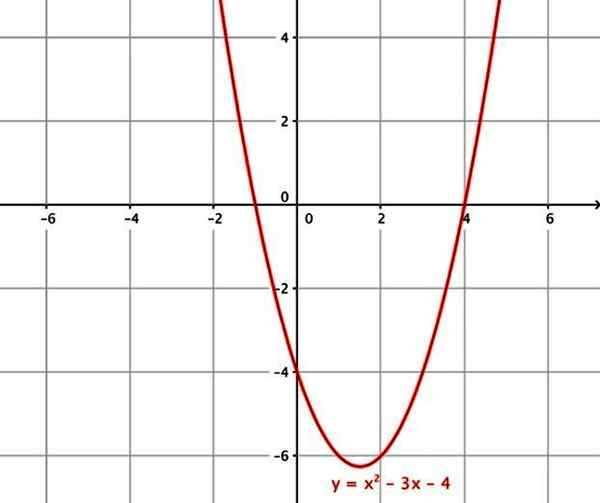Den kvadratiske funksjonen. Kilde: Wikimedia Commons.

vi) kubisk funksjon

Som navnet tilsier, inneholder den kubiske funksjonen en kraft på 3:

f (x) = a₃x³ + til₂x² + til₁x + a₀

Koeffisienten a₃ Det er alltid forskjellig fra 0, som i disse tilfellene:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

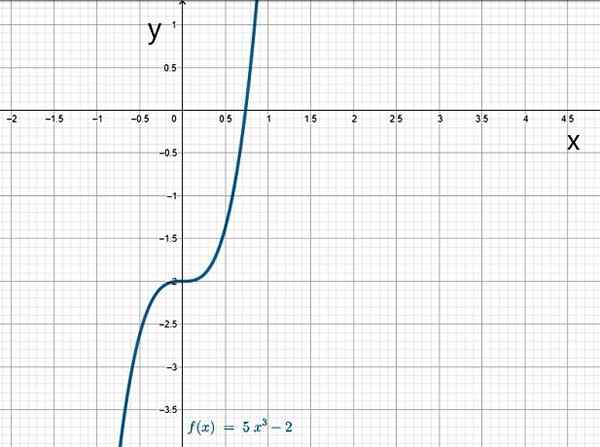Kubisk funksjon. Kilde: f. Zapata.

Yo.1.b) Rasjonelle funksjoner

Rasjonelle funksjoner har skjemaet:

 Hvor P (x) og Q (x) er irreducible polynomer, det vil si at de ikke har noen felles faktor og i alle fall q (x) ≠ 0.

Fra domenet til rasjonelle funksjoner, alle verdiene som annullerer nevner Q (x), det vil si dets røtter, mens verdiene på verdiene til verdiene til og som bestemmer de horisontale asymptotene.

En asymptot er en linje som funksjonen nærmer seg, både til venstre og til høyre, over eller under, men aldri krysser. Slike linjer kan være vertikale, horisontale eller tilbøyelige.

Eksempler på rasjonelle funksjoner er:

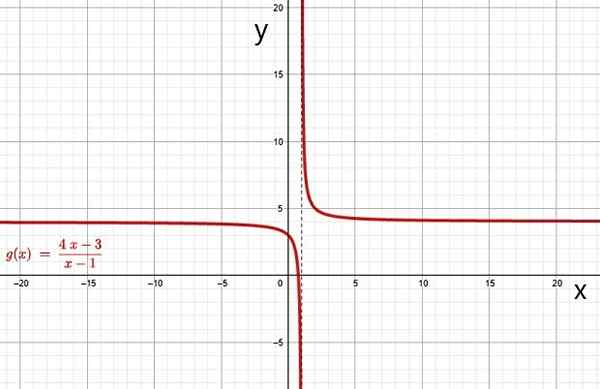
Rasjonell funksjon. Kilde: f. Zapata gjennom Geogebra.

i) Hyperbola

Grafen til en rasjonell funksjon er en hyperbola når polynom i nevner Q (x) har grad 1. Grafen til funksjonene f (x) og g (x) av eksemplene ovenfor er hyperbolas, den kan enkelt sjekkes gjennom en gratis online grafikkprogramvare, for eksempel Geogebra.

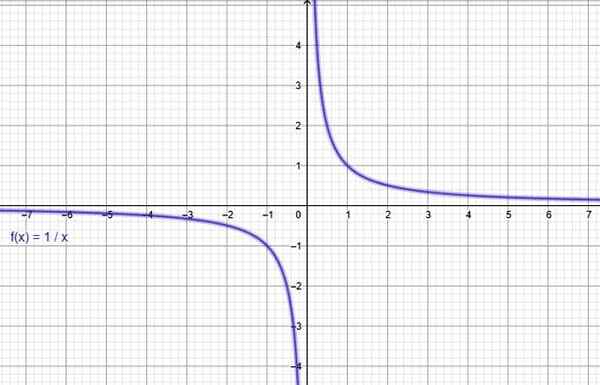Funksjonen y = 1/x. Kilde: f. Zapata gjennom Geogebra.

Ii) omvendt proporsjonalitetsfunksjon

Det er en funksjon av form:

Der C er et reelt tall forskjellig fra 0. Domenet er settet med reelle tall bortsett fra 0.

Yo.1.c) Irrasjonelle funksjoner

Er de hvis uavhengige variabel er under et radikalt tegn. Dens generelle form er:

Noen av disse funksjonene kan være:

• 
• 

Domenet til disse funksjonene bestemmes som følger:

-Hvis røttene er av dreiemomentindeks, må den subradiske mengden f (x) alltid være 0 eller positiv.

-Når røttene er rare, kan f (x) være positive eller negative. Derfor er funksjonen til funksjonen i dette tilfellet de virkelige tallene.

For eksempel domenet til:

Det er settet med reelle tall slik at X-3 er større enn eller lik 0. I dette tilfellet må x være større enn eller lik 3. Derfor er domenet til denne funksjonen settet med verdiene for intervallet [3, ∞+).

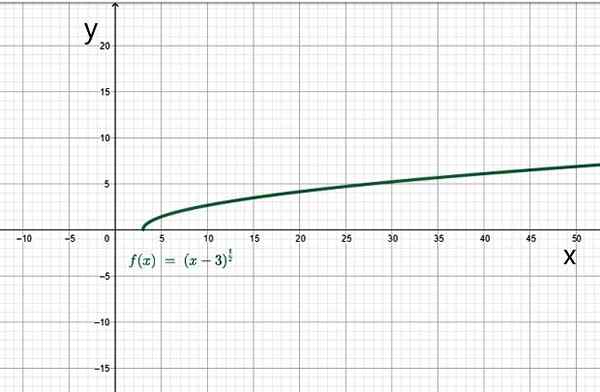 Eksempel på irrasjonell funksjon. Kilde: f. Zapata.

Yo.1.d) funksjoner i stykker eller av seksjoner

Funksjonen i deler, etter seksjoner eller stykker er en som krever mer enn en formel for forskjellige domeneverdier. Her er noen eksempler på søknaden din:

-Priser for å sende pakker per post, avhengig av vekt eller volum, opprinnelse og destinasjon for det samme.

-Priser for tjenester, for eksempel telefoni og strøm.

-Salg av billetter til museer eller fornøyelsesparker, avhengig av alder.

I matematisk form kan en funksjon i deler være, for eksempel:

Domenet til en funksjon i deler avhenger av dens definisjon. I forrige eksempel er domenet settet dannet av: (-∞, -1) ∪ [1,+∞).

Den absolutte verdifunksjonen. Kilde: f. Zapata gjennom Geogebra.

Ii) Escalonada -funksjon

Grafen til denne funksjonen etter seksjoner består av trinn, for eksempel en stige eller kan være av forskjellige høyder, avhengig av hvordan funksjonen er definert.

Det kan tjene deg: Hipparco of Nicea: Biografi og bidrag til vitenskap

For dette er det valgt et begrenset intervall [a, b] som inneholder et visst begrenset antall diskontinuiteter, kalt x_Yo < x₁ < x₂ <… . x_n  Og et åpent intervall er valgt (x_Yo , x_i+1) For å gi den en konstant av verdi s_Yo, Med hoppene på punktene x_Yo. Verdien av S_Yo Det er høyden på det aktuelle trinnet.

Et eksempel på en forskjøvet funksjon er hele delen, som tar et hvilket. Følgende er en hel del:

[x] = (større heltall ≤ x)

I følge denne funksjonen er hele delen av 2.5 er:

[2.5] = (større heltall ≤ 2.5) = 2

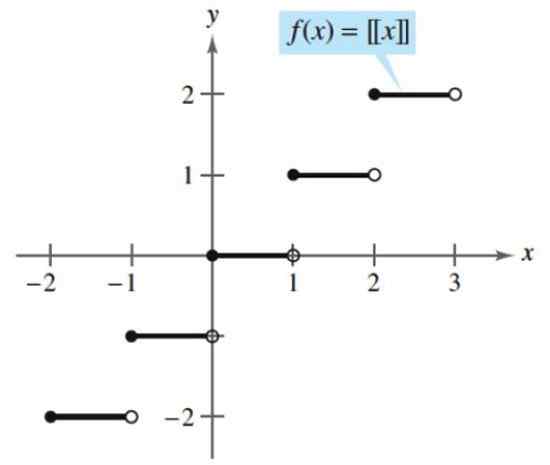Hele delen av. Kilde: Larson, R. Beregning med analytisk geometri. McGraw-Hill.

Yo.2) Transcendente funksjoner

Ikke -algebraiske funksjoner kalles transcendent. Eksponentielle, logaritmiske og trigonometriske funksjoner er transcendente funksjoner.

I dem variabelen x Det er en del av argumentet for funksjonen eller som en del av eksponenten eller indeksen for noen rot, for eksempel:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Transcendente funksjoner har mange applikasjoner, for eksempel i studiet av vibrasjoner og bølger, sannsynlighetsfordelinger, modellering av bølgene, veksten av forskjellige populasjoner, radioaktivt forfall, renter og mange flere. 

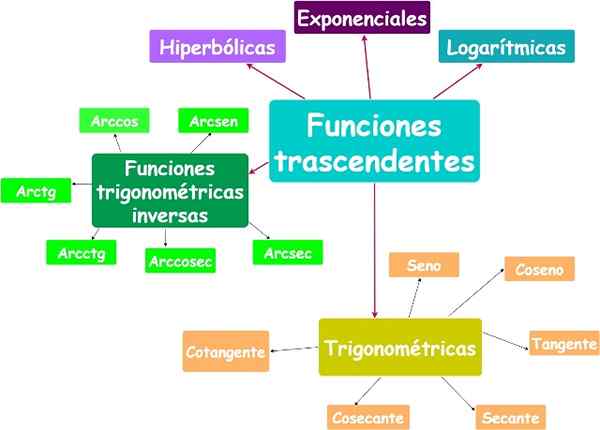Hovedtranscendente funksjoner. Kilde: f. Zapata.

Yo.2.a) Eksponentiell funksjon 

Den eksponentielle funksjonen er definert av:

f (x) = a^x

Hvor A er basen, som alltid er et positivt antall 1, og variabelen, et reelt tall, vises i eksponenten. Generelt er den eksponentielle funksjonen skrevet:

f (x) = a⋅a^Bx

Her er a og b reelle koeffisienter. Følgende er funksjoner av denne typen:

• f (x) = 5e^x
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

Utgangspunkt og, hvor og Det er antall Euler 2.71828 ..., vises ofte i problemer med vitenskap og ingeniørfag, samt statistikk. Når funksjonen har denne basen kalles Naturlig eksponentiell funksjon.

Domenet til den eksponentielle funksjonen er settet med reelle tall, mens rekkevidden er de positive tallene.

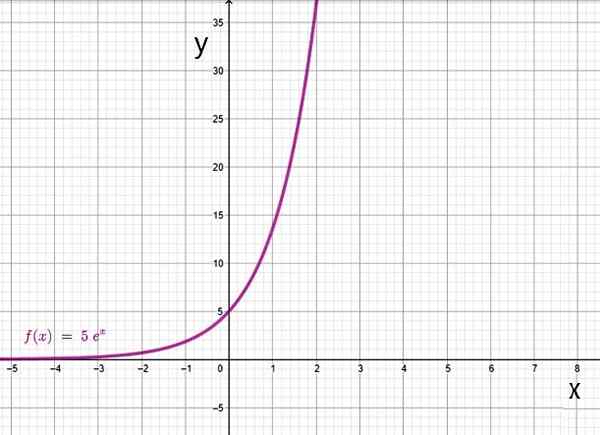Eksponentiell funksjon basert på. Kilde: f. Zapata gjennom Geogebra.

Yo.2.b) logaritmefunksjon

For sin del er logaritmefunksjonen basert på til Det er den inverse funksjonen til eksponentiell funksjon basert på til. Ja:

Logg_til x = y

Så:

x = a^og

Spesielt, hvis basen til logaritmen er nummer E, kalles funksjonen Neperian logaritmefunksjon Og det er betegnet som ln. Funksjoner av denne typen er:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Domenet til logaritmefunksjonen, uavhengig av basen, er de positive reelle tallene, ikke inkludert 0. Det vil si at det ikke er noen logaritmer av negative tall eller 0.

Imidlertid kan en logaritme være 0 eller negativ: logaritmen til antallet mellom 0 og 1 er negativ og oppnår for sin del_til 1 = 0.

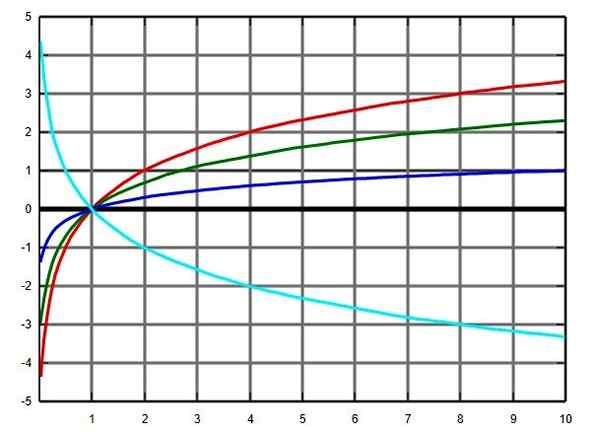Logaritmefunksjonsgraf i flere baser: base 2 i rød, grønn E, blå -base og turkis på base 0.5. Kilde: Wikimedia Commons.

Yo.2.c) Trigonometriske funksjoner

De er de som kommer fra de trigonometriske grunnene: bihule, kosinus, tangent, tørking, harmonering og cotangent av en vinkel x. De er betegnet som henholdsvis:

Sen X, Cos X, Tg X, Sec X, Harm X og Cotg X

De er periodiske funksjoner, noe som betyr at den.

Eksempler på trigonometriske funksjoner er:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Variabel X er uttrykt i radianer.

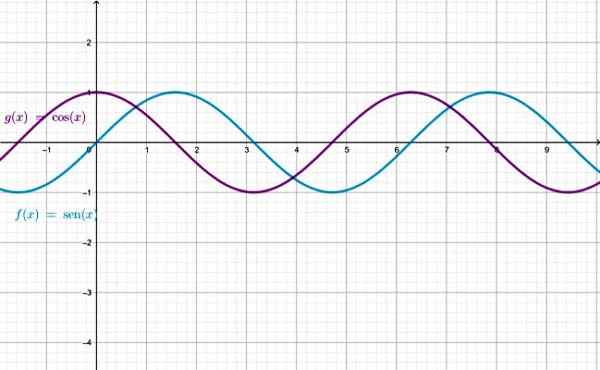Graf over funksjonene Sen X og Cos X, merk at de er identiske, bortsett fra at den ene er fortrengt med hensyn til den andre. Kilde: f. Zapata gjennom Geogebra.

Mestring av Sen X- og Cos X -funksjonene er settet med reelle tall. For de gjenværende funksjonene er det X -verdier som funksjonen ikke er definert for:

-Tg x -funksjonen eksisterer ikke når x = ± π /2, ± 5π /2 ... dette er, alle de rare multiplene av π /2.

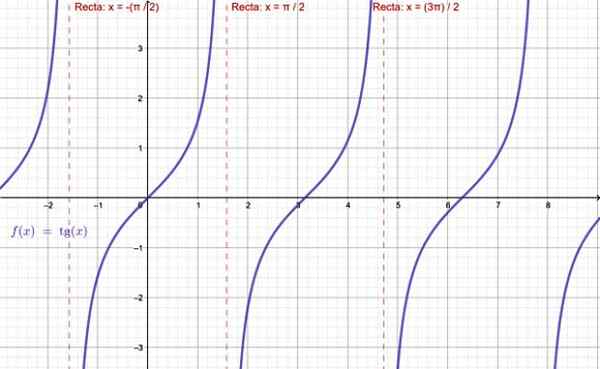Grafering av tangensfunksjonen. Kilde: f. Zapata gjennom Geogebra.

-Når det gjelder f (x) = cotg x, er denne funksjonen ikke definert for hele multiplene på π: ± π, ± 2π, ± 3π ..

Kan tjene deg: Law of Signs

-Y = sec x -funksjonen er ikke gyldig når cos x = 0, som ekskluderer x = ± π /2, ± 5π /2 ... av dets domene.

-Til slutt, for f (x) = skade x, hører ikke hele multiplene av π til deres domene.

Yo.2.d) Hyperbolske funksjoner

Hyperbolske funksjoner er spesielle kombinasjoner av eksponentielle og^x og e^-x Og de blir kalt som en barm, Coseno .. .hyperbolsk. Som med trigonometriske funksjoner, også kalt "sirkulær", er det 6 hyperbolske funksjoner:

-Hyperbolsk bihule Senh x:

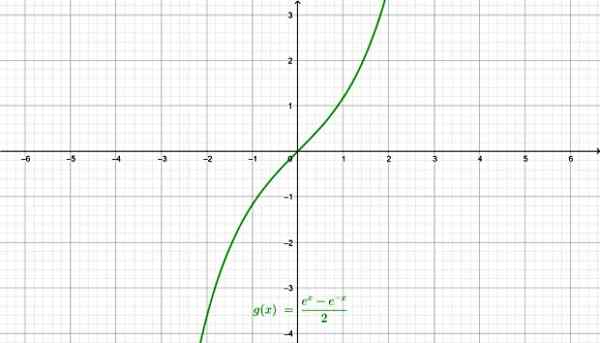Den hyperbolske bihulefunksjonen. Kilde: f. Zapata gjennom Geogebra.

-Hyperbolsk kosinus Cosh x:

 -Hyperbolsk tangent tanh x:

 -Hyperbolsk høst CSCH X:

 -Hyperbolsk secant Sech x:

-Hyperbolsk kotangent Coth x:

En fleksibel kabel, laget av ensartet og hengemateriale mellom to punkter, tar form av en kurve som kalles Katenær, som uttrykkes som en hyperbolsk kosinus:

Yo.2.e) Inverse trigonometriske funksjoner

De tilsvarer det inverse av trigonometriske funksjoner. For eksempel hva som vil være vinkelen (bue) hvis bryst er verdt 0.5?

Svaret er arc sen 0.5, som lyder “Arc Sinus of 0.5 ”, og denne vinkelen er 30º, selv om det i prinsippet ikke ville være den eneste vinkelen hvis barm er verdt 0.5, siden Sen X -funksjonen er periodisk. Det som skjer er at hvis Sen X -funksjonen tas gjennom hele sitt domene, ville den ikke ha omvendt, så Arcoseno -funksjonen ikke kunne defineres. Problemet blir avgjort ved å begrense alt til vinklene mellom -π/2 og +π/2.

Dette kan uttrykkes som følger:

Hvis buen sen x = θ, betyr det at sin θ = x

Med -π/2 ≤ θ ≤ π/2.

En annen notasjon brukt for bue sen x er f (x) = sin^-1 x. Grafen er vist nedenfor:

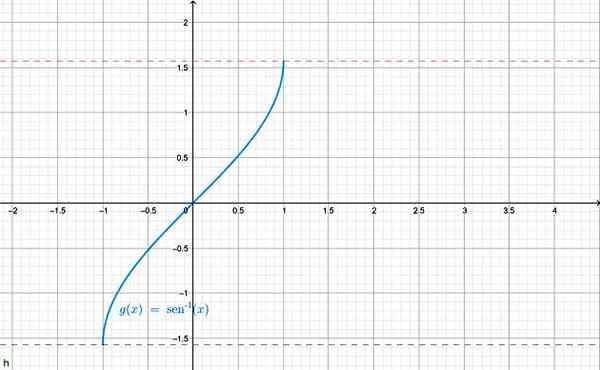Arcsen x funksjonsgrafikk. Kilde: f. Zapata gjennom Geogebra.

Det er også mulig å definere omvendt for de andre trigonometriske funksjonene, for eksempel: bue cos x = θ og dermed. For hver og en er rangering riktig begrenset, for å være den omvendte av den tilsvarende trigonometriske funksjonen.

Ii) funksjoner i henhold til symmetrien

Ii.1) Par

Hvis det for alle x som tilhører domenet til f (x), blir det oppfylt at:

f (x) = f (-x)

Det sies at funksjonen er jevn, som de som følger:

• f (x) = x² - 3
• g (x) = cos x
• 

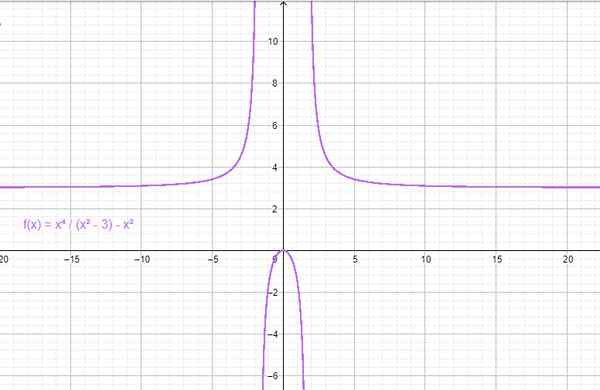  Eksempel på en parfunksjon. Kilde: f. Zapata gjennom Geogebra.

For eksempel å gjøre x = 1 i f (x) = x² - 3 er oppnådd:

f (1) = 1² - 3 = -2.

Og hvis x = -1, da:

f (-1) = (-1)² - 3 = -2.

Begge resultatene er identiske.

De jevne funksjonene har symmetri rundt den vertikale aksen, som det kan sees i forrige figur.

Ii.2) Odd funksjon

På den annen side, ja:

f (-x) = -f (x)

Funksjonen er merkelig.

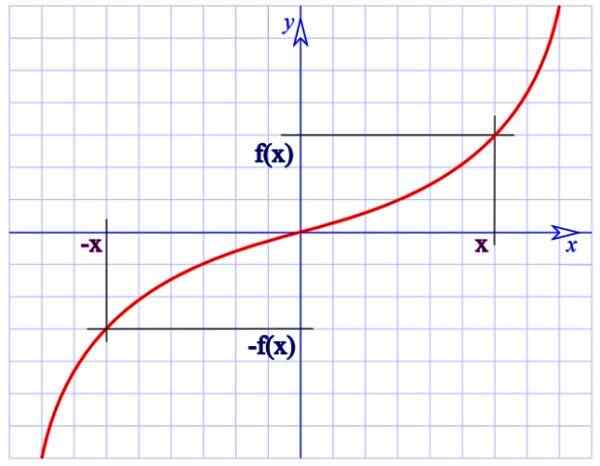En merkelig funksjon. Kilde: Wikimedia Commons.

For eksempel er funksjonen f (x) = 1/x i den øvre figuren merkelig, siden:

f (-x) = -1/x

OG

-f (x) = -1/x

En annen viktig imparfunksjon er f (x) = sin x.

Merk at rare funksjoner har 180º rotasjonssymmetri rundt opprinnelsen (grafen endres ikke hvis hvert punkt i den blir fylt 180º med hensyn til koordinatens opprinnelse).

Iii) funksjon i henhold til uttrykk for variabelen

Iii.1) eksplisitte funksjoner

De kommer til uttrykk direkte når det gjelder den avhengige variabelen som y = f (x). For eksempel:

• f (x) = x³

Iii.2) Implisitte funksjoner

I implisitte funksjoner virker ingen av variablene klare. De uttrykkes som f (x, y) = 0, for eksempel:

• x² + og² -3xy = 0
• xy = - x²+ X-5

Funksjonene som er beskrevet i hele denne artikkelen er eksplisitte funksjoner.

Iv) funksjoner i henhold til grafikken din

I henhold til grafen deres kan funksjonene være kontinuerlige eller diskontinuerlige. Kontinuerlige funksjoner kan spores uten å avbryte hjerneslaget, derimot, diskontinuerlige funksjoner er hopp. I følgende bilde er funksjonen diskontinuerlig ved x = a:

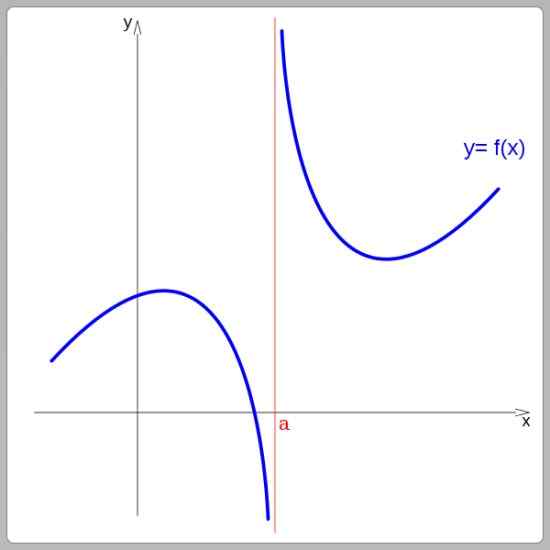Diskontinuitetsfunksjon ved x = a. Kilde: Wikimedia Commons.

Eksempler på kontinuerlige funksjoner er lineær funksjon, kvadratisk funksjon og sinus- og kosinusfunksjoner. Og blant diskontinuerlige funksjoner er den forskjøvede funksjonen og tangensfunksjonen.

V) fungerer i henhold til forholdet mellom elementene i domenet og rekkevidden

V.1) Injeksjonsfunksjon

En funksjon er Injeksjon Når det ikke er to forskjellige elementer i start- eller domenesettet, som har samme bilde i ankomstsettet.

Anta at virkelige funksjoner har, med mindre annet har spesifisert, for eksempel:

f (x) = 5x -2

All X -verdi som tilhører domenet til F (x), som er settet ℛ for de virkelige tallene, har et unikt, også ekte bilde. På den annen side, i denne andre funksjonen:

g (x) = x²

Det er forskjellige elementer i domenet som har samme bilde, for eksempel x₁= 2 og x₂= -2:

G (2) = g (-2) = 4.

Måten å identifisere en injeksjonsfunksjon fra grafen er å tegne en horisontal linje, hvis den kuttes til kurven på mer enn ett punkt, er funksjonen ikke -injektive.

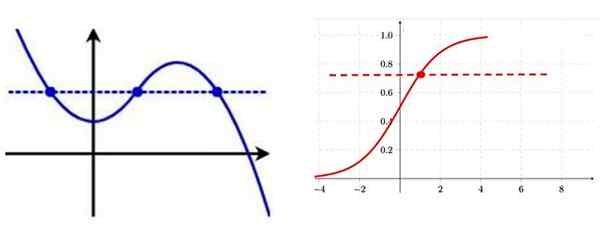Til venstre en FNs injeksjonsfunksjon, merk at det er flere punkter i grafen med samme vertikale koordinat. Til høyre har en injeksjonsfunksjon, på hvert av kurvenes punkter. Kilde: f. Zapata.

V.2) Overjektive funksjon

I Onjektive funksjoner, Alle elementer i ankomstsettet er et bilde av et element i startsettet. Et eksempel på oversvektiv funksjon er den samme f (x) = 5x -2, men g (x) = x² Det er det ikke, siden verdiene tatt g (x) bare er de positive virkelige og 0.

Imidlertid kunne domenet omdefineres slik at g (x) var overvektivt, hvis det for eksempel endres til alle positive virkelige pluss 0. 

V.3) Bijektive funksjon

Endelig kalles en funksjon som er både injeksjon og oversvivende Bijektiv. Eksempler på bijektive funksjoner er: den relaterte funksjonen, eksponentiell funksjon og logaritmefunksjonen.

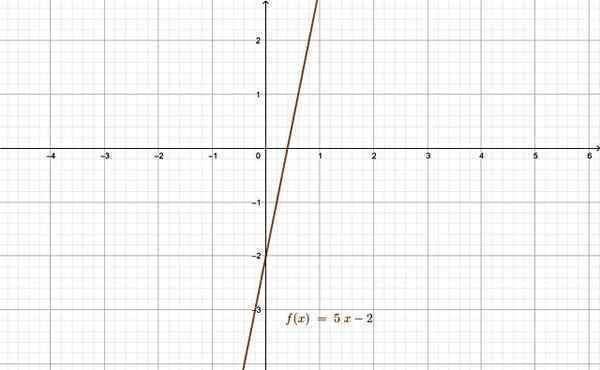Den relaterte funksjonen er et godt eksempel på bijjektivfunksjon. Kilde: f. Zapata gjennom Geogebra.

Referanser

1. E-Math Zone. Typer funksjoner. Gjenopprettet fra: Emathzone.com.
2. Hoffman, J.G. Valg av matematikkproblemer. Ed. Spphinx.
3. Matematikk er morsomt. Commons fungerer referanse. Gjenopprettet fra: Mathisfun.com.
4. Requena, b. Universformler. Typer funksjoner. Gjenopprettet fra: Universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.