Horisontale skytefunksjoner, formler og ligninger, øvelser

Han Horisontal skyting Det er lanseringen av et prosjektil med horisontal hastighet fra en viss høyde og overlatt til tyngdekraften. Uten å ta hensyn til luftmotstanden, vil banen beskrevet av mobilen ha form av en parabolabue.

Å projisere objekter horisontalt er ganske vanlig. Prosjektilene blir kastet med alle slags ender: fra steinene som demningene ble nedslått i begynnelsen av historien, til de som blir utført i ballsport og blir fulgt nøye med folkemengder.

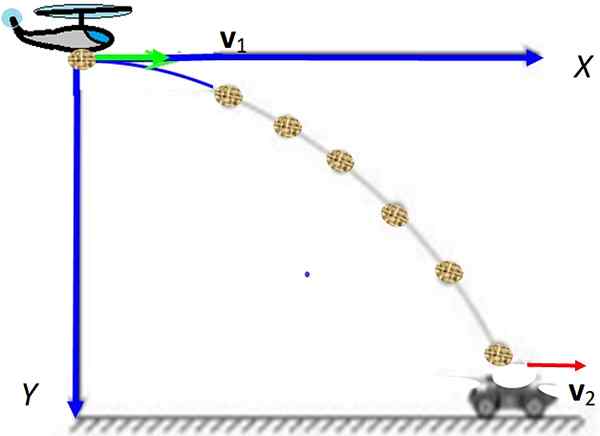
Figur 1. Horisontal skyting med røde hastighetskomponenter. Merk at den horisontale komponenten forblir konstant mens vertikal vokser. Kilde: Wikimedia Commons.

[TOC]

Kjennetegn

Hovedegenskapene ved den horisontale skytingen er:

-Den første hastigheten som er gitt til prosjektilet er vinkelrett på tyngdekraften.

-Bevegelsen foregår i et fly, så det er nødvendig med to koordinater: x og og.

-Det gjøres fra en viss høyde H over bakkenivå.

-Tiden som prosjektilet varer i luften kalles Flytid.

-Faktorer som luftmotstand eller svingninger tas ikke med i verdien av g.

-Formen, størrelsen og massen til prosjektilet påvirker ikke bevegelsen.

-Bevegelsen dekomponerer i to samtidige bevegelser: en vertikal ned under handlingen av g; Den andre, horisontale, med konstant hastighet.

Formler og ligninger

Kinematiske ligninger for horisontal lansering oppnås fra ligningene for fritt fall og de av den ensartede rettlinjede bevegelsen.

Kan tjene deg: intern energi

Som animasjon tydelig viser i figur 1, er prosjektilet utstyrt med en horisontal starthastighet, betegnet som v_enten = v_okse Yo (Det fet skrift i trykt tekst indikerer at det er en vektor).

Det bemerkes at den opprinnelige hastigheten har størrelsesorden v_okse og er rettet langs aksen x, Hva er retningen på enhetsvektoren Yo. I animasjonen blir det også advart om at den opprinnelige hastigheten ikke har noen vertikal komponent, men når den faller, øker denne komponenten jevnt, takket være handlingen av g, tyngdekraftsakselerasjon.

Når det gjelder den horisontale hastighetskomponenten, forblir den konstant mens bevegelsen varer.

I henhold til det som er sagt, er posisjoner etablert som en funksjon av tid, både på den horisontale aksen og i den vertikale aksen. Høyre er tatt som +x -aksen, mens nede er adressen -og. Verdien av tyngdekraften er G = -9.8 m/s² enten -32 fot/s²:

x (t) = x_enten + v_okse.T (horisontal posisjon); v_okse det er konstant

og (t) = y_enten + v_Oy.T - ½ g.t² (vertikal stilling); v_og = v_Oy - g.T (vertikal hastighet)

Posisjon, hastighet, flytid og maksimal horisontalt område

Ligningene er forenklet hvis de velger følgende startposisjoner: x_enten = 0, og_enten = 0 på lanseringsstedet. I tillegg v_Oy = 0, Siden mobilen er projisert horisontalt. Med dette valget er bevegelsesligningene som dette:

x (t) = v_okse.t; v_x = v_okse

og (t) = - ½ g.t²; v_og = - g.t

Når tiden ikke er tilgjengelig, er ligningen som relaterer hastigheter og forskyvninger nyttig. Dette er gyldig for vertikal hastighet, siden den horisontale forblir konstant gjennom bevegelsen:

Kan tjene deg: kalsiumfluor (CAF2): Struktur, egenskaper, bruk

v_og² = v_Oy² + 2.g .y = 2.g.og

Flytid

Å beregne Flytid t_flygning, Anta at mobilen er projisert fra en høyde H På gulvet. Ettersom referansesystemets opprinnelse på lanseringspunktet er valgt, når det når bakken, er den i posisjon -H. Erstatte dette i ligning 2) det oppnås:

-H = - ½ g.t²_flygning

t_flygning = (2H/g)^½

Maksimal rekkevidde

Han Horisontal rekkevidde Denne gangen oppnås ved å erstatte x (t):

x_Maks = v_okse. (2H/g)^½

Løste øvelser

-Trening løst 1

Et helikopter flyr horisontalt, og opprettholder en konstant høyde på 580 m når den frigjør en boks som inneholder mat på en flyktningleir. Boksen lander i en horisontal avstand på 150 m fra lanseringen. Finn: a) flytid for boksen.

b) Helikopterets hurtighet.

c) hvor raskt boksen berøres?

Løsning

a) Høyden h som maten frigjøres fra er h = 500 m. Med disse dataene når du erstatter får du:

t_flygning = (2H/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) Helikopteret bærer den horisontale starthastigheten v_okse av pakken og siden en av dataene er x_Maks:

x_Maks = v_okse. (2H/g)^½ ® v_okse = x_Maks /(2H/g)^½= x_Maks / t_flygning = 150 m/ 10.9 S = 13.8 m/s

C) Prosjektilets hastighet når som helst er:

v_og = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/t

Det negative tegnet indikerer at mobilen beveger seg nedover.

-Trening løst 2

Fra et fly som flyr horisontalt i en høyde H = 500 m og 200 km/t En pakke faller som må falle på et åpent kjøretøy som marsjerer til 18 km/t på veien. I hvilken posisjon skal flyet la pakken falle i kjøretøyet? Ikke ta hensyn til luftmotstand eller vindhastighet.

Kan tjene deg: dimensjonal analyseFigur 2. Ordning for øvelsen løst 2. Kilde: Utarbeidet av F. Zapata.

Løsning

Det er praktisk å først overføre alle enheter til det internasjonale systemet:

18 km/t = 6 m/s

200 km /t = 55 m /s

Det er to mobiler: fly (1) og kjøretøy (2), og det er nødvendig å velge et koordinatsystem for å finne dem begge. Det er praktisk å gjøre det på utgangspunktet for pakken på flyet. Pakken projiseres horisontalt med hastigheten som flyet bærer: v₁, Mens kjøretøyet beveger seg til v₂ antatt konstant.

-Fly

Opprinnelig stilling: x = 0; y = 0

Opprinnelig hastighet = v₁ (horisontal)

Posisjonslikninger: og (t) = -½g.t²  ; x (t) = v₁.t

-Kjøretøy

Startposisjon: x = 0, y = -h

Opprinnelig hastighet = v₂  (konstant)

x (t) = x_enten + v₂. t

Tiden som pakkeflyet varer er:

t_flygning = (2H/g)^½ = (2 × 500/9.8)^½S = 10.1 s

På dette tidspunktet har pakken opplevd en horisontal forskyvning av:

x_Maks = v_okse . (2H/g)^½= 55 m/s x 10.1 s = 556 m.

På dette tidspunktet har kjøretøyet også beveget seg horisontalt:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Hvis flyet slipper pakken umiddelbart som kjøretøyet ser transitt under den, vil det ikke kunne falle rett inn i den. For at det skal skje, må han kaste det tilbake:

D = 556 m - 60.6 m = 495.4 m.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 74-84.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).117 - 164.
3. Prosjektil bevegelse. Gjenopprettet fra: Phys.Librettexts.org.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 53-58.
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill. 126-131.