Obliske parabolske skuddegenskaper, formler, ligninger, eksempler

Han Oblisk parabolsk skudd Det er et spesielt tilfelle av fritt fallbevegelse der prosjektilets opprinnelige hastighet danner en viss vinkel med det horisontale, noe som resulterer i en parabolsk bane.

Det frie fallet er et tilfelle av bevegelse med konstant akselerasjon, der akselerasjon er tyngdekraften, som alltid peker vertikalt ned og har en styrke på 9,8 m/s^2. Det avhenger ikke av deigen til prosjektilet, som Galileo Galilei demonstrerte i 1604.

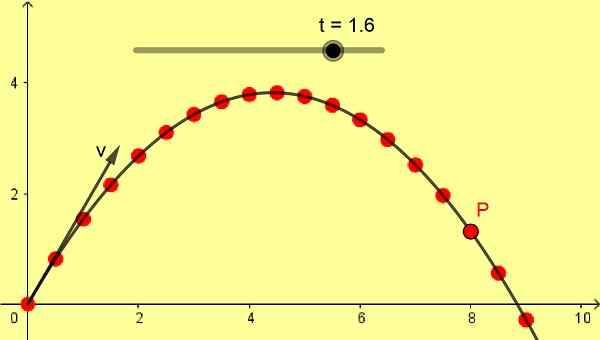Figur 1. Oblisk parabolsk skudd. (Egen utdyping)

Hvis den innledende prosjektilhastigheten er vertikal, har fritt fall en rett og vertikal bane, men hvis den opprinnelige hastigheten er skrå, er banen til fritt fall en parabolsk kurve, også demonstrert av Galileo.

Eksempler på parabolsk bevegelse er banen som følger en baseball, kulen avfyrt av en kanon og vannstrålen som kommer ut av en slange.

Figur 1 viser et skrå parabolsk skudd på 10 m/s med en vinkel på 60º. Skalaen er i meter og de påfølgende P -stillingene blir tatt med en forskjell på 0,1 s fra det første øyeblikket 0 sekunder.

[TOC]

Formler

Bevegelsen av en partikkel er fullstendig beskrevet hvis dens posisjon er kjent, dens hastighet og dens akselerasjon som en funksjon av tid.

Den parabolske bevegelsen som følge av et skrå skudd er superposisjonen av en horisontal bevegelse med konstant hastighet, pluss en vertikal bevegelse med konstant akselerasjon lik akselerasjonen av tyngdekraften.

Formlene som gjelder for det skrå parabolske skuddet er den som tilsvarer en bevegelse med konstant akselerasjon a = g, Legg merke til at fet skrift har blitt brukt for å indikere at akselerasjon er en vektormengde.

Kan tjene deg: naturlige satellitter

Posisjon og hastighet 

I en konstant akselerasjonsbevegelse avhenger posisjonen matematisk av tid på en kvadratisk måte.

Hvis vi betegner r(T) Posisjonen til tiden t, renten Den første øyeblikkelige stillingen, venten Den første hastigheten, g akselerasjon og t = 0 Som det første øyeblikket formelen som gir posisjonen for hvert øyeblikk av tid t er:

r(t) = r_enten + v_enten T + ½ g t²

Fet i forrige uttrykk indikerer at det er en vektorligning.

Hastigheten som en funksjon av tid oppnås ved å ta derivatet med hensyn til t av posisjonen og resultatet er:

v(t) = v_enten + g t

Og for å oppnå akselerasjon som en funksjon av tiden, er hastigheten avledet fra t resulterende:

til(t) = g

Når tiden ikke er tilgjengelig, er det et forhold mellom hastighet og posisjon, som er gitt av:

v² = venten² - 2 g (og - meg)

Ligninger

Neste finner vi likningene som gjelder for et skrå parabolsk skudd i kartesisk form.

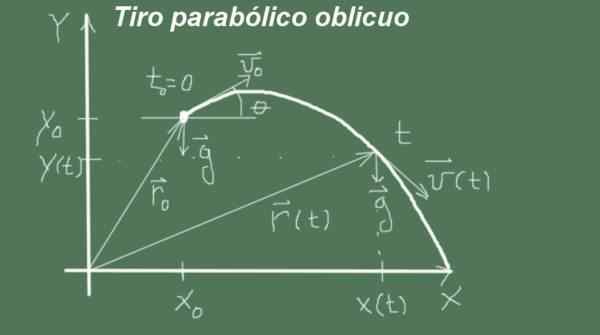
Figur 2. Variabler og parametere for det skrå parabolske skuddet. (Egen utdyping)

Bevegelsen begynner for øyeblikket t = 0 Med startposisjon (Xo, meg) og størrelseshastighet venten og vinkel θ, det vil si at den innledende hastighetsvektoren er (venten cosθ, venten Senθ). Bevegelsen passerer med akselerasjon 

g = (0, -g).

Parametriske ligninger

Hvis vektorformelen som gir posisjon som en funksjon av tid, blir brukt og komponenter blir gruppert og utjevnet, vil ligningene gitt av koordinatene til posisjonen til når som helst tid t oppnås.

x (t) = x_enten + v_okse t 

og (t) = y_enten + v_Oy t -½ g t²

Tilsvarende er ligninger hatt for hastighetskomponenter som en tidsfunksjon.

Det kan tjene deg: Normal innsats: Hva den består av, hvordan det beregnes, eksempler

v_x(t) = v_okse

v_og(t) = v_Oy - g t 

Hvor: v_okse = venten cosθ; v_Oy = venten Senθ

Bane ligning

y = a x^2 + b x + c

A = -g/(2 vokse^2)

B = (vOy/vokse + g xenten/vokse^2)

C = (ogenten - vOy xenten / vokse)

Eksempler 

Eksempel 1

Svar på følgende spørsmål:

a) Hvorfor i parabolsk skyteproblemer forakter vanligvis effekten av friksjon med luft?

b) gjør formen på objektet i det parabolske skuddet?

Svar

a) For bevegelse av et prosjektil å være parabolisk er det viktig at luftfriksjonskraften er mye lavere enn vekten til objektet som lanseres. 

Hvis en korkball eller noe lett materiale kastes, kan friksjonskraften sammenlignes med vekten og dens bane kan ikke nærme seg en parabola.

Tvert imot, hvis det er en tung gjenstand som en stein, er friksjonskraften ubetydelig sammenlignet med vekten av steinen og dens bane gjør nær en parabola.

b) Formen på objektet som lanseres er også relevant. Hvis en plata med fly i form av en avionncito lanseres, vil bevegelsen ikke være fri eller parabolsk, siden formen favoriserer luftmotstand.

På den annen side, hvis det samme papiret er kompakt i form av en ball, er den resulterende bevegelsen veldig lik en parabola.

Eksempel 2

Et prosjektil lanseres fra det horisontale gulvet raskt på 10 m/s og 60º vinkel. Dette er de samme dataene som figur 1 ble utviklet. Med disse dataene finner jeg:

a) øyeblikk der det når maksimal høyde.

Kan tjene deg: Hva er de termiske egenskapene og hva som er? (Med eksempler)

b) maksimal høyde.

c) Hastigheten i maksimal høyde.

d) posisjon og hastighet ved 1,6 s.

e) I det øyeblikket han spiller jord igjen.

f) Horisontalt omfang.

Løsning på)

Den vertikale hastigheten avhengig av tid er

v_og(t) = v_Oy - G t = v_enten Senθ - g t = 10 sen60º - 9.8 t = 8.66 - 9.8 t 

På det tidspunktet er den maksimale høyden nådd den vertikale hastigheten er null et øyeblikk.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Løsning B)

Maksimal høyde er gitt av koordinaten og For øyeblikket hvor den høyden er nådd:

og (0.88s) = Yo jeg vil t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Derfor er maksimal høyde 3.83 m.

Løsning C)

Hastigheten i maksimal høyde er horisontal:

v_x(t) = v_okse = v_enten cosθ = 10 cos60º = 5 m/s 

D) Løsning

Stillingen på 1.6 s er:

X (1.6) = 5*1,6 = 8,0 m

og (1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Løsning e)

Når koordinaten berører og den blir kansellert, så:

og (t) = 8.66*T -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Løsning f)

Det horisontale omfanget er X -koordinaten rett i det øyeblikket som spiller jord:

X (1.77) = 5*1,77 = 8,85 m

Eksempel 3

Finn bane -ligningen med eksempel 2 data.

Løsning 

Den parametriske ligningen for banen er:

x (t) = 5*t

og (t) = 8.66*T -½ 9.8 t^2

Og den kartesiske ligningen oppnås ved å rydde t av den første og erstatte i den andre

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Forenkle:

y = 1,73 x - 0,20 x^2 

Referanser

1. P. P. Teodorescu (2007). "Kinematikk". Mekaniske systemer, klassiske modeller: Partikkelmekanikk. Springer.
2. Resnick, Halliday & Krane (2002). Fysikkvolum 1. Cecsa, Mexico.
3. Thomas Wallace Wright (1896). Elementer av mekanikk inkludert kinematikk, kinetikk og statistikk. E og fn spon.
4. Wikipedia. Parabolsk bevegelse. Gjenopprettet fra Es.Wikipedia.org.
5. Wikipedia. Prosjektil bevegelse.Innhentet fra.Wikipedia.org.