Mekanisk arbeid hva er, forhold, eksempler, øvelser

Han Mekanisk arbeid Det er definert som endringen i energitilstanden til et system, forårsaket av virkningen av ytre krefter som tyngdekraft eller friksjon. De mekaniske arbeidsenhetene i det internasjonale systemet (SI) er Newton X Metro eller Joules, forkortet av J.

Matematisk er det definert som skalarproduktet av kraftkraften av vektorforskyvningen. Ja F Det er den konstante kraften og l Det er forskyvningen, begge vektorene, arbeidet w uttrykkes som: W = F ● l

Figur 1. Mens utøveren øker vekten, jobber han mot tyngdekraften, men når han opprettholder vekten ubevegelig, fra fysikkens synspunkt, gjør han ikke arbeid. Kilde: Needpix.com

Når styrken ikke er konstant, må vi analysere arbeidet som er gjort når forskyvningene er veldig små eller differensielle. I dette tilfellet, hvis det anses som et utgangspunkt for punkt A og som ankomst til B, oppnås det totale arbeidet ved å legge til alle bidrag til det samme. Dette tilsvarer å beregne følgende integral:

Og som det fremgår av begynnelsen, forutsatt at det er en endring i systemenergi, vil det være fordi det er krefter fra utlandet som handler på det, derfor:

Variasjon i systemenergi = arbeid utført av eksterne krefter

ΔE = w_ext

Når energi legges til systemet, w> 0 og når det trekkes fra<0. Ahora bien, si ΔE = 0, puede significar que:

-Systemet er isolert og det er ingen ytre krefter som virker på det.

-Det er eksterne krefter, men de jobber ikke med systemet.

Siden variasjonen i energi tilsvarer arbeidet utført av eksterne krefter, hvis energien også er Joule. Dette inkluderer alle typer energi: kinetisk, potensial, termisk, kjemisk og mer.

[TOC]

Forhold for at det skal være mekanisk arbeid

Vi har allerede sett at arbeidet er definert som et skalarprodukt. La oss ta definisjonen av arbeid utført av konstant kraft og anvende konseptet med skalarprodukt mellom to vektorer:

W = F ● L = F.l.cos θ

Hvor F Det er styrken på styrken, l Det er størrelsen på forskyvning og θ Det er vinkelen som eksisterer mellom kraft og forskyvning. I figur 2 er det et eksempel på skrå ekstern kraft som virker på en blokk (systemet), som produserer en horisontal forskyvning.

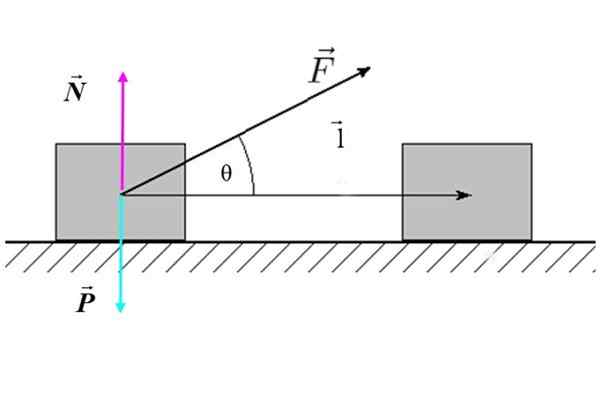Figur 2. Gratis kroppsdiagram over en blokk som beveger seg på en flat overflate. Kilde: f. Zapata.

Omskriving av arbeidet som følger:

W = (f. cos θ). l

Vi kan bekrefte at bare komponenten i styrken er parallell med forskyvningen: F. cos θ eer i stand til å gjøre arbeid. Hvis θ = 90º, så vil cos θ = 0 og arbeidet være ugyldig.

Derfor konkluderes det med at krefter vinkelrett på forskyvning ikke gjør mekanisk arbeid.

I tilfelle av figur 2, og heller ikke normalkraft N heller ikke vekten P De fungerer, fordi begge er vinkelrett på forskyvning l.

Tegn på arbeid

Som forklart ovenfor, W Det kan være positivt eller negativt. Når Cos θ> 0, Arbeidet som er utført med makt er positivt, siden det har samme retning av bevegelsen.

Det kan tjene deg: Massenummer: Hva er det og hvordan du får det (med eksempler)

Ja cos θ = 1, Styrke og forskyvning er parallell og arbeidet er maksimalt.

I tilfelle cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Når cos θ = -1, Kraften er helt motsatt av forskyvning, for eksempel kinetisk friksjon, hvis virkning er å stoppe objektet den fungerer. Så arbeidet er minimalt.

Dette stemmer overens med det som ble sagt i begynnelsen: Hvis arbeidet er positivt, blir energi lagt til systemet, og hvis det er negativt, blir det trukket fra.

Nettverk W_nett Det er definert som summen av verkene som er utført av alle krefter som virker på systemet:

W_nett = ∑W_Yo

Da kan vi konkludere med at for å garantere eksistensen av nettmekanisk arbeid, er det nødvendig at:

-Eksterne krefter virker på objektet.

-Disse kreftene er ikke alle vinkelrett på forskyvningen (cos θ ≠ 0).

-Verkene som er utført av hver styrke blir ikke kansellert med hverandre.

-Det er en forskyvning.

Mekaniske arbeidseksempler

-Hver gang det kreves å sette et objekt i bevegelse basert på hvile, er det nødvendig å utføre mekanisk arbeid. Skyv for eksempel kjøleskap eller en tung bagasjerom på en horisontal overflate.

-Et annet eksempel på en situasjon der det er nødvendig å utføre mekanisk arbeid er å endre hastigheten på en bevegelig ball.

-Det er nødvendig å gjøre arbeid for å heve et objekt i en viss høyde på gulvet.

Nå er det like vanlige situasjoner der Nei Arbeidet er utført, selv om opptredener indikerer noe annet. Vi har sagt at for å heve et objekt i en viss høyde, må vi gjøre arbeid, så vi laster inn objektet, vi løfter det over hodet og holder det der. Gjør vi arbeid?

Tilsynelatende ja, for hvis objektet er tungt, blir armene imidlertid slitne snart, uansett hvor mye arbeid som gjøres, blir det ikke gjort arbeid fra fysikkens synspunkt. Hvorfor ikke? Fordi objektet ikke beveger seg.

En annen sak der den, til tross for at den har en ekstern styrke, ikke utfører mekanisk arbeid, er når partikkelen har en jevn sirkulær bevegelse.

Det kan tjene deg: Normal innsats: Hva den består av, hvordan det beregnes, eksempler

For eksempel et barn som vender en stein bundet til en streng. Spenningen av strengen er den sentripetale kraften som tillater rotasjon av steinen. Men til enhver tid er denne kraften vinkelrett på forskyvning. Ikke gjør mekanisk arbeid, til tross for at det favoriserer bevegelse.

Arbeidsenergi-teorem-kinetikken

Den kinetiske energien i systemet er hva det har under bevegelsen. Ja m er deigen og v Det er bevegelseshastigheten, kinetisk energi betegnes av K Og det er gitt av:

K = ½ mv²

Per definisjon kan ikke den kinetiske energien til et objekt være negativ, siden både massen og kvadratet på hastigheten alltid er positive mengder. Kinetisk energi kan være 0, når objektet er i ro.

For å endre den kinetiske energien til et system, er det nødvendig-. For dette er det nødvendig å gjøre nettarbeid på systemet, derfor:

W_nett = ΔK

Dette er arbeidsteoremet - kinetisk energi. Stater som:

Nettoarbeid tilsvarer endringen i systemets kinetiske energi

Merk at selv om K alltid er positiv, kan ΔK være positiv eller negativ, siden:

Δk = k_endelig - K _første

Ja K_endelig >K _første Systemet har fått energi og Δk> 0. Tvert imot, ja K_endelig < K _første, Systemet har gitt energi.

Arbeid utført for å strekke en vår

Når du strekker seg (eller komprimerer) en fjær, er det nødvendig å gjøre en jobb. Dette arbeidet lagres om våren, slik at dette igjen kan jobbe med, for eksempel, en blokk som er festet til en av dens mål.

Hooke's lov uttaler at styrken som utøves av en vår er en restitusjonsstyrke - det er i strid med forskyvning - og også proporsjonal med nevnte forskyvning. Proporsjonalitetskonstanten avhenger av hvordan våren er: myk og lett deformerbar eller stiv.

Denne styrken er gitt av:

F_r = -kx

I uttrykket, F_r Det er styrken, k Det er fjærkonstanten og x Det er forskyvningen. Det negative tegnet indikerer at kraften utøver av våren motsetter seg forskyvning.

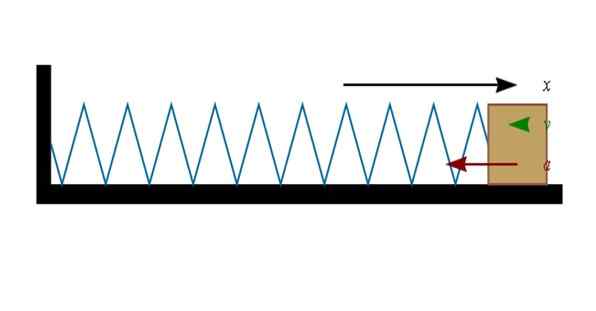Figur 3. En komprimert eller strukket vår fungerer på et objekt bundet til slutten. Kilde: Wikimedia Commons.

Hvis fjæren er komprimert (til venstre i figuren), vil blokken på enden bevege seg til høyre. Og når våren er strukket (til høyre), vil blokken ønske å bevege seg til venstre.

For å komprimere eller strekke fjæren, må noen eksterne agenter gjøre jobben, og ettersom det er en variabel kraft, for å beregne dette arbeidet, må du bruke definisjonen som skjedde i begynnelsen:

Kan tjene deg: darcy lov

Det er veldig viktig å merke seg at dette er arbeidet som er utført av den eksterne agenten (for eksempel hånden til en person) for å komprimere eller strekke våren. Det er derfor det negative tegnet ikke vises. Og ettersom posisjonene er firkantede, uansett om de er kompresjoner eller forlengelser.

Arbeidet som vil gjøre våren etter tur på blokken er:

W_vår = -W_ext

Øvelser

Oppgave 1

Blokken i figur 4 har masse M = 2 kg og glir gjennom det skrå planet uten friksjon, med α = 36.9. Forutsatt at det er lov å skli fra resten fra toppen av flyet, hvis høyde er H = 3 m, finner du hastigheten som blokken når basen av flyet, gjennom arbeidsenergi-teoremenergi kinetisk.

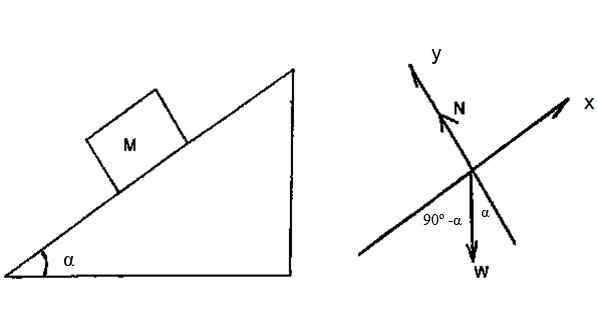Figur 4. En blokk glir ned på et skrå fly uten å gni. Kilde: f. Zapata.

Løsning

Det frie kroppsdiagrammet viser at den eneste kraften som kan gjøre arbeid på blokken er vekten. Mer presis: Vektkomponenten langs x -aksen.

Avstanden som ble reist av blokken på flyet beregnes med trigonometri:

D = 3 / (cos 36.9º) m = 3.75 m

W_vekt = (Mg). d. cos (90-a) = 2 x 9.8 x 3.75 x cos 53.1. J = 44.1 J

Ved å jobbe teorem-energi kinetisk:

W_nett = ΔK

W_nett = W_vekt

Δk = ½ mv_F²- ½ mv_enten²

Siden den frigjøres fra hvile, v_enten = 0, derfor:

W_nett = ½ mv_F²

Oppgave 2

En horisontal fjær, hvis konstant er k = 750 N/m er fikset i den ene enden til en vegg. Den ene personen komprimerer den andre enden en avstand på 5 cm. Beregn: a) Kraften utøvd av personen, b) arbeidet han gjorde for å komprimere våren.

Løsning

a) Størrelsen på kraften som er brukt av personen er:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Hvis vårenden opprinnelig er i x₁ = 0, for å ta det derfra til sluttposisjonen x₂ = 5 cm, det er nødvendig å gjøre følgende arbeid, i henhold til resultatet oppnådd i foregående avsnitt:

W_ext = ½ k (x₂² - x₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 2. Dynamisk. Redigert av Douglas Figueroa (USB).
2. Iparraguirre, l. 2009. Grunnleggende mekanikk. Naturvitenskapssamling og matematikk. Gratis online distribusjon.
3. Knight, r. 2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. FYSIKK LIBRETTEXTS. Arbeidsenergi-teorem. Gjenopprettet fra: Phys.Librettexts.org
5. Arbeid og energi. Gjenopprettet fra: Fysikk.Bu.Edu
6. Arbeid, energi og kraft. Gjenopprettet fra: ncert.Nic.i