Fourier transformasjonsegenskaper, applikasjoner, eksempler

De Fourier Transform Det er en metode for analytisk tilstrekkelig orientert til integrerbare funksjoner som tilhører familien til tOmfattende ransformert. Den består av en omdefinisjon av funksjoner F (t) Når det gjelder COS (T) og SEN (T).

De trigonometriske identitetene til disse funksjonene, sammen med deres avledning og antiderivasjonsegenskaper, tjener til å definere Fouriers transformasjon gjennom følgende komplekse funksjon:

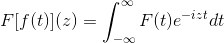
Som er oppfylt mens uttrykket er fornuftig, det vil si når den upassende integralen er konvergent. Algebraisk sies det at Fouriers transformasjon er en lineær homeomorphism.

Enhver funksjon som kan arbeides med Fourier Transform, må presentere ugyldighet utenfor en definert parameter.

[TOC]

Egenskaper

Kilde: Pexels

Fourier -transformasjonen oppfyller følgende egenskaper:

Eksistens

For å bekrefte eksistensen av Fourier -transformasjonen til en f (t) -funksjon definert i Royals R, Følgende to aksiomer må være oppfylt:

1. f (t) er kontinuerlig i stykker for alt R
2. f (t) er integrerbar i R

Fourier transformasjon linearitet

La M (t) og N (t) to to funksjoner med definert Fourier transformert, med konstanter A og B alle.

F [A m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Som også er avhengig av lineariteten til integralen med samme navn.

Fourier forvandlet fra et derivat

Du har en funksjon F  som er kontinuerlig og integrerbar i all reais, hvor:

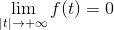
Og derivat av F (f ') Det er kontinuerlig og definert i stykker i alt R

Fourier -transformasjonen av et derivat er definert av integrasjon av deler, av følgende uttrykk:

F [f '(t)] (z) = izF [f (t)] (z)

I avledninger av høyere orden vil det bli brukt på en homolog måte, hvor du for alle n 1 må du:

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Differensiering av Fourier -transformasjonen

Du har en funksjon F  som er kontinuerlig og integrerbar i all reais, hvor:

I (d/dz)F [f (t)] (z) = F  [t .  f (t)] (z)

Fourier forvandlet fra en oversettelse

For alle θ som tilhører et sett og T Det tilhører settet S ', du må:

F [ τ_til θ] =  og^-IAY F [ θ]                                 F [ τ_tilT ] =  og^-Iax  F [ T]   

Med  τ_til  fungerer som oversettelsesoperatør på vektoren til.

Oversettelse av Fourier -transformasjonen

For alle θ som tilhører et sett og T Det tilhører settet S ', du må:

τ_til F [θ] =  F [og^-Iax.θ]                                τ_til F [t ] =  F [og^-IAY . T]

Kan tjene deg: Hypercubo: Definisjon, dimensjoner, koordinater, utfoldet

For alle til som tilhører R

Fourier Transform of a Scale Group

For alle θ som tilhører et sett S. T som tilhører settet s '

λ tilhører R - 0  Du må:

F [θ (λx)] = (1 / | λ |) F [θ] (og/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (og/λ)

Ja F Det er en kontinuerlig og rent integrerbar funksjon, der a> 0. Så:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

For å demonstrere dette resultatet, kan vi fortsette med endring av variabel.

Når t → + så s = AT → + ∞

Når t → - så s = AT → - ∞

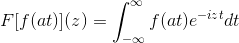
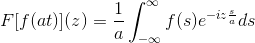
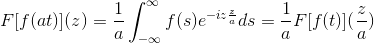
Symmetri

For å studere symmetrien til Fourier Transforma.

Du har θ og Δ som tilhører S. Derfra kan det trekkes ut at:

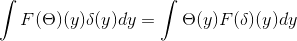
Å skaffe

1 / (2π)^d  F [θ ], F [Δ] ParseVal identitet

1 / (2π)^D/2  || F [θ ] ||_L²_R^d     Plancherel Formula

Fourier forvandlet fra et produkt til konvolusjon

Å jage lignende mål som i Laplace -transformasjonen, konvolusjon av funksjoner refererer til produktet mellom Fourier -transformasjonene.

Den har F og G som 2 funksjoner begrenset, definert og helt integrerbar:

F (f *g) = f (f) . F (g)

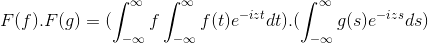
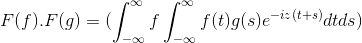
Så når du gjør endringen av variabel

t + s = x; Dobbelt integral dobbeltintegral videreføres

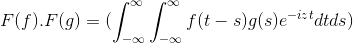
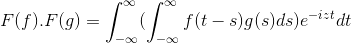
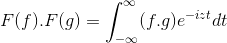
F (f) . F (g) = f (f . g)

Kontinuitet og fall i uendelig

For alle θ som tilhører R, f [ θ] adlyder kriteriene for kontinuerlig funksjon begrenset i r^d.

Også F [ θ] (y) → 0 i C si | y | → ∞

Historie

Dette matematiske konseptet ble presentert av Joseph B. Fourier i 1811 mens han utviklet en traktat om Varme spredt. Det ble raskt adoptert av forskjellige grener av vitenskap og ingeniørfag.

Det ble etablert som hovedarbeidsverktøyet i studiet av ligninger med delvis derivater, og sammenlignet selv med arbeidsforholdet mellom Laplace transformerte og vanlige differensialligninger.

Hva er Fourier -transformasjonen for?

Det tjener hovedsakelig til betydelige ligninger, mens transformering av uttrykk avledet til kraftelementer, som betegner differensielle uttrykk i form av integrerbare polynomer.

I optimalisering, modulering og modellering av resultater fungerer det som et standardisert uttrykk, og er en hyppig ressurs for prosjektering etter flere generasjoner.

Fouriers serie

De er definert serier når det gjelder cosen og bryster; De tjener til å lette arbeidet med generelle periodiske funksjoner. Når de brukes, er de en del av oppløsningsteknikkene for delvise og vanlige differensialligninger.

Det kan tjene deg: ekte ekte variabel funksjon og dens grafiske representasjon

Fourier -serien er enda mer generelle enn Taylors serie, fordi de utvikler periodiske Discontinua -funksjoner som ikke har noen representasjon i Taylor Series.

Andre former for Fourier -serien

Å analytisk forstå Fourier -transformasjonen er det viktig.

-Fourier -serien på en 2L -periodefunksjon

Mange ganger er det nødvendig å tilpasse strukturen i en Fourier-serie, til periodiske funksjoner hvis periode er p = 2l> 0 i intervallet [-l, l].

-Fourier -serien i jevn og rare funksjoner

Intervallet [-π, π] vurderes som gir fordeler når du utnytter funksjonens symmetriske egenskaper.

Hvis f er dreiemoment, er Fourier -serien etablert som en serie Cosenos.

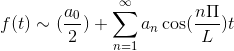
Hvis F er merkelig, er Fourier -serien etablert som en serie bryster.

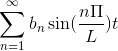
-Kompleks notasjon av Fourier -serien

Hvis du har en F (t) -funksjon, som oppfyller alle de utviklede kravene i Fourier-serien, er det mulig å betegne den i intervallet [-t, t] ved å bruke dens komplekse notasjon:

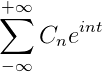
applikasjoner

Kilde: Pexels

Beregning av den grunnleggende løsningen

Fouriers transform. Søk om funksjoner med domener ikke begrenset likt.

I likhet med Laplace -transformasjonen, transformerer Fourier -transformasjonen en funksjon av delvise derivater, til en vanlig differensialligning mye lettere å betjene.

Cauchys problem for varme ligningen presenterer et hyppig anvendelsesfelt av Fourier -transformasjonen der funksjonen genereres Dirichlet Heat eller Core Nucleus.

Når det gjelder beregningen av den grunnleggende løsningen, presenteres følgende tilfeller der det er vanlig å finne Fourier -transformasjonen:

-Laplace ligning

-Varm ligning

-Schrödinger ligning

-Bølge ligning

Signalteori

Den generelle årsaken til anvendelsen av Fourier -transformasjonen i denne grenen skyldes stort sett den karakteristiske nedbrytningen av et signal som en uendelig overlapping av lettere behandlingsbare signaler.

Det kan være en lydbølge eller en elektromagnetisk bølge, Fourier -transformasjonen uttrykker den i en enkel bølger overlapp. Denne representasjonen er ganske hyppig i elektroteknikk.

Kan tjene deg: vertikal linje

På den annen side er de eksempler på anvendelse av Fourier -transformasjonen innen signalteori:

-Systemidentifikasjonsproblemer. Etablert f og g

-Problem med konsistensen av utgangssignalet

-Problemer med signalfiltrering

Eksempler

Eksempel 1

Definer Fourier -transformasjonen for følgende uttrykk:

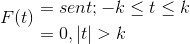
Vi kan også representere det som følger:

F (t) = Sin (t) [h_{(T + K)} - H_{(T - K)} ]

Rektangulær puls er definert:

p (t) = h_{(T + K)} - H_{(T - K)}

Fourier Transform brukes på neste uttrykk som ligner modulasjonsteorem.

f (t) = p (t) sin (t)

Hvor: F [w] = (1/2) I [P (W + 1) - P (W - 1)]

Og Fourier -transformasjonen er definert av:

F [w] =  (1/2) I [(2/2W+1) Sen (K (W+1)) - (2/2W+1) Sen (K (W-1))]

Eksempel 2

Definer Fourier -transformasjonen for uttrykk:

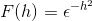Per definisjon uttrykker vi transformasjonen som følger

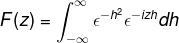
Fordi f (h) er en jevn funksjon, kan det bekreftes det

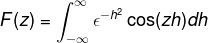Avleder innen integralet med hensyn til z, kan uttrykket skrives om. Dette trinnet er betydelig i arbeid med differensialligninger.

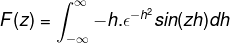
Integrering av deler brukes ved å velge variablene og deres differensialer som følger

u = sin (zh) du = z cos (zh) dh

dv = h (e^-h)²                       V = (e^-h)² / 2

Erstatte den

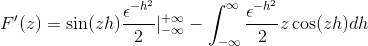
Etter å ha evaluert under den grunnleggende beregningsteoremet

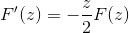
Bruker forkunnskap relatert til differensialligningene i første orden, er uttrykket betegnet som

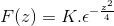
For å få k evaluerer vi 

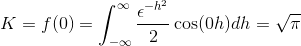
Endelig er Fouriers transformasjon definert som

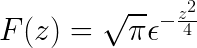
Foreslåtte øvelser

• Bestem uttrykket Fourier Transform
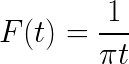
• Løs følgende feil integral ved hjelp av Paresevals likhet
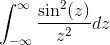
• Få transformasjonen av uttrykket w/(1+w²)

Referanser

1. Duoandikoetxea zuazo, j., Fourier -analyse. Addison- Wesley Iberoamericana, Autonomous University of Madrid, 1995.
2. Lions, J. L., Matematisk analyse og numeriske metoder for vitenskap og teknologi. Springer-Verlag, 1990.
3. Lieb, e. H., Gaussiske kjerner har bare gaussiske maksimaliserere. Finne opp. Matte. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Fourier -serier og integraler. Academic Press, New York, 1972.
5. Schwartz, l., Théorie des Distribusjoner. Ed. Hermann, Paris, 1966.