Hjemmeside
Matte
Rektangel trapesegenskaper, forhold og formler, eksempler

Matte

Rektangel trapesegenskaper, forhold og formler, eksempler

2743
242
Marius Aasen

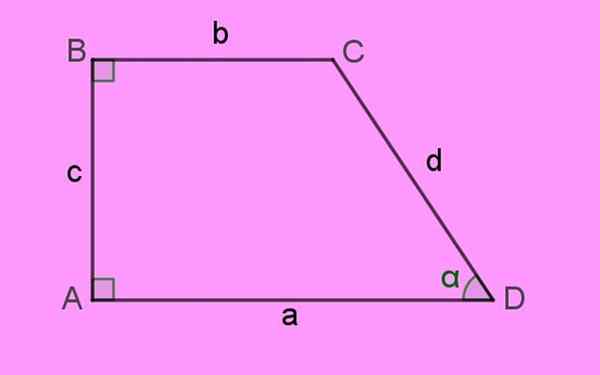
EN Rektangel trapes Det er en flat figur på fire sider, slik at to av dem er parallelle med hverandre, kalt baser Og også en av de andre sidene er vinkelrett på basene.

Av denne grunn er to av de indre vinklene rette, det vil si de måler 90º. Derav navnet "rektangel" som er gitt til figuren. Følgende bilde av et rektangel trapes avklarer disse egenskapene:

[TOC]

Elementer av trapes

Elementene i trapesiden er:

-Baser

-Hjørner

-Høyde

-Interne vinkler

-Gjennomsnittlig base

-Diagonaler

Vi vil detaljere disse elementene ved hjelp av figur 1 og 2:

Figur 1. Et rektangel trapes, preget av å ha to indre vinkler på 90º: A og B. Kilde: f. Zapata.

Sidene av rektangelet trapesoid er betegnet med små bokstaver A, B, C og D. Hjørnene på figuren eller Hjørner De er indikert med store bokstaver. Endelig Interne vinkler De kommer til uttrykk med greske bokstaver.

I følge definisjonen er baser Av denne trapezoid er sider A og B, som som observert er parallelle og har også forskjellig lengde.

Den vinkelrett siden til begge basene er siden c til venstre, som er høyde h av trapesen. Og til slutt er det side D, som danner den akutte vinkelen α med siden A.

Summen av Interne vinkler av en firkantet er 360º. Det blir lett verdsatt at den manglende vinkelen C i figuren er 180 - α.

De Gjennomsnittlig base Det er segmentet som blir med midt på sidene av ikke -parallelle sider (EF -segment i figur 2).

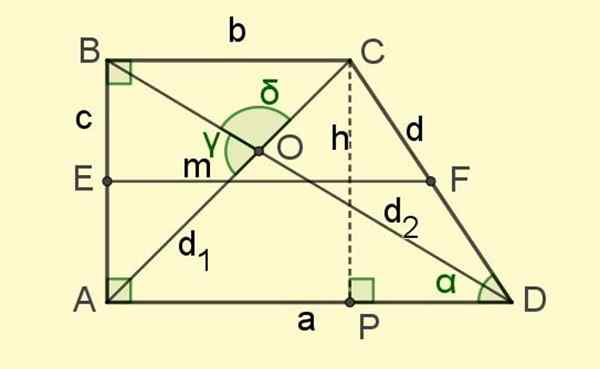Figur 2. Elementene i rektangelet trapesidzoid. Kilde: f. Zapata.

Og til slutt er det diagonalene d₁ og d₂, Segmentene som forener de motsatte toppunktene og som krysser hverandre på punkt O (se figur 2).

Relasjoner og formler

Høyde H på trapesiden

H = c

Omkrets s

Det er målet på konturen og beregnes ved å legge til sidene:

Omkrets = A + B + C + D

Siden d Det kommer til uttrykk i form av høyde eller side c Gjennom Pythagoras -teoremet:

D = √ (A-B)² + c²

Erstatter i omkretsen:

P = A + B + C + √ (A-B)² + c²

Gjennomsnittlig base

Det er semi -kroppene til basene:

Medium base = (a+b)/2

Noen ganger blir den gjennomsnittlige basen uttrykt på denne måten funnet:

Medium base = (hovedbase + mindre base) /2

Område

Område A i trapesen er et produkt av gjennomsnittlig base etter høyde:

A = (Hovedbase + mindre base) x høyde /2

A = (a+b) c/2

Diagonaler, sider og vinkler

Flere trekanter vises i figur 2, både rektangler og ikke -nektangler. For de som har rett trekanter, kan de brukes av Pythagoras -teoremet og de som ikke gjør det, teoremene til kosinus og bryst.

Kan tjene deg: transcendente tall: hva er, formler, eksempler, øvelser

På denne måten er det sammenhenger mellom sidene og mellom sidene og de indre vinklene til Trapezio.

CPA -trekant

Det er rektangel, bena er de samme og de er verdt B, mens hypotenusen er den diagonale d₁, derfor:

d₁² = b² + b² = 2b²

Dab Triangle

Det er også rektangel, beina er til og c (eller også til og h) Og hypotenusen er d₂, så det:

d₂² = a² + c²= a² + h²

CDA -trekant

Siden denne trekanten ikke er rektangel, blir kosinusteoremet påført, eller også brystet.

I følge Coseno -teorem:

d₁² = a² + d² - 2AD COS α

CDP -trekant

Denne trekanten er rektangel og med sine sider er de trigonometriske årsakene til vinkelen α bygget:

sin α = h/d

cos α = pd/d

Men PD = A - B -siden, derfor:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Du har også:

Tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)

CDB -trekant

I denne trekanten har vi vinkelen hvis toppunkt er i C. Det er ikke merket i figuren, men i begynnelsen skilte det seg ut at det er verdt 180 - α. Denne trekanten er ikke rektangel, så kosinusteorem eller bryststeorem kan påføres.

Nå kan det lett demonstreres at:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Bruke Coseno -teorem:

d₂² = d² + b²- 2dB cos (180 - α) = d² + b²+ 2DB COS α

Eksempler på rektangler

Trapezios og spesielt rektanglene finnes på mange sider, og noen ganger ikke alltid håndgripelige. Her har vi flere eksempler:

Trapecio som et designelement

Geometriske skikkelser florerer i arkitekturen til mange bygninger, for eksempel denne kirken i New York, som viser en struktur i form av rektangel trapesidzoid.

Også den trapesformen er hyppig i utformingen av containere, containere, kniver (Kutter eller nøyaktig), ark og i grafisk design.

Figur 3. Engel inne i et rektangel trapesoid i en kirke i New York. Kilde: David Goehring gjennom Flickr.

Trapezoidal bølgegenerator

Elektriske signaler kan ikke bare være firkantet, sinus eller trekantet. Det er også trapezoidale signaler som er nyttige i mange kretsløp. I figur 4 er det et trapesformet signal sammensatt av to rektangler. Mellom dem danner de en enkelt isosceles trapezoid.

Kan tjene deg: Divisors of 8: Hva er og enkel forklaring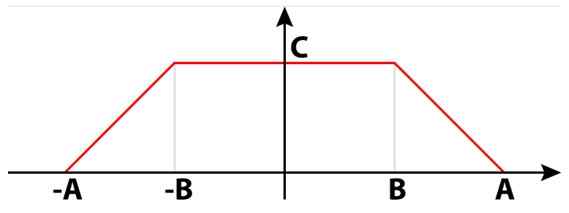

Figur 4. Et trapesoidal signal. Kilde: Wikimedia Commons.

I den numeriske beregningen

For å beregne numerisk den definerte integralen av funksjonen f (x) mellom A og B, brukes trapesregelen for å tilnærme området under grafen til F (x). I den følgende figuren, til venstre.

En bedre tilnærming er den av riktig figur, med flere rektangler.

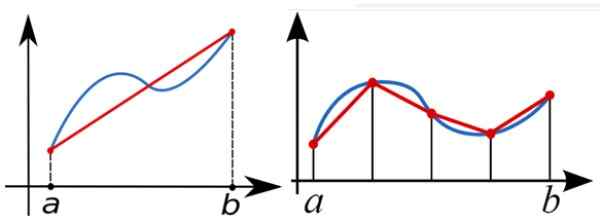Figur 5. Et definert integral mellom A og B er ingenting annet enn området under kurve F (x) mellom disse verdiene. Et trapesformet rektangel kan tjene som den første tilnærmingen til det området, men jo flere trapesoider brukes, jo bedre er tilnærmingen. Kilde: Wikimedia Commons.

Trapezoidal belastningsstråle

Kreftene er ikke alltid konsentrert om et enkelt punkt, siden kroppene de opptrer har betydelige dimensjoner. Slik er tilfellet med en bro som kjøretøy kontinuerlig sirkulerer, vannet på et basseng på de vertikale veggene på det samme eller et tak som vann eller snø akkumuleres.

Det er grunnen til at kreftene er fordelt per enhet med lengde, overflate eller volum, avhengig av kroppen de virker.

Når det gjelder en bjelke, kan en kraft distribuert per lengdeenhet ha forskjellige distribusjoner, for eksempel den av rektangel trapes vist nedenfor:

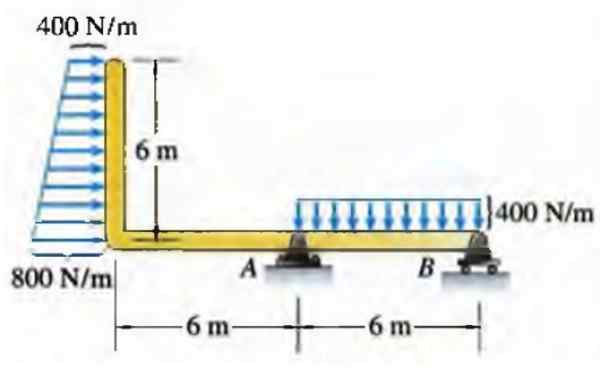Figur 6. Laster på en bjelke. Kilde: Bedford, til. nitten nittiseks. Statisk. Addison Wesley Inter -American.

I virkeligheten tilsvarer ikke alltid distribusjoner vanlige geometriske former som dette, men de kan være en god tilnærming i mange tilfeller.

Som pedagogisk og læringsverktøy

Blokker og laken med geometriske former, inkludert trapesidzoider, er veldig nyttige for barn å gjøre seg kjent med en tidlig alder med den fascinerende verden av geometri.

Figur 7. Blokker med enkle geometriske former. Hvor mange rektangler er skjult i blokkene? Kilde: Wikimedia Commons.

Løste øvelser

- Oppgave 1

I rektangelet trapesoid av figur 1 er den største basen verdt 50 cm og den minste basen er lik 30 cm, er det også kjent at den skrå siden måler 35 cm. Finne:

a) vinkel α

b) høyde

c) Omkrets

d) Medium base

e) område

f) Diagonal

Løsning på

Uttalelsesdataene er oppsummert på denne måten:

A = høyere base = 50 cm

B = mindre base = 30 cm

D = skrå side = 35 cm

Kan tjene deg: grunnleggende operasjoner

For å finne vinkelen α besøker vi formlene og ligningsdelen, for å se hvilken som passer best for dataene som tilbys. Den etterspurte vinkelen finnes i flere av trekantene som er analysert, for eksempel CDP.

Der har vi denne formelen, som inneholder de ukjente og også dataene vi kjenner:

cos α = (a-b) / d

Derfor:

α = buer [(A-B) / D] = buer [(50-30) / 35] = buer 20/35 = 55.15 º

Løsning b

Fra ligningen:

sin α = h/d

h = d.sin α = 35 Sen 55.15 º cm = 28.72 cm

Løsning c

Omkretsen er summen av sidene, og ettersom høyden er lik side C, må vi:

C = h = 28.72 cm

Derfor:

P = (50 + 30 + 35 + 28.72) CM = 143.72 cm

Løsning d

Gjennomsnittlig base er semi -kroppene til basene:

Medium base = (50 + 30 cm)/2 = 40 cm

Løsning e

Trapezoidområdet er:

A = gjennomsnittlig base x høyde = 40 cm x 28.72 = 1148.8 cm².

Løsning f

For diagonal d₁ Denne formelen kan brukes:

d₁² = b² + b² = 2b²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

Og for diagonal d₂:

d₂² = d² + b²+ 2DB COS α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 º = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

Dette er ikke den eneste måten å finne D₂, Siden det også er dab -trekanten.

- Oppgave 2

Følgende hastighetsgraf avhengig av en mobil som har en jevn akselerert rettlinjet bevegelse. Beregn avstanden som ble reist av mobilen i tidsintervallet mellom 0.5 og 1.2 sekunder.

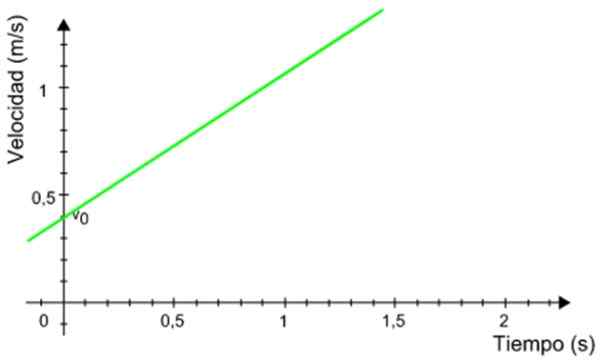Figur 8. Grafisk mot en mobil med ensformelig akselerert gjenkledd bevegelse. Kilde: Wikimedia Commons.

Løsning

Avstanden som er tilbakelagt av mobilen tilsvarer området under grafen, avgrenset av det angitte tidsintervallet.

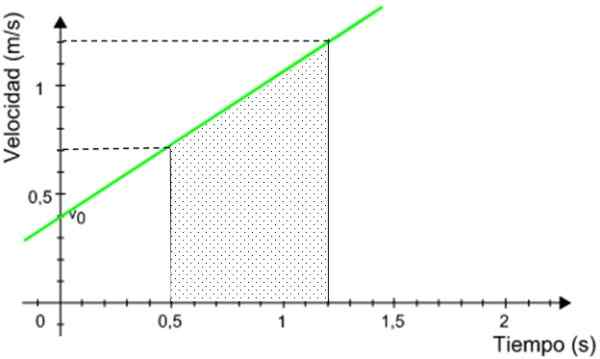Figur 9. Avstanden som er tilbakelagt av mobilen tilsvarer området under grafikken. Kilde: Modifisert av F. Zapata.

Det skyggelagte området er området til et rektangel trapesidzoid, gitt av: