Fysiske baneegenskaper, typer, eksempler og øvelser

De Bane i fysikk Det er kurven som beskriver en mobil når du går gjennom påfølgende punkter under bevegelsen. Siden dette kan ta i bruk utallige varianter, så vil de også være banene som mobilen kan følge.

For å gå fra et sted til et annet, kan en person ta forskjellige stier og forskjellige måter: til fots gjennom fortauene i gater og veier, eller ankomme med bil eller motorsykkel på en motorvei. Under en tur gjennom skogen kan rullatoren følge en komplisert bane som inkluderer svinger, klatring eller slippe opp og til han passerer flere ganger gjennom samme punkt.

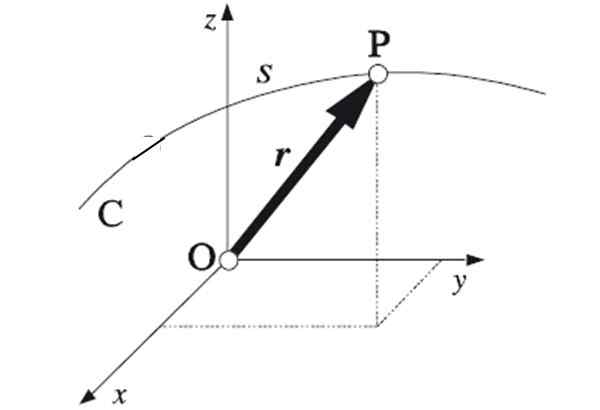Figur 1. Sammen med de ekstreme punktene i hver posisjonsvektor er banen etterfulgt av partikkelen oppnådd. Kilde: Algarabia [Public Domain]

Hvis punktene som mobilen reiser følger en rett linje, vil banen være rettlinjet. Dette er den enkleste banen, for å være en -dimensjonal. Å spesifisere stillingen krever en enkelt koordinat.

Men mobilen kan følge en curvylbane, og kunne lukkes eller åpen. I disse tilfellene krever overvåking av stillingen to eller tre koordinater. Dette er bevegelser i henholdsvis fly og rom. Dette har å gjøre med lenker: Begrensende materielle forhold i bevegelsen. Noen eksempler er:

- Banene som beskriver planetene rundt solen er lukket ellipse -formede bane. Selv om de i noen tilfeller kan tilnærme seg et sirkulært, som for jorden.

- Ballen som keeperen sparker i et målspark følger en parabolsk bane.

- En fugl på flukt beskriver krumlinjede baner i verdensrommet, for i tillegg til å bevege seg på et fly, kan den stige eller lavere nivå etter ønske.

Fysikkbane kan uttrykkes matematisk når mobilposisjon er kjent når som helst. Være r Posisjonsvektoren, som igjen har koordinater x, og og z I det mest generelle tilfellet om en tredimensjonal bevegelse. Å kjenne funksjonen r (T) Banen vil være fullstendig bestemt.

[TOC]

Folkens

Generelt sett kan banen være en ganske komplisert kurve, spesielt hvis du vil uttrykke matematisk. Derfor begynner det med de enkleste modellene, der mobiler reiser på en rett linje eller på et fly, som kan være gulvet eller noe annet egnet:

Bevegelser i en, to og tre dimensjoner

De mest studerte banene er:

- Rettlinjet, Når du reiser på en horisontal, vertikal eller skrå linje. En ball kastet vertikalt oppover denne banen eller en gjenstand som glir nedoverbakke av et skrå fly også. De er en -dimensjonale bevegelser, en enkelt koordinat er nok til å bestemme dens posisjon fullstendig.

- Parabolsk, der mobilen beskriver en parabolabue. Det er hyppig, siden ethvert objekt som er lansert skrått under virkningen av tyngdekraften (et prosjektil) følger denne banen. For å spesifisere mobilposisjonen må du gi to koordinater: x og og.

- Sirkulær, oppstår når den bevegelige partikkelen følger en omkrets. Det er også vanlig i naturen og daglig praksis. Mange hverdagsobjekter følger en sirkulær bane som dekk, maskiner og satellitter i bane, for å gi noen eksempler.

Kan tjene deg: Equipocent Vectors: Definisjon, notasjon, øvelser

- Elliptisk, Objektet beveger seg etter en ellipse. Som nevnt i begynnelsen, er det banen som planetene følger i bane rundt solen.

- Hyperbolsk, Astronomiske gjenstander under handling av en sentral kraft (tyngdekraft), kan følge elliptiske (lukket) eller hyperbolske (åpne) bane, disse er sjeldnere enn den første.

- Spiralformet, o Spiralbevegelse, som en fugl som stiger opp i en termisk strøm.

- Svai eller pendulær, Mobilen beskriver en lysbue i tur / retur -bevegelser.

Eksempler

Banene som er beskrevet i forrige seksjon er veldig nyttige for å raskt få et inntrykk av hvordan bevegelsene til et objekt er. I alle fall er det nødvendig å avklare at banen til en mobil avhenger av observatørens plassering. Dette betyr at den samme hendelsen kan sees på forskjellige måter, etter hvor hver og en er.

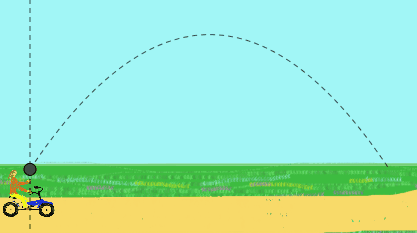
For eksempel en jentepedal med konstant hastighet og kaster en ball opp. Hun observerer at ballen beskriver en rettlinjet bane. 

For en observatør som står på veien som ser det, vil ballen imidlertid ha en parabolsk bevegelse. For ham ble ballen opprinnelig kastet med en skrå hastighet, resultatet av hastigheten opp av jentas hånd pluss sykkelhastigheten.

Figur 2. Denne animasjonen viser den vertikale lanseringen av en ball laget av en jente som går på sykkel, som hun ser (rettlinjet bane) og som du ser en observatør (parabolsk bane). (Utarbeidet av f. Zapata).

Bane for en mobil på en eksplisitt, implisitt og parametrisk måte

- Eksplisitt, direkte spesifisere kurven eller geometrisk sted gitt av ligningen og (x)

- Implisitt, der en kurve uttrykkes som f (x, y, z) = 0

-Parametrisk, På denne måten oppstår x- og y z -koordinatene avhengig av en parameter som generelt er valgt som tid t. I dette tilfellet består banen av funksjonene: x (t), og T) og z (t).

Deretter er to veldig studerte baner detaljert i filmatikken: den parabolske banen og den sirkulære banen.

Lansering i et vakuum

Et objekt (prosjektilet) kastes og danner en vinkel A med horisontalt og med en innledende hastighet v_enten Som bildet viser. Luftmotstand tas ikke i betraktning. Bevegelsen kan behandles som to uavhengige og samtidige bevegelser: en horisontal med konstant og en annen vertikal hastighet under virkningen av tyngdekraften.

x (t) = x_enten +v_okse.t

og (t) = y_enten +v_Oy.T -½g.t²

Disse ligningene er Parametriske ligninger av prosjektillanseringen. Som forklart ovenfor har de felles parameter t, hva er tid.

I høyre trekant av figuren kan følgende sees:

v_okse = v_enten cos θ_Yo

v_Oy = v_enten sin θ_Yo

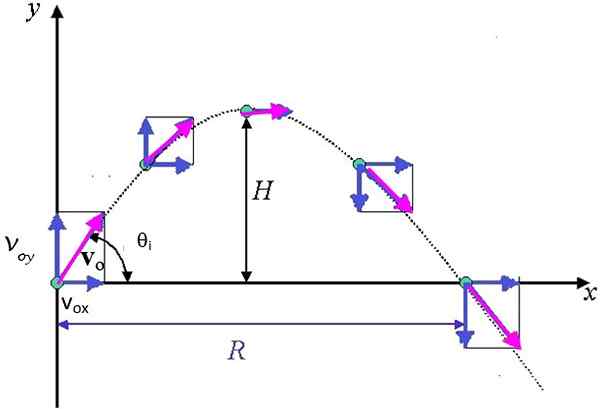Figur 3. Parabolsk bane etterfulgt av et prosjektil, som viser komponentene i hastighetsvektoren. H er maksimal og R -høyden er den maksimale horisontale rekkevidden. Kilde: AYUSH12GUPTA [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)]

Ved å erstatte disse ligningene som inneholder lanseringsvinkelen i de parametriske ligningene er det:

Kan tjene deg: Diffraksjon av lyd: Hva er, eksempler, applikasjoner

x (t) = x_enten +v_enten cos θ_Yo.t

og (t) = y_enten +v_enten. sin θ_Yo.T -½g.t²

Parabolsk bane ligning

Den eksplisitte ligningen av banen er å rydde t for ligningen for x (t) og erstatte i y (t) ligningen (t). For å lette algebraisk arbeid, kan det antas at opprinnelsen (0,0) er på lanseringspunktet og på denne måten x_enten = y_enten = 0.

Etter å ha forenklet parameteren "t”Det er eliminert og ligningen som gjenstår er og avhengig av x: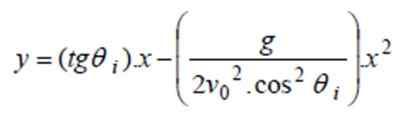

Dette er bane -ligningen i Eksplisitt form.

Sirkulær bane

En sirkulær bane er gitt av:

(X - x_enten)² + (og - og_enten)² = R²

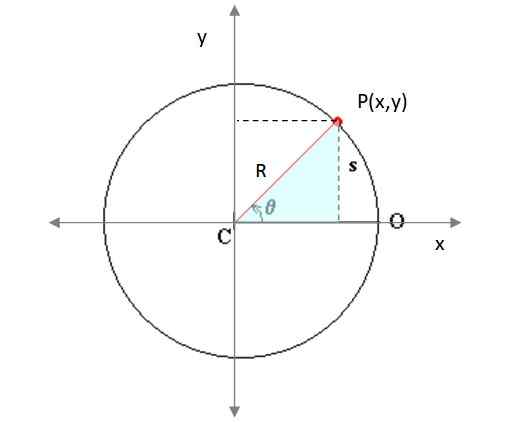Figur 4. En partikkel beveger seg i en sirkulær bane på flyet. Kilde: Modifisert av F. Wikimedia Commons sko.

Her x_enten og og_enten De representerer sentrum av omkretsen beskrevet av mobilen og R er radien til den samme. P (x, y) er et poeng av banen. Fra den skyggelagte rektangeletrekanten (figur 3) blir det advart om:

x = r. cos θ

y = r. sin θ

Parameteren er i dette tilfellet feievinkelen θ, kalt vinkelforskyvning. I det spesielle tilfellet at vinkelhastigheten ω (vinkel feid per tidsenhet) er konstant, kan det bekreftes at:

θ = θ_enten + Ωt

Hvor θ_enten Det er den første vinkelposisjonen til partikkelen, som hvis den blir tatt som 0, reduseres til:

θ = ωt

I dette tilfellet vender tiden tilbake til parametriske ligninger som:

x = r.cos ωt

y = r. sin ωt

Enhetsvektorene Yo og J De er veldig praktisk å skrive posisjonsfunksjonen til et objekt r (T). De indikerer instruksjonene på aksen x og på aksen og henholdsvis. I sine vilkår er plasseringen av en partikkel som beskriver en ensartet sirkulær bevegelse:

r (t) = r.cos ωt Yo + R. sin ωt J

Løste øvelser

Trening løst 1

En kanon kan skyte en kule med en hastighet på 200 m/s og en vinkel på 40º med hensyn til horisontalen. Hvis lanseringen utføres i flatt terreng og luftmotstanden blir foraktet, finn:

a) bane -ligningen og (x) ..

b) De parametriske ligningene x (t) og og T).

c) den horisontale rekkevidden og tiden som prosjektilet varer i luften.

d) Høyden som prosjektilet ligger når x = 12.000 m

Løsning på)

a) For å finne banen, erstattes verdiene som er gitt i ligningen y (x) for den foregående delen:

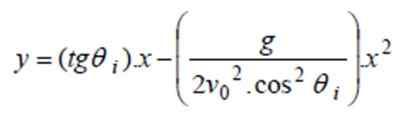
og (x) = tg 40º. x - 9.8/(2 '400². Cos²40º) x² ⇒  og (x) = 0.8391 x - 0.0000522X²

Løsning B)

b) Lanseringspunktet er valgt ved opprinnelsen til koordinatsystemet (0,0):

x (t) = x_enten +v_okse.T = 400'Cos 40º.T = 306.42. t.

og (t) = y_enten +v_Oy.T -½g.t²= 400 'Sen 40º.T - 0.5 '9.8'T²= 257.12 T - 4.9.t²

Løsning C)

c) For å finne tiden som prosjektilet varer i luften, er det gjort og (t) = 0, Å være lanseringen er laget i flatt terreng:

Kan tjene deg: det som er relativt og absolutt ruhet?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 s = 52.473 s

Det horisontale maksimale omfanget erstatter denne verdien i x (t):

x_Maks = 306.42'52.47 m = 16077.7 m

En annen måte å finne x_Maks Det gjør direkte y = 0 i bane -ligningen:

0 = 0.8391 x_Maks - 0.0000522 x²_Maks

x = 0.8391 /0.0000522 M = 16078.5m

Det er en liten forskjell på grunn av avrunding av desimaler.

D) Løsning

d) For å kjenne høyden når x = 12000 m denne verdien erstattes direkte i bane -ligningen:

og (12000) = 0.8391'12000 - 0.000052212000² M = 2552.4 m

Trening løst 2

Posisjonsfunksjonen til et objekt er gitt av:

r (t) = 3t Yo + (4 -5t²) J m

Finne:

a) Ligningen for banen. Hva kurve er?

b) startposisjonen og posisjonen når t = 2 s.

c) Forskyvningen gjort etter t = 2 s.

Løsning

a) Posisjonsfunksjonen er gitt i form av enhetsvektorene Yo og J, som bestemmer adressen på aksene x og og, derfor:

x (t) = 3t

og T) = 4 -5t²

Bane -ligningen og (x) Han rydder t av x (t) og erstatte inn og T):

T = x/3

og (x) = 4 -5. (x/3)² = 4 - 5x²/9 (lignelse)

b) startposisjonen er: r (2) = 4 J m ; Stillingen i T = 2 s er r (2) = 6 Yo -16 J m

c) Forskyvning Dr Det er subtraksjon av de to posisjonsvektorene:

Δr = r (2) - r (2) = 6 Yo -16 J- 4 J = 6 Yo - tjue J m

Trening løst 3

Jorden har en radius r = 6300 km, og det er kjent at rotasjonsperioden av bevegelsen rundt sin akse er en dag. Finne:

a) Ligningen av banen til et punkt på jordoverflaten og dens posisjonsfunksjon.

b) Hastigheten og akselerasjonen av nevnte punkt.

Løsning på)

a) Posisjonsfunksjonen for et hvilket som helst punkt i sirkulær bane er:

r (t) = r.cos ωt Yo + R.sin ωt J

Du har jordens radius R, men ikke vinkelhastigheten ω, men den kan beregnes fra perioden, og vet at for den sirkulære bevegelsen er det gyldig å si at:

Ω = 2π × Frekvens = 2π / periode

Bevegelsesperioden er: 1 dag = 24 timer = 1440 minutter = 86400 sekunder, derfor:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Erstatte i posisjonsfunksjonen:

r (t) = r.cos ωt Yo + R. sin ωt J = 6300 (cos 0.000023148T Yo + sin 0.000023148T J) Km

Stien i en parametrisk form er:

x (t) = 6300. cos 0.000023148T

og (t) = 6300. sin 0.000023148T

Løsning B)

b) For den sirkulære bevegelsen, størrelsen på den lineære hastigheten v av et punkt er relatert til vinkelhastighet W gjennom:

v = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Til og med å være en konstant bevegelse av 145.8 m/s, Det er en akselerasjon som peker på sentrum av den sirkulære bane, ansvarlig for å holde poenget i rotasjon. Det er centripetal akselerasjon til_c, gitt av:

til_c = v² / R = (145.8 m/s)² / 6300 × 10³ m = 0.00337 m/s².

Referanser

1. Giancoli, d. Fysikk. (2006). Prinsipper med applikasjoner. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 23 - 27.
3. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 21-22.
4. Rex, a. (2011). Fundamentals of Physics. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Universitetsfysikk med moderne fysikk. 14^th. Ed. Volum1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7^ma. Utgave. Mexico. Cengage Learning Editors. 23-25.
7. Serway, r., Vulle, c. (2011). Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
8. Wilson, J. (2011). Fysikk 10. Pearson Education. 133 - 149.