Likebent trekant

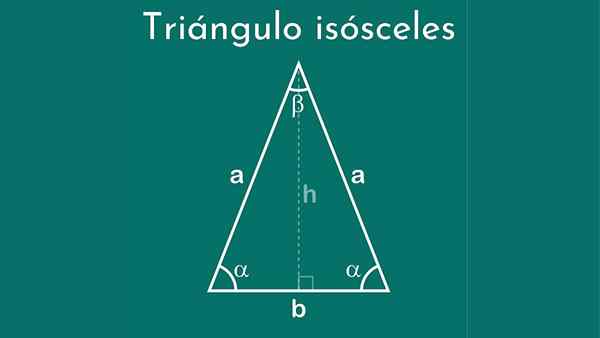
Isosceles -trekanten har to like sider og en annen

Hva er en isosceles -trekant?

EN likebent trekant Det er en tre -sidig polygon, der to av dem har samme tiltak og tredje side et annet tiltak. Denne siste siden kalles base. På grunn av denne karakteristikken ble dette navnet gitt, som på gresk betyr "like ben".

Trekanter er polygoner betraktet som de enkleste i geometri, fordi de er dannet av tre sider, tre vinkler og tre hjørner. Det er de som har minst antall sider og vinkler med hensyn til de andre polygonene, men bruken deres er veldig omfattende.

Kjennetegn på isosceles -trekanter

Isosceles -trekanten ble klassifisert ved hjelp av målene på sidene som en parameter, siden to av sidene er kongruente, det vil si at de har samme lengde.

I henhold til amplituden til de indre vinklene, er isosceles -trekantene klassifisert som:

• Isosceles Rectangle Triangle: To av sidene er de samme. Et av vinklene er rette (90^enten) Og de andre er de samme (45^enten Hver)
• Isosceles stump Triangle: To av sidene er de samme. Et av vinklene er stump (> 90^enten).
• Isosceles acutangle trekant: To av sidene er de samme. Alle dens vinkler er akutte (< 90^enten), Der to har samme mål.

Komponenter

• Medianen: Det er en linje som forlater fra midtpunktet på den ene siden og når motsatt toppunkt. De tre mediene deltar på et punkt som heter baricentro eller centroid.
• Bisektoren: Det er en semi -rett som deler vinkelen til hvert toppunkt i to vinkler med like mål. Det er grunnen til at det er kjent som symmetriakse, og denne typen trekanter har bare en.
• MediaTrix: Det er et segment vinkelrett på siden av trekanten, som har sin opprinnelse midt i dette. Det er tre meklinger i en trekant og deltar på et poeng som heter Circumentro.
• Høyden: Det er linjen som går fra toppunktet til siden som er motsatt, og også denne linjen er vinkelrett på den siden. Alle trekanter har tre høyder, som sammenfaller på et punkt som heter Ortocenter.

Isosceles trekanter egenskaper

Isosceles -trekanter er definert eller identifisert fordi de har flere egenskaper som representerer dem, stammer fra teoremene foreslått av store matematikere:

Interne vinkler

Summen av interne vinkler er alltid lik 180^enten.

Sum av sidene

Summen av tiltakene på to sider skal alltid være større enn målet på tredje side, a + b> c.

Kongruente sider

Isosceles -trekanter har to sider med samme mål eller lengde; det vil si at de er kongruente, og den tredje siden er forskjellig fra disse.

Kongruente vinkler

Isosceles -trekanter er også kjent som isoanguløse trekanter, fordi de har to vinkler som har samme mål (kongruent). Disse ligger ved basen av trekanten, i motsetning til sidene som har samme lengde.

Kan tjene deg: trapesoidal prisme

På grunn av dette er teoremet som fastslår det:

"Hvis en trekant har to kongruente sider, vil vinklene i motsetning til disse sidene også være kongruente". Derfor, hvis en trekant er isosceles, er vinklene på basene kongruente.

Eksempel:

I den følgende figur observeres en ABC -trekant. Når du tegner bisektoren fra toppunktet av vinkel B til basen, er trekanten delt inn i to BDA- og BDC -trekanter:

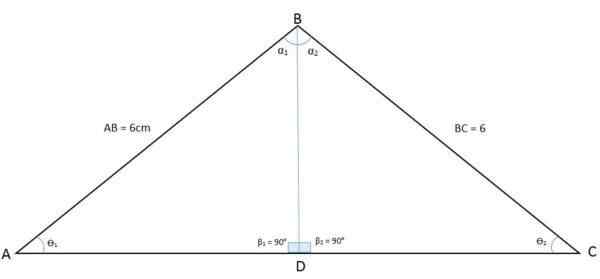Bisektor som deler seg inn i to trekanter lik Isosceles -trekanten

På denne måten ble også vinkelen til toppunkt B delt i to like vinkler. Bisektoren er nå den vanlige siden (BD) mellom de to nye trekantene, mens sidene AB og BC er de kongruente sidene. Dette er tilfelle av side, vinkel, side (Lal).

Det viser at vinklene til toppunktene A og C har samme mål, så godt det kan påvises at når BDA- og BDC -trekantene er kongruente, er AD- og DC -sidene også.

Høyde, median, mediatrix og bisektor er tilfeldig

Linjen trukket fra toppunktet motsatt av basen til midtpunktet til Isosceles Triangle Base, er samtidig høyden, medianen og mediatrix, så vel som bisektoren i forhold til den motsatte vinkelen på basen.

Alle disse segmentene sammenfaller i et som representerer dem.

Eksempel:

I den følgende figur observeres ABC -trekanten med et middels m punkt som deler basen i to BM- og CM -segmenter.

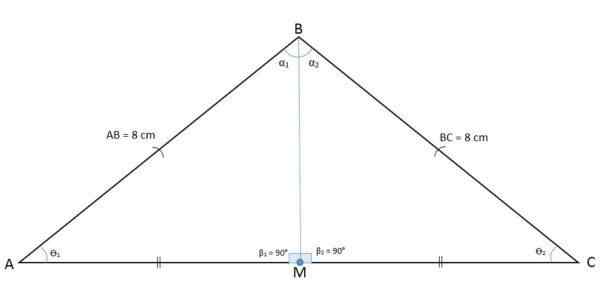Høyde, median, mediatrix og bisektor er tilfeldig

Når du tegner et segment fra punkt M til motsatt toppunkt, oppnås median AM per definisjon, noe som er relativt til toppunkt A og til BC -siden.

Når AM -segmentet deler ABC -trekanten i to like trekanter AMB og AMC, betyr det at tilfellet med side, vinkel, side, og derfor AM også vil være bisektor for Bâc.

Det er grunnen til at bisektoren alltid vil være lik median og omvendt.

AM -segmentet danner vinkler som har samme mål for AMB- og AMC -trekanter; Det vil si at de er supplerende, slik at målet for hver enkelt vil være:

Med. (AMB) + Med. (AMC) = 180^enten

2 _* Med. (AMC) = 180^enten

Med. (AMC) = 180^enten ÷ 2

Med. (AMC) = 90^enten

Det kan være kjent at vinklene dannet av AM -segmentet angående trekanten er rette, noe som indikerer at dette segmentet er helt vinkelrett på basen.

Derfor representerer den høyden og mediatrix, og vet at M er midtpunktet.

Derfor er linjen AM:

• Representerer høyden på BC.
• Er middels størrelse.
• Det er inneholdt i BC MediaTrix.
• Det er bisektoren til toppunktvinkelen â

Relative høyder

Høydene som er relativt til likesidene har samme tiltak også.

Kan tjene deg: perfekte tall: hvordan identifisere dem og eksempler

Ettersom Isosceles -trekanten har to like sider, vil de to respektive høydene også være de samme.

Orocentro, Baricentro, Incentro og Colecentro Coinsides

Ettersom høyden, median, bisektor og mediatrix relatert til basen er representert samtidig av det samme segmentet, vil ortosenteret, Baricentro, Incentre og Circumentro være Colineal -punkter, det vil si at de vil bli funnet på samme linje:

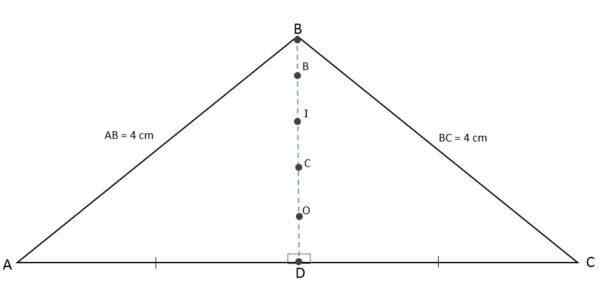Ortocenter, baricentro, incentro og circumcentro er også tilfeldig

Isosceles Triangles Beregning

Hvordan beregne omkretsen?

Omkretsen til en polygon beregnes av summen av sidene.

Som i dette tilfellet Isosceles -trekanten har to sider med samme mål, beregnes omkretsen med følgende formel:

P = 2_*(Side A) + (Side B).

Hvordan beregne høyden?

Høyden er linjen vinkelrett på basen, deler trekanten i to deler lik ved å utvide til motsatt toppunkt.

Høyden representerer motsatt kateto (a), halvparten av basen (b/2) til den tilstøtende kateto og "A" -siden representerer hypotenusen.

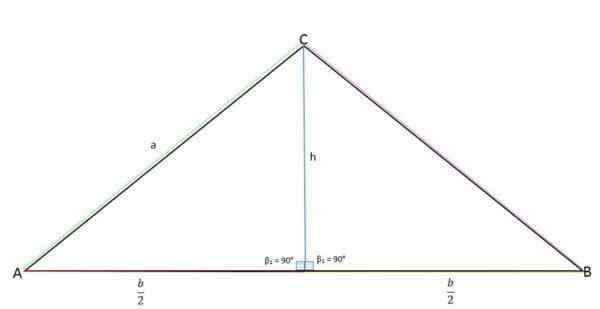Beregning av høyden på en isosceles -trekant

Ved hjelp av Pythagoras -teoremet kan verdien av høyden bestemmes:

til² + b² = c²

Hvor:

til² = høyde (h).

b² = B / 2.

c² = side a.

Bytte ut disse verdiene i Pythagoras -teoremet, og rydde høyden du har:

h² + (b / 2)² = til²

h² + b² / 4 = til²

h² = til² - b² / 4

H = √ (til² - b² / 4).

Hvis vinkelen dannet av de kongruente sider er kjent, kan høyden beregnes med følgende formel:

Hvordan beregne området?

Trekantene beregnes alltid med samme formel, multipliserer basen med høyde og deling med 2:

Det er tilfeller der bare tiltakene på to sider av trekanten er kjent og vinkelen som dannes mellom dem. I dette tilfellet, for å bestemme området er det nødvendig å anvende de trigonometriske grunnene:

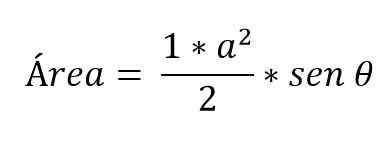
Hvordan beregne trekantbasen?

Ettersom isosceles -trekanten har to like sider, for å bestemme verdien av basen er det nødvendig å vite i det minste målet på høyden eller en av dens vinkler.

Når du kjenner høyden, brukes Pythagoras teorem:

til² + b² = c²

Hvor:

til² = høyde (h).

c² = side a.

b² = B / 2, er ukjent.

Vi fjerner b² av formelen og vi må:

b² = a² - c²

B = √ a² - c²

Siden denne verdien tilsvarer halvparten av basen, må den multipliseres med 2 for å oppnå det komplette målet av Isosceles Triangle Base:

B = 2 _* (√ a² - c²)

I tilfelle at bare verdien av dens like sider og vinkelen mellom dem er kjent, brukes trigonometrien, og trekker en linje fra toppunktet til basen som deler isosceles -trekanten i to rektangler trekanter.

På denne måten beregnes halvparten av basen med:

Verdien av høyden og vinkelen på toppunktet som er imot basen er også kjent. I så fall kan av trigonometri basen bestemmes:

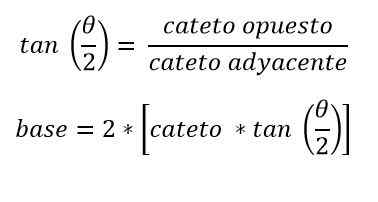
Øvelser

Første trening

Finn Isosceles ABC -trekantområdet, vel vitende om at to av sidene måler 10 cm og den tredje siden måler 12 cm.

Det kan tjene deg: Antiderivat: Formler og ligninger, eksempler, øvelser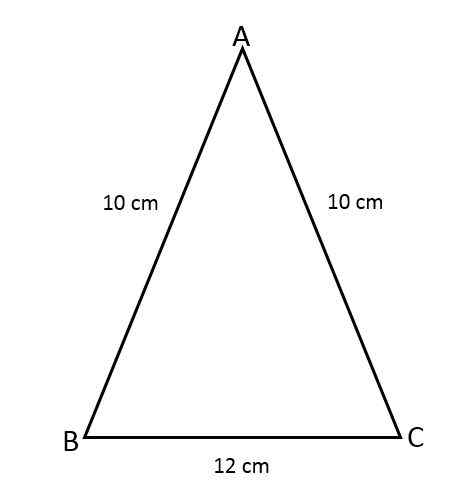

Løsning

For å finne trekantområdet, er det nødvendig.

Følgende Isosceles Triangle -data er tilgjengelige:

• Like sider (a) = 10 cm.
• Base (b) = 12 cm.

Verdiene erstattes i formelen:

Andre trening

Lengden på de to like sidene av en isosceles -trekant måler 42 cm, foreningen av disse sidene danner en vinkel på 130^enten. Bestem verdien av tredje side, området for den trekanten og omkretsen.

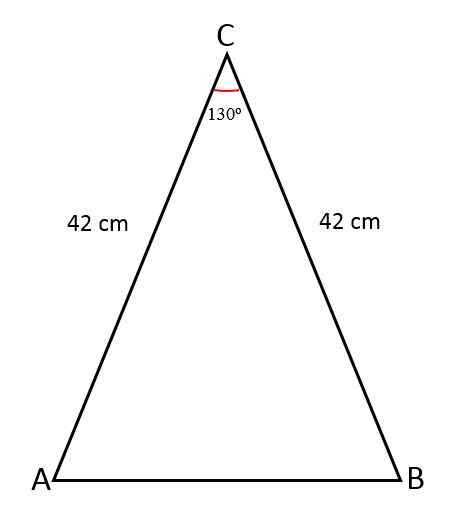
Løsning

I dette tilfellet er målene og vinkelen kjent mellom disse.

For å kjenne verdien på den manglende siden, det vil si basen av den trekanten, en linje vinkelrett på den er tegnet, og deler vinkelen i to like deler, en for hvert rektangeletrekant som dannes.

• Like sider (a) = 42 cm.
• Vinkel (ɵ) = 130^enten

Nå, ved trigonometri, beregnes verdien av halvparten av basen, noe som tilsvarer halvparten av hypotenusen:

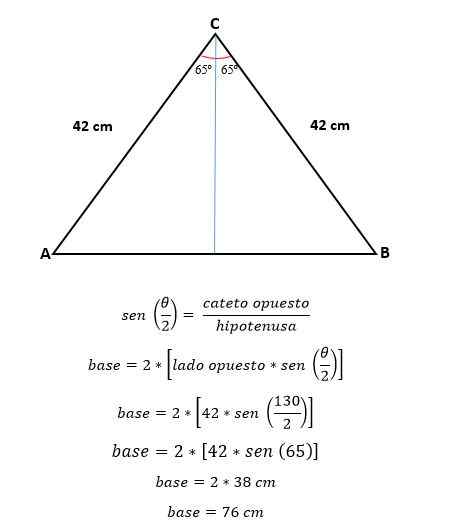
For å beregne området er det nødvendig å vite høyden på den trekanten, som kan beregnes med trigonometri eller av Pythagoras -teoremet, nå som verdien på basen allerede var bestemt.

Av trigonometri vil være:

Omkretsen beregnes:

P = 2_*(Side A) + (Side B).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Tredje øvelse

Beregn de indre vinklene til Isosceles -trekanten, vel vitende om at grunnvinkelen er  = 55^enten

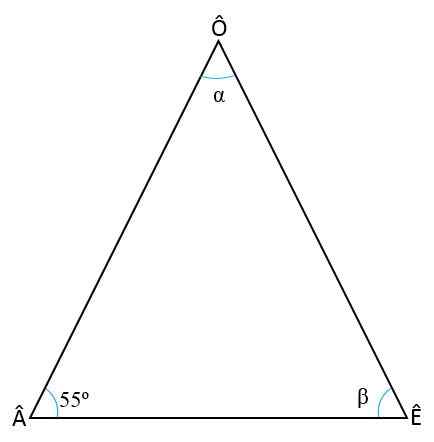
Løsning

For å finne de to manglende vinklene (ê og ô) er det nødvendig å huske to egenskaper til trekantene:

• Summen av de indre vinklene til hver trekant vil alltid være = 180^enten:

 + ê + ô = 180 ^enten

• I en isosceles -trekant er vinklene på basen alltid kongruente, det vil si at de har samme tiltak, derfor:

 = ô

Ê = 55^enten

For å bestemme verdien av vinkelen ê blir verdiene til de andre vinklene i den første regelen erstattet og ê blir fjernet:

55^enten + 55^enten + Ô = 180 ^enten

110 ^enten + Ô = 180 ^enten

Ô = 180 ^enten - 110 ^enten

Ô = 70 ^enten.

Referanser

1. Álvarez, e. (2003). Geometrielementer: med mange øvelser og kompassgeometri. University of Medellin.
2. Álvaro Rendón, til. R. (2004). Teknisk tegning: Aktivitetsnotatbok.
3. Angel, a. R. (2007). Elementær algebra. Pearson Education.
4. Arthur Goodman, L. H. ( nitten nittiseks). Algebra og trigonometri med analytisk geometri. Pearson Education.
5. Baldor, a. (1941). Algebra. Havana: kultur.
6. José Jiménez, L. J. (2006). Matematikk 2.
7. Tuma, J. (1998). Engineering Mathematics Handbook. Wolfram Mathworld.