Stump trekant

Vi forklarer hva en stump trekant er, dens elementer, egenskaper, typer, eksempler og en løst øvelse

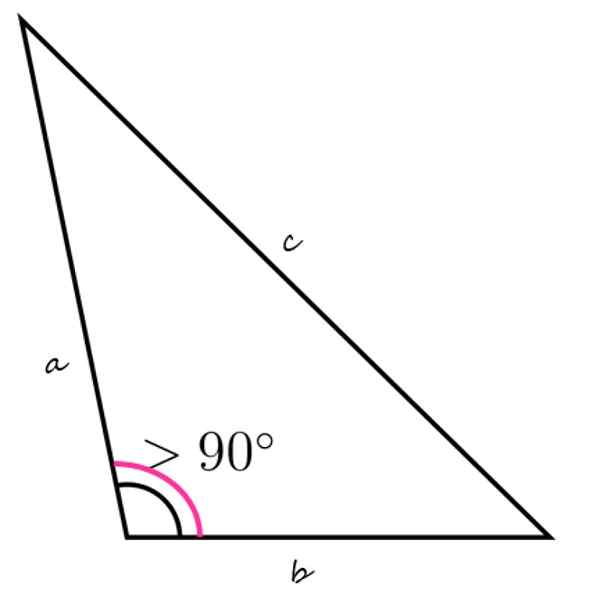Den stumpe trekanten er preget av å ha en indre vinkel større enn 90º

Hva er en stump trekant?

EN stump trekant Det er den flate figuren, lukket og med tre sider, som også inneholder en stump innvendig vinkel, det vil si større enn 90º og mindre enn 180º.

Enhver trekant inneholder 3 indre vinkler, og hvis en av dem er stump, er de to andre, med makt, akutt, fordi summen av de indre vinklene til en hvilken som helst trekant, alltid er lik 180º.

Toppfiguren viser et eksempel på en stump trekant, med den nedre venstre indre vinkelen større enn 90º. De gjenværende indre vinklene må legge til mindre enn 90 º, bare på denne måten er det sant at summen av de tre er lik 180º.

I tillegg til de stumpe trekantene, er det akutanguløse trekanter, hvis alle dens indre vinkler er akutte, og rektangel -trekanter, når en av de indre vinklene måler nøyaktig 90º.

Elementer av de stumpe trekantene

Obtusángulos -trekanter har de vanlige elementene til alle trekanter: de er 3 -sidede flate figurer, med 3 interne vinkler og 3 hjørner. I tillegg har de bemerkelsesverdige segmenter, kalt Cevians, som høyde, median og mediatrix, og punkter der Cevians krysser hverandre.

Hvert av disse elementene er kort definert som følger:

-Sider, er segmentene som utgjør figuren.

-Hjørner, Krysspunkter for hvert par tilstøtende sider.

-Interne vinkler, De er mellom to tilstøtende sider, på den indre siden av figuren, sammenfallende toppunktet i vinkelen med den for trekanten.

-Eksterne vinkler, De er mellom den ene siden og forlengelsen av den tilstøtende siden, utenfor figuren, toppunktet er vanlig, både av trekanten og vinkelen. Summen av målet mellom den indre vinkelen og dens ytre tilstøtende vinkel er 180º, slik at de er komplementære vinkler.

Det kan tjene deg: Tukey Test: Det som er i tilfelle av eksempel løst trening

-Høyde, Det er målet på det vinkelrettsegmentet som blir med i et toppunkt med motsatt side, eller med utvidelsen av dette.

-Median, linje som er rettet fra et toppunkt til midten av motsatt side.

-Mediatrix, segment vinkelrett på siden og det passerer bare gjennom sentrum.

-Bisektor, Det er et segment som deler seg i en halv indre vinkel på trekanten.

-Orocentro, Krysspunktet for de tre høydene.

-Barycenter, Også kalt centroid, det er poenget hvor de tre medianene krysser hverandre.

-Circumcentro, Her er de tre mediatriser kuttet.

-Incenter, Konfluenspunkt for bisektorer.

Når disse konseptene er gjennomgått, er noen av de mest bemerkelsesverdige egenskapene til de stumpe trekantene beskrevet nedenfor.

Kjennetegn

1.- Summen av de tre indre vinklene til den stumpe trekanten er 180º, derfor kan bare en av dens indre vinkler være større enn 90º, mens summen av de resterende to er mindre enn 90º.

2.- Den lengste siden av den stumpe trekanten er imot den stump vinkelen.

3.- I en stump trekant, krysser høydene fra toppunktene som lager akutt vinkel, utvidelsene av motsatte sider.

4.- Ortosenteret til en stump trekant er ute av figuren.

5.- Omkretsten av den stumpe trekanten faller også ut av trekanten (dette skjer ikke med acutangle -trekanten).

6.- Det er bare mulig å registrere en firkant i den stumpe trekanten, og støtter en av sidene på torget på den lengste siden av trekanten. To firkanter kan tegnes, og støtter siden på de korteste sidene av trekanten, og etterlater et toppunkt ikke registrert (som ikke berører siden av trekanten).

Kan tjene deg: Tidecágono

7.- Være en stump trekant av sider (a, b, c), å være den lengste siden. Følgende ulikhet er gyldig:

til²+b² < c²

8.- De er to stumpe trekanter, hvis respektive sider er (a, b, c) og (u, v, w). De lengste sidene av hver er C og W, så følgende ulikhet er oppfylt:

A ∙ U + B ∙ V < c∙w

Typer hindrende trekanter

De stumpe trekantene kan være av to typer, i henhold til lengden på sidene:

• Likebent
• Scalene

De er kort beskrevet nedenfor:

Likebent trekant

Det er en som har to like sider og en annen, det vil si at sidene er (a, a, c).

Når Isosceles -trekanten begge er stump, er sider av målet “A” kortere og “C” -siden er den lengste. Den stumpe vinkelen dannes mellom de samme sidene, mens de to akutte vinklene har like mål og dannes mellom sider "A" og siden "C".

Og som det fremgår av foregående avsnitt, side "C", fordi det er den lengste, er det imot den stump vinkelen.

Scalene Triangle

De tre sidene av Scalene Triangle har forskjellige mål: (a, b, c).

Eksempler

Eksempel 1

Trekanten vist i følgende figur er stump. Den stumpe vinkelen er γ = 114.5. og det er bekreftet at summen av de tre indre vinklene er 180º:

114.5. + 36.8º + 28.6. ≈ 180º

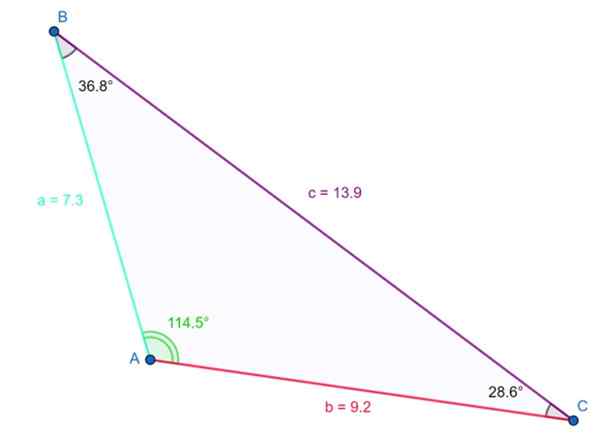Eksempel på stump trekant. Kilde: f. Zapata

Den lengste siden måler 13.9 enheter og er imot den stumpe vinkelen. Den nevnte ulikheten er også oppfylt:

til²+b² < c²

Kan tjene deg: proporsjonalitetsrelasjoner: konsept, eksempler og øvelser

Ja A = 7.3 og B = 9.2, da:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Eksempel 2

I Calabi -trekanten er det mulig å plassere det største mulige firkanten, på tre forskjellige måter innenfor trekanten, som vist i følgende figur.

Calabis trekant er isosceles og stødig. Den stumpe vinkelen er omtrent 101.736 ° og akutte vinkler ved basen måler begge 39.13., også omtrent.

Trening løst

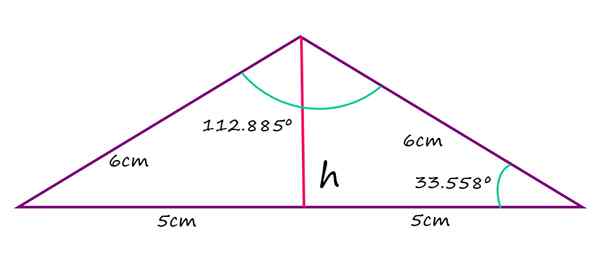
Like sidene av en stump isosceles -trekantmål 6 cm, mens den lengste siden måler 10 cm. Beregn verdien av den stumpe vinkelen, den for de gjenværende agudosvinklene og høyden fra nevnte toppunkt til basen.

Løsning

Kosinosteoremet kan brukes til å finne kosinus i den stumpe vinkelen. Deretter, ved hjelp av kalkulatoren, bestemmes den aktuelle vinkelen, betegnet som γ.

Cosenos teorem uttaler at:

c² = a² +b² - 2ab ∙ cos γ

Der γ er vinkelen mellom sidene A og B. Siden trekanten er isosceles, er sidene A og B de samme, derfor:

c² = 2a² - 2²∙ cos γ

Rydde cos γ:

 Den stumpe vinkelen er -0 kosinusbuen.38889, som er omtrent 112.885º. Verdien av α, den akutte vinkelen dannet av 6 cm sidene med 10 cm er:

2a + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Isosceles stump Triangle. Kilde: f. Zapata

Når det. I et slikt tilfelle gjelder Pythagoras -teoremet for direkte å finne verdien av H: