Kjennetegn skrå trekanter, eksempler, øvelser

De Skrå trekanter De er de som ikke har rett vinkel, derfor er ingen av deres indre vinkler lik 90º. Så en skrå trekant kan være Akutangel eller stump.

I det første tilfellet er trekantens indre vinkler akutte eller hva som er det samme: mindre enn 90º, mens det i det andre er alltid en vinkel større enn 90 º, det vil si en stump vinkel. La oss se på et eksempel på hver i følgende figur:

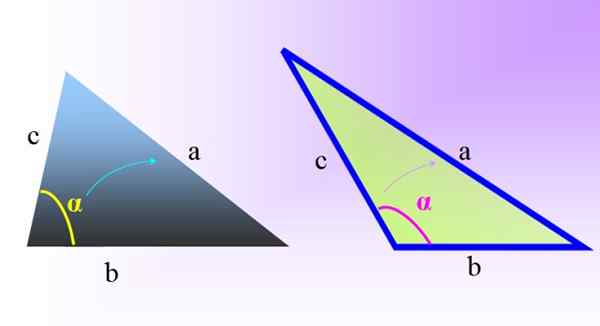Figur 1. Skrå trekanter: til venstre for en skrå og acutangle -trekant. Til høyre en skrå og stump trekant. Kilde: f. Zapata.

For å finne lengdene på sidene og målingene av de indre vinklene til denne typen trekanter, er det ikke mulig å bruke Pythagoras teorem i mangel av rette vinkler.

Imidlertid er det alternativer for å løse trekanten: teoremene til kosinus og barm og det faktum at summen av de indre vinklene er lik 180º.

[TOC]

Oblicuágulos trekanter eksempler

Veiledende oss i figur 1, kan vi lett gjenkjenne de skrå trekantene gjennom to kriterier som vi vil gi nedenfor.

Acutangle Triangle

Være trekanten på sidene A, B og C, med α vinkelen foran siden til.

Hvis kvadratet på siden motsatt av den akutte vinkelen α, er mindre enn summen av rutene på de gjenværende sidene, er trekanten akuttanglet. Algebraisk:

til² < b² + c²; α < 90º

Den relative likesidlige trekanten, den som har sine tre sider av samme mål, er akuttangrep og derfor skrå, siden dens indre vinkler er like og måler 60º.

Stump trekant

På den annen side, hvis torget på motsatt side til Ved stump vinkel α er større enn summen av rutene til de to andre, vi er i nærvær av en stump trekant. Derfor:

til² > b² + c²; α> 90º

For eksempel er en trekant hvis indre vinkler er 105 º, 60º og 15º en stump skrå trekant. Merk at 105º + 60º + 15º = 180º.

Teoremer om bihule og kosinus

For å løse de skrå trekantene, det vil si å finne tiltakene fra alle sidene og alle deres vinkler, er teoremene til brystet og kosinuset påkrevd.

La A, B og C sidene av en trekant, og α, β og γ deres indre vinkler. Så:

Bryststeorem

Bryststeoremet etablerer følgende:

Der α er den motsatte vinkelen til side A, er β vinkelen i motsetning til side B og γ er vinkelen foran side C.

Det kan tjene deg: Antiderivat: Formler og ligninger, eksempler, øvelser

Tilsvarende:

Vi velger å bruke bryststeoremet når vi skal løse en trekant enn flere vinkler er kjent enn sider.

Coseno teorem

I følge Coseno -teorem:

c² = a² + b² - 2⋅a⋅b⋅cos γ

Igjen er vinkelen γ foran side C. Vi kan også skrive tilsvarende uttrykk for sider A og B, som følger:

til² = b² + c² - 2⋅B⋅C⋅COS α

OG

b² = a² + c² - 2⋅a⋅c⋅cos β

Kosinusteoremet brukes helst når verdien av to sider og vinkelen mellom dem er kjent. Når de tre sidene av en trekant har vært kjent, lar teoremet oss beregne kosinus i vinkelen mellom to av dem.

Løste øvelser

- Oppgave 1

Sjekk at trekanten hvis sider måler 20, 10 og 12 vilkårlige enheter er stump.

Løsning

Vi kjenner ikke noen av de indre vinklene, men i henhold til kriteriene som tjener til å gjenkjenne stumpe trekanter, kan vi heve ulikheter med sidene på sidene for å observere om det er oppfylt.

Først finner vi rutene på hver side:

tjue² = 400

10² = 100

12² = 144

Og vi ser det faktisk: 400> 100 + 144, siden 400> 244. Derfor inneholder trekanten en vinkel større enn 90 º, som ligger foran siden som måler 20. Følgelig er denne trekanten, i tillegg til å være skrå, også stump.

- Oppgave 2

Gitt den skrå trekanten vist i figur 2, hvis tiltak er gitt i vilkårlige enheter, bestem:

a) Verdien på x. Er det et akutangrep eller stump trekant?

b) De gjenværende indre vinklene til trekanten

c) Omkrets

d) område.

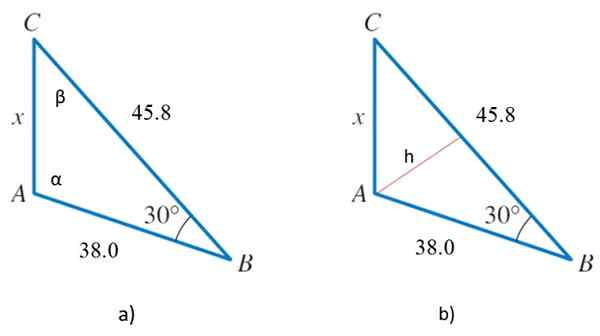Figur 2. 2a) Triangle for året løst 2 og 2b) den samme trekanten med en høyde, som vil tjene til å bestemme området. Kilde: f. Zapata.

Løsning på

Av trekanten er to tilstøtende sider kjent, hvis tiltak er 38.0 og 45.8 og vinkelen mellom dem, som er 30º, blir derfor kosinusteoremet umiddelbart brukt:

x² = 38.0² + Fire fem.8² - 2 x 38.0 x 45.8 x cos 30º = 527.18

Derfor:

x = (527.18)^1/2 = 22.96

Tegningen antyder at α> 90º og trekanten er stump, i tillegg til skrå. For å sjekke det, finner vi sidene på sidene, slik det ble gjort i forrige øvelse:

22.96² = 527.18

38.0² = 1444.00

Fire fem.8² = 2097.64

Vinkelen α er større enn 90 º hvis det er sant enn kvadratet på motsatt side: 45.8²  Det er større enn summen av rutene på de andre sidene, som er 22.96² + 38.0².

Kan tjene deg: Eksponentlover

La oss se om det skjer:

527.18 + 1444.00 = 1971.2

Faktisk:

2097.64> 1971.2

Derfor er vinkelen α større enn 90º.

Løsning b

Nå kan vi bruke bryststeoremet for å finne en av de manglende vinklene. Vi kommer til å heve det for vinkel β:

Sen 30º / 22.96 = sin β / 38

Sen β = 38 x (sen 30º / 22.96) = 0.8275

β = Arcsen (0.8275) = 55.84º

Den manglende vinkelen kan bli funnet å vite at summen av de indre vinklene til en hvilken som helst trekant er 180º. Derfor:

55.84º + 30º + α = 180º

α = 94.16º

Hvis du er foretrukket, kan du også bruke kosinusteoremet for å finne kosinus i vinkelen som er mellom to tilstøtende sider. Når Coseno Arc -funksjonen brukes til å bestemme vinkelen.

Resultatene kan variere litt i desimalene, ifølge avrundingen som er utført.

Løsning c

Omkretsen P er konturen til figuren, tilsvarer summen av målene på de tre sidene:

P = 22.96 + 38.00 + 45.80 = 106.76 vilkårlige enheter.

Løsning d

Formelen for å beregne området til en hvilken som helst trekant er:

A = (1/2) x base x høyde

Vi må velge en av sidene som base og bestemme høyden. For eksempel å velge den siden som måler 45.8, vi trekker høyden h Inntil toppunkt A, som er den røde linjen i figur 2B.

Ved å gjøre dette deler vi den opprinnelige trekanten i to rektangler, begge med h som en vanlig kateto. Noen av dem serverer, siden vi kjenner en skarp side og vinkel.

Vi kommer til å ta den som har hypotenusa lik 38, en kategori som måler h, som er høyden som ble søkt og den akutte vinkelen lik 30º.

Ved hjelp av de trigonometriske grunnene til den akutte vinkelen 30º bestemmer vi verdien av h:

Sen 30º = kateto motsatt av 30º / hypotenusa = h / 38

H = 38 x sen 30º = 19

Derfor:

A = (1/2) x 45.8 x 19 = 435.1 vilkårlige områder i området.

Vi kunne ha valgt en annen side som base, for eksempel side 38, i så fall høyden h Det er annerledes, siden en annen rektangel -trekant er dannet, men resultatet av området er det samme. Det forblir som trening for leseren å sjekke det.

- Øvelse 3

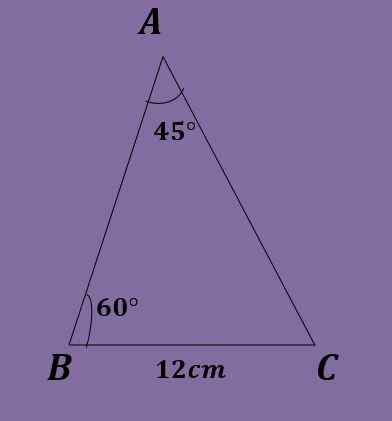
Gitt en ABC -trekant som A = 45º, B = 60º og A = 12 cm, beregner de andre trekantdataene.

Kan tjene deg: tegn på gruppering

Løsning

Ved å bruke det er summen av de indre vinklene til en trekant lik 180º den må:

C = 180º-45º-60º = 75º.

De tre vinklene er allerede kjent. Deretter fortsetter vi å bruke brystloven for å beregne de to sidene som mangler.

Ligningene som oppstår er 12 / uten (45º) = b / uten (60º) = C / uten (75º).

Fra den første likheten kan du fjerne "B" og få det:

B = 12*uten (60º)/uten (45º) = 6√6 ≈ 14.696cm.

Du kan også fjerne "C" og få det:

C = 12*sin (75º)/sin (45º) = 6 (1+√3) ≈ 16.392cm.

- Oppgave 4

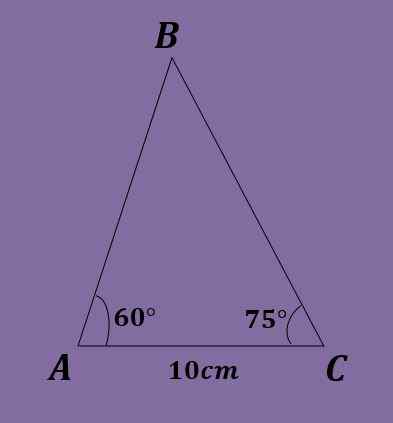
Gitt trekanten ABC slik at A = 60º, C = 75º og B = 10 cm, beregner de andre trekantdataene.

Løsning

Som året før må du b = 180º-60º-75º = 45º. I tillegg må du bruke brystloven du må / uten (60º) = 10 / uten (45º) = C / uten (75º), hvor det oppnås at A = 10*uten (60º) / uten (45º) = 5 √6 ≈ 12.247 cm og c = 10*sin (75º)/uten (45º) = 5 (1+√3) ≈ 13.660 cm.

- Oppgave 5

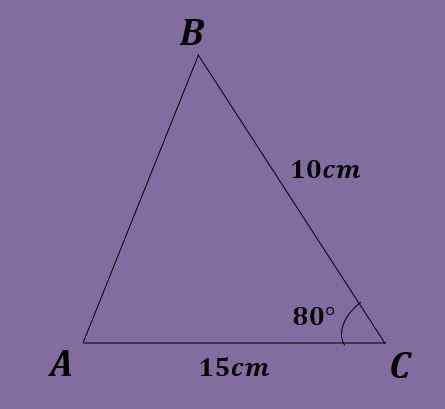
Gitt trekanten ABC slik at A = 10cm, B = 15cm og C = 80º, beregner de andre trekantdataene.

Løsning

I denne øvelsen er bare en vinkel kjent, derfor er det ikke mulig å starte som det ble gjort i de to foregående øvelsene. I tillegg kan ikke brystloven brukes fordi ingen ligning kan løses.

Derfor brukes loven til Cosenos. Du må:

C² = 10²+15² - 2 (10) (15) COS (80º) = 325 - 300*0.173 ≈ 272.905 cm,

Slik at C ≈ 16.51 cm. Nå, når du kjenner de 3 sidene, brukes brystloven og det oppnås at:

10 / uten (a) = 15 / uten (b) = 16.51cm /uten (80º).

Herfra, når klar B er uten (b) = 15*uten (80º)/ 16.51 ≈ 0.894, noe som innebærer at B ≈ 63.38º.

Nå kan det oppnås at A = 180º - 80º - 63.38º ≈ 36.62º.

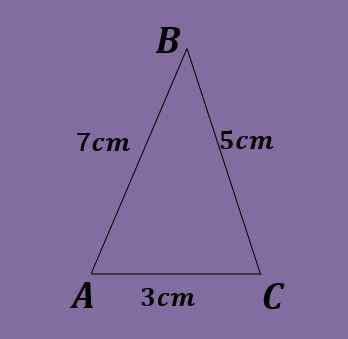
- Oppgave 6

Sidene av en skrå trekant er a = 5cm, b = 3cm og c = 7cm. Beregn vinkelene på trekanten.

Løsning

Igjen kan ikke brystloven brukes direkte, siden ingen ligning vil tjene til å oppnå verdien av vinklene.

Ved å bruke loven om kosinuset må du c² = a² + b² - 2ab cos (c), fra hvor når cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2 og derfor c = 120º.

Nå kan brystloven brukes og dermed oppnå 5/uten (a) = 3/uten (b) = 7/uten (120º), hvor b kan tømmes b og oppnå det uten (b) = 3* uten (120º )/7 = 0.371, slik at b = 21.79º.

Endelig beregnes den siste vinkelen ved å bruke den A = 180º-130º-21.79º = 38.21.

Referanser

1. Clemens, s. Geometri med applikasjoner. Addison Wesley.
2. Ibáñez, p. 2010. Matematikk III. Cengage Learning.
3. Jiménez, r. Matematikk II: Geometri og trigonometri. 2. Utgave. Pearson.
4. Matematikk for deg. Stump trekant. Gjenopprettet fra: matematikk for.WordPress.com.
5. Stewart, J. 2007. Forkalkning. 5. plass. Utgave. Cengage Learning.