Perfekt firkantet trinomial

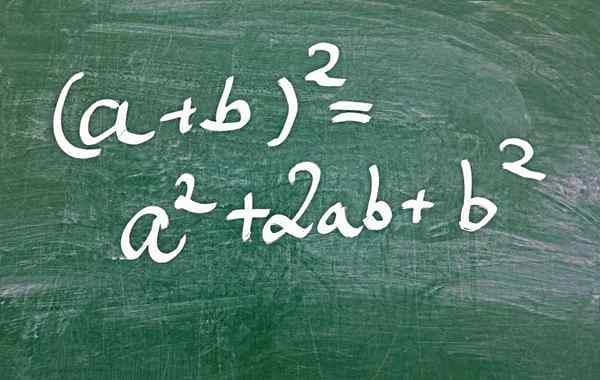Figur 1.- En av måtene å få en perfekt firkantet trinomial er gjennom summen av summen

Hva er den perfekte firkantede trinomial?

Den perfekte firkantede trinomialen er at polynomet av tre begreper, hvorav to er perfekte firkanter av mengdene A og B og er foran med samme tegn, mens den tredje termen er nøyaktig det doble produktet av A og B, og kan være av et annet tegn.

En perfekt firkantet trinomial oppnås av kvadrat summen eller forskjellen på en binomial og algebraisk, formen er formen som følger:

til² ± 2 ∙ AB + B²

Som det fremgår, inneholder den perfekte firkantede trinomialen:

• To ikke -limilære kvadratiske vilkår foran med samme tegn: a² og b²
• En tredje periode 2 ∙ AB, som er det doble produktet av de firkantede røttene til de kvadratiske begrepene, og som kan inngås et positivt eller negativt tegn.

Perfekte firkantede trinomials kan være en eller mer variabel. Følgende trinomial er for eksempel en perfekt firkant av en variabel:

• x² + 6x + 9

Merk at de første begrepene (x²) og tredje (9) er henholdsvis firkantet av mengdene som kalles A og B. Faktisk, x² Det er kvadratet med x og 9 er kvadratet med 3. På denne måten kan du skrive følgende:

a = x

B = 3

Og den gjenværende begrepet er det doble produktet av X og 3:

6x = 2 ∙ 3 ​​∙ x

Når verifiseringen er gjort, er det sikkert at denne trinomialen er perfekt firkant.

Eksempler

Figur 2.- Eksempler på perfekte firkantede trinomialer. Kilde: f. Zapata.

Perfekte firkantede trinomialer vises også i to eller flere variabler, for eksempel:

4x² + 4xy + og²

Det er en trinomial i to variabler: "x" og "y". Det kan sikre at det er en perfekt firkantet trinomial, siden den presenterer to kvadratiske termer:

4x² = (2x)²

og² = (y)²

Og det gjenværende begrepet er det doble produktet av de respektive firkantede røttene: "2x" og "y":

Kan tjene deg: orthoedro: Formler, område, volum, diagonal, eksempler

4xy = 2 ∙ 2x ∙ og

Trinomialene som er presentert så langt er grad 2 i variabelen "X", men de trenger ikke nødvendigvis å være slik. Følgende trinomial er grad 4 i "X":

9x⁴ - 30x²YZ + 25Y²z²

Det er lett bekreftet at dette er en perfekt firkantet trinomial. Den første termen er den perfekte 3x kvadrat², Siden (3x²)² = 9x⁴.

Begrepet 25y²z² er lik (5yz)². Endelig er den gjenværende perioden 2 ∙ 3x²∙ 5yz = 30 x²og z.

På den annen side er trinomialene som er vist nedenfor ikke perfekte firkantede trinomials:

• x²  + 8x - 16

Det er ikke en perfekt firkantet trinomial fordi 16, selv om det er 4², Det er gitt et negativt tegn, mens det andre kvadratiske begrepet (x²) er positivt.

• x²  - 15x + 25

Det er heller ikke en perfekt firkantet trinomial, for selv om den har to kvadratiske termer: x² og 5², Begrepet 15x er ikke lik 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Denne trinomialen er ikke perfekt firkant, siden den bare inneholder et kvadratisk begrep: 4x² = (2x)².

Kvadrat for en sum og kvadrat av en forskjell

Perfekte firkantede trinomialer oppnås ved å utvikle to typer bemerkelsesverdige produkter:

• Summen av summen.
• Kvadratet med forskjellen.

Først oppnås utviklingen fra distribusjonseiendommen, siden det å heve den firkantede binomialen betyr å multiplisere den med seg selv:

(A ± B)² = (a ± b) × (a ± b) = a² ± a ∙ b ± b ∙ a + b² = a² ± 2A ∙ B + B²

Det trinomiale som oppnås er et resultat som er husket med bare litt praksis og er en slags snarvei som letter utviklingen, og det er derfor det kalles et bemerkelsesverdig produkt.

Kan tjene deg: transcendente tall: hva er, formler, eksempler, øvelser

Følgende trinomials oppnås enkelt med bemerkelsesverdig produkt, uten å bruke distribusjonseiendommer på nytt.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 og² +20xy + 4x²

Faktorisering av en perfekt firkantet trinomial

En hyppig og nødvendig operasjon i algebra er faktoriseringen av den perfekte firkantede trinomialen, som trinomialen uttrykkes som kvadratet for en sum eller en subtraksjon av to begreper (en binomial).

Det er den omvendte operasjonen å utvikle det bemerkelsesverdige produktet, siden det å ha den resulterende trinomialen, er ideen å oppnå binomialen som gir opphav til det når den stiger til 2.

For eksempel i den tidligere analyserte 4x perfekte firkantede trinomial² + 4xy + og², Hva er binomialen at når det er kvadratet, gir det deg?

De respektive firkantede røttene til de kvadratiske begrepene er:

√ (4x²) = 2x

Som tilsvarer: 4x² = (2x)²

√ (og²) = y

Tilsvarer å si det: og² = (y)²

Derfor:

4x² + 4xy + og² = (2x + y)²

Og hva er binomialen som har sin opprinnelse den perfekte firkantede trinomial 9x⁴ - 30x²YZ + 25Y²z²? Igjen blir de firkantede røttene til de kvadratiske begrepene trukket ut:

√ (9x⁴) = 3x²

√ (25 og²z²) = 5yz

Så:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25Y²z²

Løste øvelser

Oppgave 1

I hver av de følgende trinomialene, fullfør tomt med begrepet som mangler å være en perfekt firkantet trinomial:

a) m² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Løsning på

I henhold til formelen til det bemerkelsesverdige produktet:

Kan tjene deg: komplementære vinkler: Hvilket og hvordan de blir beregnet, eksempler, øvelser

(A ± B)² = A² ± 2A ∙ B + B²

Av trinomialen:

m² + 18m + _____

Det følger at:

a = m (slik at² = m²)

I tillegg er den sentrale termen: 2 ∙ A ∙ B = 2M ∙ B = 18M, derfor B = 9 og kvadratet er 9² = 81. Guy av formelen til det bemerkelsesverdige produktet, trinomialen er slik:

(M + 9)² = M² + 18m + 81

• Løsning b

I denne trinomiale:

4x² - _____ + 64

Du kan vite og B:

A = √ (4x²) = 2x

B = √64 = 8

Derfor er det manglende begrepet det doble produktet av A og B:

2 ∙ ab = 2 ∙ 8 ∙ 2x = 32x

Og den etterspurte trinomialen er:

4x² - 32x + 64

• Løsning c

I trinomialen:

_____ + 30n + 25

Den første perioden mangler, men det er kjent at:

B = √25 = 5

OG

2 ∙ ab = 2 ∙ a ∙ 5 = 10a = 30n

Derfor er a = 3n og den etterspurte trinomialen:

9n² + 30n + 25

Oppgave 2

Sjekk at den neste er en perfekt firkantet trinomial og faktor det:

16y² - 24YZ + 9Z²

• Løsning

Først er det bevist at de kvadratiske begrepene er gitt av samme tegn, og deretter blir de respektive firkantede røttene funnet:

A = √ (16y²) = 4y

B = √ (9Z²) = 3Z

Da må du bekrefte om det gjenværende begrepet er det doble produktet av A og B:

2 ∙ AB = 2 ∙ 4y ∙ 3Z = 24YZ

Hvis det er det, kan trinomialen faktor som kvadratet med en forskjell, siden det sentrale uttrykket er gitt et negativt tegn:

16y² - 24YZ + 9Z² = (4y - 3z)²

Referanser

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Kates matematikkundervisning. Perfekte firkantede trinomials. Gjenopprettet fra: Katesmathlessons.com.
3. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
4. Zill, d. 2008. Preccculment med fremskritt av beregning. 4. plass. Utgave. McGraw Hill.