EN Rhomboid Det er en flat figur på fire sider, -en firkantet -som sidene og dens indre vinkler er forskjellige to til to. Derfor tilhører Rhomboid gruppen av skrå parallellogrammer.

Geometriske figurer er en del av naturen, og spesielt de fra fire sider som Rhomboid, har mange applikasjoner innen arkitektur og design.

Figur 1. Belysningspanelene på Allianz Arena Stadium i München, Tyskland, lyser opp med fargene på lokallaget og med hvitt lys når utvalget av det landet spiller. Kilde: Pxhere.

UP har vi en del av fasaden til Allianz Arena Football Stadium i München. De er rhomboid -paneler som lyser opp med fargene på lokal teamet.

Det er derfor en figur med mye visuell dynamikk, for i motsetning til andre kvadrilateraler, har den ingen symmetriakse. Følgende figur viser forskjellige rhomboider med varierte orienteringer i flyet.

Figur 2. Flere rhomboid med forskjellige orienteringer i flyet. Kilde: f. Zapata.

[TOC]

Romboid -egenskaper

Deretter hovedegenskapene til denne interessante geometriske figuren:

-Arknummer: 4.

-Antall hjørner: 4.

-De motsatte sidene er de samme og parallelle, men de tilstøtende sidene er ulik.

-Den har 4 interne vinkler: to akutte (mindre enn 90 º), betegnet med den greske bokstaven α og to stump (over 180º), kalt β (se figur 3).

-Ved å legge til to sammenhengende vinkler på rhomboid, oppnås 180º, derfor er α og β Tillegg.

-Summen av de 4 indre vinklene er lik 360º.

-En diagonal er et segment som starter fra et toppunkt og slutter i motsatt toppunkt.

-Punktet der diagonalene til det rhomboid krysset kalles barycenter.

-Rhomboid -diagonalene har forskjellige størrelser.

Om diagonalene til Rhomboid er det noen viktige detaljer som vi vil diskutere nedenfor.

Kan tjene deg: i påvente av en linje: formel og ligninger, representasjon, eksempler

Diagonaler av Rhomboid

Det er veldig viktig å understreke at diagonalene til rhomboidene ikke er bisektriske, det vil si at de ikke deler de indre vinklene til figuren i to like deler.

Diagonalene er ikke vinkelrett på hverandre. Vi kan imidlertid enkelt beregne dem med kosinusteoremet. Dermed den viktigste diagonal d_M I rhomboid i figur 3 er:

D_M = √ (a² + b² - 2.AB.cos β)

Og den mindre diagonale d_m Jeg ville vært:

D_m = √ (a² + b² - 2.AB.cos α)

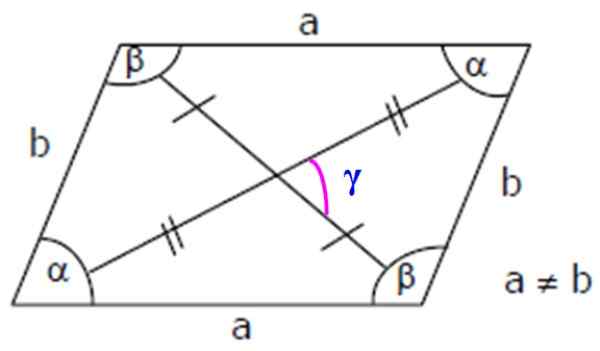Figur 3. Romboid -elementer: Sider, indre og diagonale vinkler. Kilde: Wikimedia Commons.

Viktig: Ettersom α og β er supplerende, blir det oppfylt at:

sin α = sin β

cos α = -cos β

Disse egenskapene til trigonometriske grunner må tas i betraktning når du løser øvelsene.

Hvordan ta ut omkretsen og området

For å finne omkretsen og området vil vi gi navn til sidene av rhomboid, disse vil være til og b. Vi har også høyden på rhomboid, kalt h, som er linjen trukket fra en av toppunktene og rettet vinkelrett mot motsatt side av figuren.

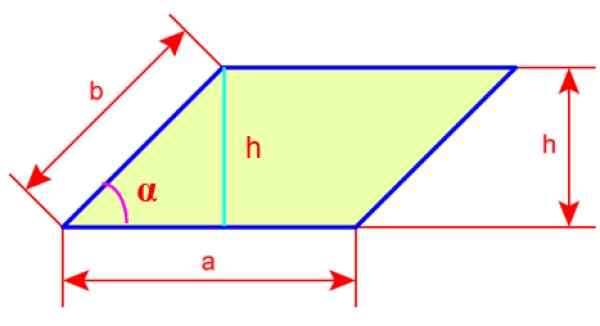Figur 4. Sider og rhomboid høyde. Kilde: Wikimedia Commons.

Omkretsen av Rhomboid

Omkretsen til Rhomboid beregnes ved å legge til lengdene på sine fire sider. La oss ringe P til omkretsen, da:

P = 2A + 2B

Vi kan også uttrykke det gjennom:

P = 2 (A+B)

Omkrets å vite høyden

Hvis vi ser bra ut, kan høyden H bestemmes fra trekanten til venstre i figur 4. Side B ville være hypotenusen og høyden H katetoet imot vinkelen α, derfor:

sin α = motsatt / hypotenusa kateto

O vel:

sin α = h / b

Så fjerner vi B:

b = h / sin α

Vi erstatter i omkretsen P:

P = 2 [A + (h / sin α)]

Romboid -området

Rhomboid -området er målet på overflaten. Og siden det er et parallellogram, er dets område A gitt av det velkjente uttrykket:

Kan tjene deg: Vanlig faktor for gruppering av begreper: eksempler, øvelser

A = base x høyde

At ifølge figur 3 og 4 er det uttrykt gjennom:

A = a x h

Område som kjenner begge sider og en indre vinkel

Ved å bruke den grunnleggende trigonometrien i forrige seksjon, finner vi likeverdige uttrykk for Rhomboid -området:

h = b. sin α

Da er området slik:

A = a. b. sin α

Husker hva vi sa ovenfor om tilleggsvinklene, kan vi erstatte Sen α med Sen β om nødvendig.

Område som kjenner diagonalene og vinkelen mellom dem

Til slutt, hvis vi kjenner diagonalene d_M og d_m, Pluss vinkelen γ mellom dem (se figur 3), kan området beregnes med halvproduktet til diagonalene gjennom brystet i nevnte vinkel:

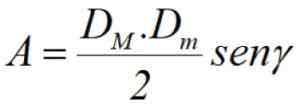
Trening løst

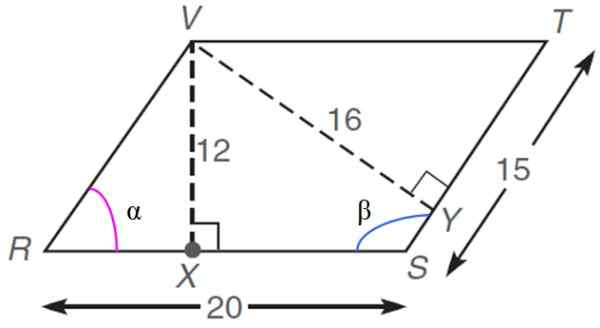
I det følgende rhomboid, hvis dimensjoner er gitt i vilkårlige enheter eller.til., finne:

a) Omkretsverdien

b) området

c) interne vinkler α og β

d) Lengden på RX -segmentet

e) Målet på hver av diagonalene

Løsning på

Omkretsen P er:

P = 2 (A + B)

Vi identifiserer først verdiene til a og b:

A = 20

B = 15

Vi erstatter formelen og beregner:

P = 2. (20 + 15) = 70 u.til.

Løsning b

Diagrammet gir høyde H = 12 u.A, derfor kan området beregnes med formelen:

A = a x h

A = 20 x 12 u.til.² = 240 u.til.²

Uansett den valgte enheten for å måle sidene og høyden, uttrykkes alltid området i kvadratiske enheter.

Det samme resultatet hvis du får når du beregner området med den andre høyden på rhomboid, som er verdt 16 u.til. Faktisk:

A = 16 x 15 u.til.² = 240 u.til.²

Løsning c

Vinkelen α kan beregnes gjennom:

Det kan tjene deg: posisjonstiltak, sentral tendens og spredning

h = b. sin α

Siden H- og B -verdier er kjent, derfor:

α = Arcsen (h/b) = Arcsen (12/15) = 53.13

Husker at α- og β -vinkler er supplerende, er det oppfylt:

α + β = 180º ⇒ β = 180 - 53.13. = 126.87º

Løsning d

RX -segmentlengden beregnes enkelt, fordi det er nok informasjon til å finne den. For eksempel gjennom:

Rx = RV . cos α = 15 . Cos 53.13. u.til. = 9 u.til.

Også gjennom Pythagoras -teoremet gjennom rektangelets trekant på sider 15 og 12 u.til:

(RV)² = (Rx)² + h²

Rydde lengden på rentesegmentet:

Rx = √ [(RV)² - h²] = √ [15² - 12²] = √81 = 9

Løsning e

Målet på en av diagonalene, for eksempel diagonalen som blir sammen med toppunktet R og T, som er en viktig diagonal, er gitt av kosinusteoremet, som tidligere forklart, så vi erstatter verdier der:

D_M = √ (20² + 25² - 2. tjue. femten .Cos 126.87º) = 37.22 u.til.

For den mindre diagonalen:

D_m = √ (20² + 25² - 2. tjue. femten .Cos 53.13.) = 25.79 u.til.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Baldor, a. 1973. Geometri og trigonometri. Sentralamerikansk kulturell redaksjon.
3. OG. TIL. 2003. Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
4. Jiménez, r. 2010. Matematikk II. Geometri og trigonometri. Andre utgave. Prentice Hall.
5. Vanlige polygoner. Gjenopprettet fra: kompis.Ingeniørfag.USAC.Edu.Gt.
6. Universformler. Rhomboid. Gjenopprettet fra: Universoformulas.com.
7. Wikipedia. Rhomboid. Gjenopprettet fra: er.Wikipedia.org.