Vi forklarer hva og hva som er spredningstiltakene, og vi gir flere eksempler

Hva er spredningstiltak?

De målinger av spredning eller av variasjon, i statistikk, måle hvor mye en fordeling av data fra verdien av et sentralt tiltak beveger seg, for eksempel gjennomsnittet eller aritmetisk gjennomsnitt. Verdien er alltid positiv og normalt forskjellig fra 0, bortsett fra i tilfelle av identiske data.

Hvis et spredningstiltak gir en liten verdi, betyr det at dataene ligger veldig nær gjennomsnittet, men hvis de er store, betyr det at dataene er mer spredt, derfor, vekk fra gjennomsnittet.

Spredningstiltak er veldig viktige fra det statistiske synspunktet, ikke bare som aritmetiske indikatorer for datavariasjon, men som en uvurderlig hjelp når du vil forbedre kvaliteten, både i fremstilling av produkter og i levering av tjenester.

Eksempel på dette er oppmerksomhetsrekkene i bankene. Gjennomsnittlig tid på å forsinke kunder når de lager en unik rad og deretter distribueres på billettkontoret, er den samme som om de lager individuelle linjer foran hver.

Imidlertid er spredningen lavere i enkeltrekken, noe som betyr at individuell oppmerksomhetstid er veldig lik hver klient. Kunder har erklært at de føler seg mer komfortable på denne måten, selv om gjennomsnittlig omsorgstid er den samme i begge modaliteter.

Hoveddispersjonstiltak

De viktigste er: rang, varians, standardavvik og variasjonskoeffisient.

Område

Rangering av et datasett er definert til forskjellen mellom maksimal verdi x_Maks og minimumsverdien x_min av hele:

Rang = r = maksimal verdi - minimumsverdi = x_Maks - x_min

Kan tjene deg: hva er tallene for? De 8 hovedbrukene

Området er raskt å beregne, men det er veldig følsomt for ekstreme verdier, og har ulempen å ikke ta hensyn til mellomverdier. Derfor brukes det bare til å ha en innledende, ganske omtrentlig ide om datadispersjonen.

Eksempel på rang

Dette er en liste over antall orkaner i Atlanterhavet i løpet av de siste 14 årene:

8; 9; 7; 8; femten; 9; 6; 5; 8; 4; 12; 7; 8; 2

Maksimumsverdidataene er 15, og minimumsverdien er derfor 2:

R = maksimal verdi - minimumsverdi = x_Maks - x_min = 15 - 2 = 13 orkaner

Forskjell

Dette tiltaket brukes til å sammenligne hver av dataene med gjennomsnittet av settet, og det beregnes ved å legge til forskjellene, kvadrathøyt, mellom hver verdi med gjennomsnittet og dele med det totale antall verdier.

Være:

-Gjennomsnittet: μ

-Enhver verdi, tilhørende datasettet: x_Yo

-Det totale antall observasjoner: n

Betegner variansen til en populasjon som σ², Uttrykket for å beregne det er:

Og når en prøve av en populasjon tas, er det foretrukket å beregne variansen på denne måten:

Der prøvevariansen er betegnet med S, og gjennomsnittet som x med stolpe, for å forlate bruken av greske bokstaver til befolkningen. Årsaken til å dele mellom n-1, i stedet for n, er at prøvevaransen ikke undervurderer befolkningen, hva som alltid skjer når den deler seg mellom n.

På den annen side er ideen om å plassere hver forskjell mellom data og gjennomsnittet å forhindre dem i å legge dem til 0, siden noen forskjeller vil være positive og andre negative, noe som har en tendens til å avbryte summen. I stedet er firkanter alltid positive.

Det kan tjene deg: Frekvens sannsynlighet: Konsept, hvordan det beregnes og eksempler

Derfor er varians alltid positiv, selv om forskjellen mellom x_Yo Og gjennomsnittet er negativt, og dens største fordelen med variansen er at den tar hensyn til hver data fra settet.

Men det har ulempen at enhetene ikke er de samme som dataene, for eksempel, hvis disse består i tider, målt på få minutter, vil variansen til settet bli gitt på få minutter til torget.

Eksempel på varians

Beregningen av variansen krever å finne gjennomsnittet. Når du tar orkannummerdataene, beregnes gjennomsnittet av:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 orkaner.Derfor er variansen:

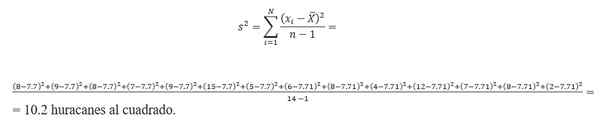
Standardavvik

For å rette opp problemet med mangel på samsvar mellom enhetene, er standardavviket definert σ, Som kvadratroten av variansen:

Og analogt, i tilfelle av et utvalg:

Det er en empirisk regel for å estimere verdien av standardavviket til et prøvedatasett, basert på området. I henhold til denne regelen er standardavviket omtrent en fjerdedel av R:

S ≈ R/4

Det har fordelen av å tillate et raskt estimat av standardavviket, siden operasjoner er mye enklere.

Standardavviket er med mye det mest brukte spredningstiltaket, så det er verdt å fremheve hovedegenskapene:

• Standardavviket indikerer hvor mye mediedataene beveger seg bort
• Det er alltid positivt, men det kan være 0 hvis alle dataene er identiske
• Jo større verdi av standardavviket, jo mer spredt er dataene
• Standardavviksenhetene er de samme som av variabelen som studeres
• Verdien endres raskt når en av dataene (eller mer) har en veldig annen verdi enn resten
• Standardavvikingsverdiene er partiske, det vil si at gjennomsnittet av standardavviket ikke er fordelt rundt gjennomsnittet, i motsetning til variansen, som ikke er -partisk.

Kan tjene deg: Acutangle Triangle

Eksempel på standardavvik

Fortsetter med eksemplet med orkaner, er standardavviket:

Eller, hvis det foretrekkes å bruke tilnærmingen til standardavviket gjennom området, oppnås en ganske nær verdi:

S = 13/4 = 3.25

Variasjonskoeffisient

Variasjonskoeffisienten er betegnet med initialene CV eller R, i noen tekster, og både for en populasjon, og for en prøve, relaterer standard og gjennomsnittlig avvik, i prosent:

O vel:

Ligningene er gyldige så lenge gjennomsnittet er forskjellig fra 0.

Som regel er variasjonskoeffisienten avrundet til en enkelt desimal, og brukes til å sammenligne data fra to forskjellige populasjoner.

Eksempel på variasjonskoeffisient

Ventetider på sekunder, for en banks kunder, blir registrert i to situasjoner: når de lager en unik rad og når de lager individuelle rekker før oppmerksomhetskontoret. Resultatene er følgende:

Begge datasettene kan sammenlignes gjennom deres respektive variasjonskoeffisient:

Enkelt rad

• Gjennomsnitt = 429 sekunder
• Avvik = 28.6 sekunder
• CV = (28.6/429) x 100 = 6.7 %

Individuelle rekker

• Gjennomsnitt = 429 sekunder
• Avvik = 109.3 sekunder
• CV = (109.3/429) x 100 = 25.5 %

Siden denne siste verdien er større, indikerer dette at det er mer variasjon i kundeservicetider når de lager individuelle rekker enn når de lager en unik rad, selv om gjennomsnittlig tid er den samme i hvert tilfelle.