Kontinuerlige variable egenskaper, eksempler og øvelser

De Kontinuerlig variabel Det er en som kan ta et uendelig antall numeriske verdier mellom to gitte verdier, selv om disse to verdiene er vilkårlig nære. De brukes til å beskrive målbare attributter; for eksempel høyde og vekt. Verdiene tatt av en kontinuerlig variabel kan være rasjonelle tall, reelle tall eller komplekse tall, selv om dette siste tilfellet er sjeldnere i statistikk. 

Hovedkarakteristikken for kontinuerlige variabler er at mellom to rasjonelle eller reelle verdier alltid kan finnes, og mellom den andre og den første kan finne en annen verdi, og så på ubestemt tid.

Figur 1. Kurven representerer en kontinuerlig fordeling og stolpene en diskret. Kilde: Pixabay

Anta for eksempel vektvariabelen i en gruppe der den største vekten har 95 kg og den laveste 48 kg vekt; Det vil være rekkevidden for variabelen og antall mulige verdier er uendelig.

For eksempel mellom 50,00 kg og 50,10 kg kan være 50,01. Men mellom 50,00 og 50,01 kan tiltaket være 50,005. Det er en kontinuerlig variabel. På den annen side, hvis det i mulige vektmålinger ble etablert en enkelt desimal nøyaktighet, ville variabelen som ble brukt være diskret.

Kontinuerlige variabler tilhører kategorien kvantitative variabler, fordi de har en numerisk verdi tilknyttet. Med denne numeriske verdien er det mulig å utføre matematiske operasjoner som spenner fra aritmetikk til metodene for uendelig beregning. 

[TOC]

Eksempler

De fleste av variablene i fysikken er kontinuerlige variabler, blant dem kan vi navngi: lengde, tid, hastighet, akselerasjon, energi, temperatur og andre.

Kontinuerlige variabler og diskrete variabler

I statistikk kan forskjellige typer variabler defineres, både kvalitative og kvantitative. Kontinuerlige variabler tilhører denne siste kategorien. Med dem er det mulig å utføre aritmetikk- og beregningsoperasjoner.

For eksempel variabelen h, Tilsvarende personer med høyde mellom 1,50 m og 1,95 m, er det en kontinuerlig variabel. 

La oss sammenligne denne variabelen med denne andre: antall ganger som er dyrt i lanseringen av en valuta, som vi vil kalle n.

Variabelen n Du kan imidlertid ta verdier mellom 0 og uendelig n Det er ikke en kontinuerlig variabel siden den ikke kan ta verdien 1.3 eller 1.5, for mellom verdiene 1 og 2 er det ingen andre. Dette er et eksempel på Diskret variabel.

Trening av kontinuerlige variabler

Tenk på følgende eksempel: En maskin produserer fosforkamper og pakker dem i boksen. To statistiske variabler er definert:

Kan tjene deg: Isobarisk prosess: Formler, ligninger, eksperimenter, øvelser

Variabel 1: L = Ploselengde.

Variabel 2: n = antall griser per boks.

Den nominelle kampens lengde er 5,0 cm med 0,1 cm toleranse. Antall griser per boks er 50 med en toleranse på 3.

a) Angi verdiene som kan ta L og N.

b) Hvor mange verdier kan du ta L?

c) Hvor mange verdier kan du ta n?

Si i hvert tilfelle hvis det er en diskret eller kontinuerlig variabel.

Løsning

Verdiene til L De forstås i intervallet [5,0-0.1; 5,0+0,1]; det vil si at verdien av L er i intervall [4,9 cm; 5,1 cm] og variabelen L Du kan ta uendelige verdier mellom disse to tiltakene. Det er da en kontinuerlig variabel.

Verdien av variabelen n er i intervallet [47; 53]. Variabelen n Det kan bare ta 6 mulige verdier i toleranseintervallet, det er da en diskret variabel.

Trening av sannsynlighetsfordeling

Hvis verdiene som er tatt av variabelen har assosiert en viss sannsynlighet for forekomst i tillegg til å være kontinuerlig, så er det en Kontinuerlig tilfeldig variabel. Det er veldig viktig å skille om variabelen er diskret eller kontinuerlig, siden sannsynlige modeller som gjelder hverandre er forskjellige.

En kontinuerlig tilfeldig variabel er fullstendig definert når verdiene de kan anta er kjent, og sannsynligheten for at hver av dem må skje.

-Oppgave 1 av sannsynligheter

Matches -fabrikken gjør dem på en slik måte at lengden på pinnene alltid er mellom 4,9 cm og 5,1 cm verdier, og null ut av disse verdiene. Det er sannsynligheten for å skaffe en pinne som måler mellom 5,00 og 5,05 cm, selv om vi også kan trekke ut en av 5.0003 cm. Er disse verdiene like sannsynlige?.

Kan tjene deg: Relativ tetthet: beregning, eksempler, øvelser

Løsning

Anta at sannsynlighetstettheten er ensartet. Deretter er sjansene for å finne en fosfor med en viss lengde listet opp:

-At en fosfor er i området [4,9; 5,1] har sannsynlighet = 1 (eller 100%), siden maskinen ikke tar kamper ut av disse verdiene.

-Å finne et fosfor som er mellom 4,9 og 5,0 har sannsynlighet = ½ = 0,5 (50%), siden det er halvparten av lengden på lengden.

-Og sannsynligheten for at kampen har lengde mellom 5,0 og 5,1 er også 0,5 (50%)

-Det er kjent at det ikke er noen fosforpinner som har en lengde mellom 5,0 og 5.2. Sannsynlighet: null (0%).

Sannsynligheten for å finne en pinne i et visst område

La oss nå observere følgende sannsynligheter P for å skaffe pinner hvis lengde er mellom l₁ og jeg₂:

 P = (l₂ -l₁) /(L_Maks - L_min)

-P at en kamp har en lengde mellom 5,00 og 5,05 er betegnet som P ([5.00; 5.05]):

P ([5,00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P at cerrilloen har lengde mellom 5,00 og 5,01 er:

P ([5,00; 5,01]) = (5,00 - 5,01)/(5,1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P at cerrilloen har lengde mellom 5000 og 5 001 er enda lavere:

P (5000; 5,001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Hvis vi fortsetter å redusere intervallet for å nærme oss mer og mer til 5,00, er sannsynligheten for at en pinne har nøyaktig 5,00 cm null (0%). Det vi har er sannsynligheten for å finne en kamp innen et visst område.

Sannsynligheten for å finne flere pinner i et bestemt område

Hvis hendelsene er uavhengige, er sannsynligheten for at to pinner i et visst område er et produkt av deres sannsynlighet.

-Sannsynligheten for at to pinner er mellom 5,0 og 5,1 er 0,5*0,5 = 0,25 (0,25%)

-Sannsynligheten for at 50 pinner er mellom 5,0 og 5,1 er (0,5)^50 = 9 × 10^-16, som er nesten null.

-Sannsynligheten for at 50 pinner er mellom 4,9 og 5,1 er (1)^50 = 1 (100%)

-Oppgave 2 av sannsynligheter

I det forrige eksemplet ble antagelsen gjort at sannsynligheten er ensartet i det gitte intervallet, men det er ikke alltid tilfelle.

Kan tjene deg: Hydrostatisk trykk: Formel, beregning, eksempler, øvelser

Når det gjelder den virkelige maskinen som produserer pinnene, er muligheten for at pinnen er i den sentrale verdien større enn i en av de ekstreme verdiene. Fra det matematiske synspunktet er dette modellert med en funksjon f (x) kjent som sannsynlighetstetthet.

Sannsynligheten for at tiltaket er mellom A og B beregnes med den definerte integralen av funksjonen f (x) mellom A og B. 

Anta som et eksempel at vi ønsker å finne funksjonen f (x), som representerer en jevn fordeling mellom verdier 4.9 og 5.1 i oppgave 1. 

Hvis sannsynlighetsfordelingen er ensartet, er f (x) lik konstant C, som bestemmes å ta integralen mellom 4,9 og 5,1 av C. Siden dette integralet er sannsynligheten, så må resultatet være 1.

Figur 2. Ensartet sannsynlighetstetthet. (Egen utdyping)

Noe som betyr at C er verdt 1/0,2 = 5. Med andre ord, den ensartede sannsynlighetstetthetsfunksjonen er f (x) = 5 hvis 4,9≤x≤5,1 og 0 ut av dette området. Figur 2 viser en jevn sannsynlighetstetthetsfunksjon.

Legg merke til som i intervaller av samme bredde (for eksempel 0,02) er sannsynligheten den samme i sentrum som på slutten av det kontinuerlige variableområdet L (Pickle Length).

En mer realistisk modell ville være en sannsynlighetstetthetsfunksjon som følgende:

-f (x) = -750 ((x-5.0)^2-0.01) hvis 4,9≤x≤5,1

-0 utenfor dette området 

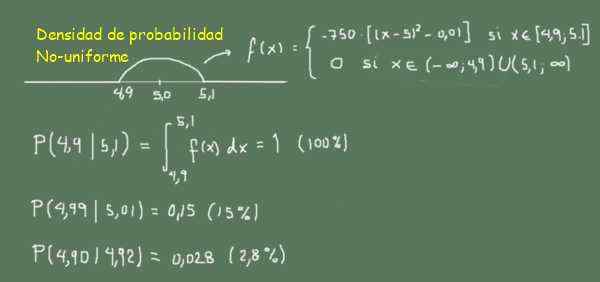Figur 3. Ikke -ulik sannsynlighetstetthetsfunksjon. (Egen utdyping)

I figur 3 kan det observeres som sannsynligheten for å finne pinner mellom 4,99 og 5,01 (bredde 0,02) er større enn å finne pinner mellom 4,90 og 4,92 (bredde 0,02)

Referanser

1. Dinov, Ivo. Diskrete tilfeldige variabler og sannsynlighetsfordelinger. Gjenopprettet fra: Stat.UCLA.Edu
2. Diskrete og kontinuerlige tilfeldige variabler. Gjenopprettet fra: OCW.mit.Edu
3. Diskrete tilfeldige variabler og sannsynlighetsfordelinger. Gjenopprettet fra: hjemmeside.DDMS.Uiowa.Edu
4. H. Peshro. Introduksjon til sannsynlighet. Gjenopprettet fra: Sannsynlighetskurs.com
5. Mendenhall, w. 1978. Statistikk for administrasjon og økonomi. Ibero -American redaksjonell gruppe. 103-106.
6. Tilfeldige variable problemer og sannsynlighetsmodeller. Gjenopprettet fra: UGR.er.
7. Wikipedia. Kontinuerlig variabel. Gjenopprettet fra Wikipedia.com
8. Wikipedia. Statistisk variabel. Gjenopprettet fra Wikipedia.com.