Matte

Proporsjonal variasjon

Proporsjonal variasjon

Hva er proporsjonal variasjon?

Den proporsjonale variasjonen mellom to variabler "x" og "y" finner sted når den andre også ved å multiplisere en av dem med en konstant. Mange situasjoner i den virkelige verden kan beskrives ordentlig med dem.

Proporsjonaliteten mellom variablene kan være direkte eller omvendt. I direkte proporsjonalitet er forholdet av typen:

y = k ∙ x

Eller tilsvarende:

K = y/x

Hvor k kalles en konstant proporsjonalitetskonstant enten forholdet mellom proporsjonalitet. Legg merke til at hvis "x" øker, "y" gjør det i samme andel, og hvis "x" avtar, vil det også "y". Når forholdet mellom variablene er grafer, oppnås en rett linje som går gjennom opprinnelsen til koordinatsystemet (se øvelsen løst senere).

Den direkte variasjonen kan også forekomme mellom den ene variabelen og den ene kraften til den andre, for eksempel "y" kan være direkte proporsjonal med x2, x3 og så.

På den annen side, i omvendt proporsjonalitet, er variablene koblet gjennom uttrykket:

x ∙ y = k

Dette uttrykket betyr at produktet av variablene er en konstant. Når du tegner forholdet mellom variablene er en hyperbola. Hvis produktet av en variabel med den ene kraften til den andre er konstant, representerer det også et tilfelle av omvendt proporsjonalitet, for eksempel:

x2∙ y = k; x3∙ y = k ..

Eksempler

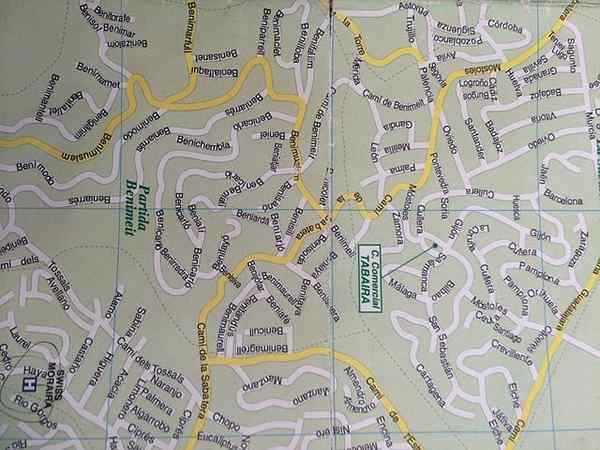En anvendelse av proporsjonal variasjon er kartoppsett

Mange fysikk og kjemi er uttrykt matematisk som proporsjoner. For eksempel kraften som utøver en fjær og forlengelsen av det samme, forholdet mellom trykket og volumet i en gass ved konstant temperatur, perioden med en enkel pendel og kvadratroten av dens lengde og mange flere. Når du kjenner modellen som styrer fenomenet, kan du finne ut atferden din for enhver verdi av variablene.

Kan tjene deg: eksistens og unikhet teorem: demonstrasjon, eksempler og øvelser

Og ikke bare det, de gjelder også i utallige situasjoner som disse:

  • Gi mønsteret til et plagg av mindre størrelse til større størrelse (eller omvendt).
  • I konverteringsfaktorer, for å flytte fra en enhet til en annen, for eksempel kilometer til miles, gallons til liter og mer.
  • Beregn ingrediensene i en oppskrift for 6 personer som vet kravet til 4 personer.
  • Bestem mengden av visse skatter i samsvar med inntektene som er oppnådd.
  • I beregningen av enkel interesse.
  • Når du tegner fly på skala.
  • Når du må beregne prisen på en mengde produkter som kjenner enhetsprisen.
  • I likheten mellom trekanter.

Neste, i detalj, er det to interessante situasjoner der proporsjonale variasjoner gjelder:

Eksempel 1

På skalaen til en by måler Hermitage Avenue 3.2 cm, å være dens virkelige lengde på 400 m. På den annen side må gaten til La Fuente, som virkelig måler 180 m lang, trekke med et proporsjonalt kortere slag. Hva er størrelsen på hjerneslaget?

Uttalelsen tilbyr fullstendig informasjon fra Ermita Avenue: La den virkelige lengden på alléen og ℓ dens lengde på flyet, ettersom variasjonen er av direkte proporsjonalitet, må den:

L = k ∙ ℓ

Fra dataene om Hermitage Avenue kan du vite verdien av proporsjonalitetskonstanten K, men før det er nødvendig å legge igjen alle lengdene i de samme enhetene:

3.2 cm = 0.032 m

Så:

400 m = k ∙ 0.032 m

Derfor er proporsjonalitetskonstanten:

Kan tjene deg: Hva er elementene i lignelsen? (Deler)

K = 400/0.032 = 12500

Nå er det kjent at:

L = 12500 ∙ ℓ

Dette resultatet tolkes som følger: Lengden på gatene på dette kartet er 12500 ganger mindre enn dens virkelige lengde. Derfor måler linjen til gaten til La Fuente:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Eksempel 2

En analytiker har følgende tabell over verdier for variablene "x" og "y" oppnådd eksperimentelt og ønsker å vite om disse dataene passer til en modell av direkte proporsjonal variasjon eller en av omvendt proporsjonal variasjon.

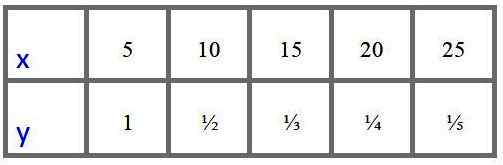
Hva bør du gjøre for å vite?

For det første blir det observert at når "x" øker, avtar "y", så den mistenker en omvendt proporsjonalitet, i alle fall, for å sikre at analytikeren har muligheten til å vurdere om kvotient og/x er konstant (proporsjonal variasjon direkte) eller hvis produkt x.og er konstant (omvendt proporsjonal variasjon).

Testing med det første alternativet:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Det konkluderes med at det ikke er en direkte proporsjonal variasjon, fordi kvotienten og/x gir forskjellige verdier for hvert par data.

Vi må sjekke om produktet X ∙ er konstant:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Og som produktet x ∙ y = 5 er det konkludert med at variasjonen er av omvendt proporsjonalitet.

Denne informasjonen tjener til å kjenne verdier som ikke er i tabellen, for eksempel hva som vil være verdien av "y" når x = 30?

Fra x ∙ y = 5 blir "y" ryddet og erstattet x = 30:

y = 5/x

y = 5/30 = 1/6

Trening løst

Hvis en stoffmåler koster 6.75 dollar, og å vite at prisen er direkte proporsjonal med mengden meter å kjøpe, finn:

Det kan tjene deg: Antiderivat: Formler og ligninger, eksempler, øvelser

a) Det algebraiske uttrykket som knytter variablene "pris til $" og "antall meter stoff".

b) Forbered en verdibord med priser for 3, 6, 9, 12, 15 og 18 meter stoff.

c) Grafer de oppnådde verdiene.

Svar til

La "y" den variable "prisen til $" og "x" variabelen "mengde meter stoff". Som direkte proporsjonalt, må du:

y = k ∙ x

For x = 1 meter, y = 6.$ 75, derfor k = 6.75 $/meter. Dette er enhetsprisen på stoffet, prisen på noe annet "X" -stoff oppnås ved å multiplisere med denne verdien, da er det algebraiske uttrykket som er søkt:

y = 6.75 ∙ x

Svar b

Verditabellen med priser til $ for 3, 6, 9, 12, 15 og 18 meter er:

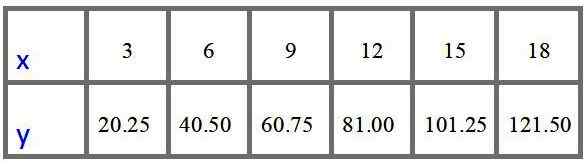
Svar c

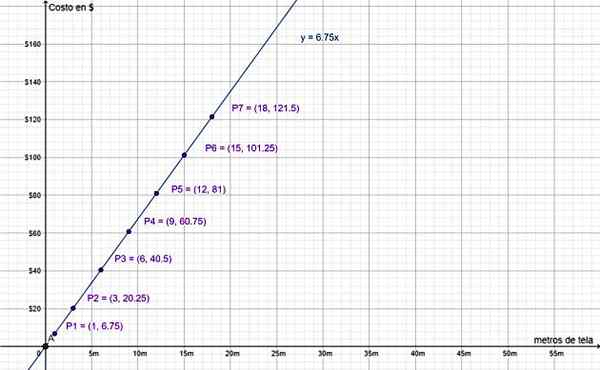
Til slutt bekrefter grafen over verdiene i den forrige tabellen at det er en direkte proporsjonal variasjon:

Kostnaden til $ og mengden meter stoff er direkte proporsjonale mengder. Kilde: f. Zapata.

Merk at verdien (0,0) er inkludert, siden linjen y = 6.75 ∙ X passerer gjennom opprinnelsen til koordinatsystemet, som forklart før. Det er fornuftig, siden det å ikke kjøpe et kjøp tilsvarer å kjøpe 0 m stoff, hvis verdi er 0 $.

Referanser

  1. Larson, r. 2012. Før-skulptur. 8. Utgave. Cengage Learning.
  2. Public Education Secretariat of Mexico. Den proporsjonale variasjonen. Hentet fra: PPS.K12.Eller.oss.
  3. Stewart, J. 2007. Forkalkning: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
  4. Unam. Studieguider: Matematikk i. Gjenopprettet fra: Dirre.Unam.MX.
  5. Zill, d. 2008. Forkalkning med beregningsfremskritt. 4. plass. Utgave. McGraw Hill.