Fysisk

Vector Director Equation of the Line, Solved Exercises

Vector Director Equation of the Line, Solved Exercises

Det forstås av Regissørvektor Den som definerer retningen på en linje, enten i flyet eller i verdensrommet. Derfor kan en vektor parallell med linjen betraktes som en direktør for det samme.

Dette er mulig takket være et aksiom av euklidisk geometri som sier at to punkter definerer en linje. Deretter definerer det orienterte segmentet som danner disse to punktene også en vektordirektør for den linjen.

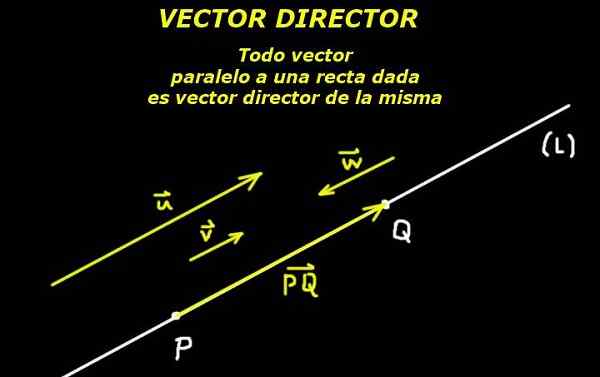Figur 1. Vektordirektør for en linje. (Egen utdyping)

Gitt et poeng P tilhører linjen (L) og gitt en regissørvektor eller Av den linjen er linjen fullstendig bestemt.

[TOC]

Ligning av linjen og direktørdirektør

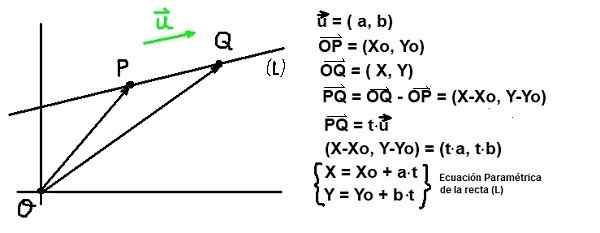
Figur 2. Ligning av linjen og direktørdirektør. (Egen utdyping)

Gitt et poeng P av koordinater Spørsmål: (Xo, meg) og en vektor eller Direktør for en linje (L), Alle poeng Q av koordinater Spørsmål: (X, Y) må oppfylle den vektoren Pq være parallell med deg. Denne siste tilstanden er garantert hvis Pq Det er proporsjonalt med eller:

Pq = T⋅eller

I forrige uttrykk t Det er en parameter som tilhører reelle tall.

Hvis de kartesiske komponentene i Pq og av eller Den forrige ligningen er skrevet som følger:

(X-xo, y-yo) = t⋅ (a, b)

Hvis komponentene i vektorlikestilling er lik følgende par av ligninger:

X - xo = a⋅t      og   Og - meg = b⋅t 

Parametrisk ligning av linjen

Koordinatene X og OG av et punkt som tilhører linjen (L) som går gjennom et koordinatpunkt (Xo, meg) Og det er parallelt med Regissørvektor eller= (a, b) De bestemmes ved å tilordne reelle verdier til variabel parameter t:

X = xo + a⋅t; Y = meg + b⋅t

Eksempel 1

For å illustrere betydningen av den parametriske ligningen på linjen, tar vi som direktørvektor

Kan tjene deg: bølgende optikk

eller = (a, b) = (2, -1) 

og som et kjent punkt på linjen punktet 

P = (xo, meg) = (1, 5). 

Den parametriske ligningen på linjen er:

X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞

For å illustrere betydningen av denne ligningen viser figur 3, der parameter t endrer verdi og punkt Q  av koordinater (X, y) Ta forskjellige posisjoner på linjen.

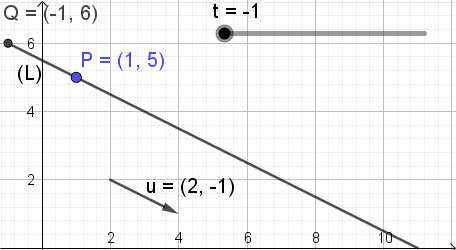Figur 3. Pq = t u. (Egen utdyping)

Linjen i vektorform

Gitt et punkt P på linjen og dens direktørdirektør eller ligningen på linjen kan skrives i en vektorform:

OQ = Op + λ⋅eller 

I den forrige ligningen som er et hvilket som helst punkt, men som tilhører linjen og λ Et reelt tall.

Vektorligningen på linjen er anvendelig for et hvilket som helst antall dimensjoner, til og med en hyper-eret kan defineres.

I det tre -dimensjonale tilfellet for en regissørvektor eller= (a, b, c) og et poeng P = (xo, me, zo), Koordinatene til et generisk punkt Q = (x, y, z) Tilhører linjen er:

(X og z) = (Xo, i, zo) + λ⋅ (a, b, c)

Eksempel 2

Vurder igjen linjen som har som direktørdirektør  

eller = (a, b) = (2, -1) 

og som et kjent punkt på linjen punktet 

P = (xo, meg) = (1, 5). 

Vektorligningen til denne linjen er:

(X, y) = (1, 5) + λ⋅ (2, -1) 

Kontinuerlig form for linjen og direktørvektoren

Starter fra den parametriske formen, rydde og matcher parameteren λ du har:

(X-xo)/a = (y-yo)/b = (z-zo)/c

Dette er den symmetriske formen for linjeligningen. Jeg føler det til, b og c De er komponentene i direktørvektoren.

Eksempel 3

Tenk på linjen som har som direktørdirektør  

eller = (a, b) = (2, -1) 

og som et kjent punkt på linjen punktet 

Kan tjene deg: Hva er strømmen? (Med eksperiment)

P = (xo, meg) = (1, 5). Finn sin symmetriske form.

Den symmetriske eller kontinuerlige formen er av linjen er:

(X - 1)/2 = (y - 5)/( - 1)

Generell form for linjeligningen

Det er kjent som den generelle formen for linjen i XY -planet til ligningen som følgende struktur har:

A⋅x + b⋅y = c

Uttrykket av den symmetriske formen kan skrives om slik at den har den generelle formen:

B⋅x - A⋅y = B⋅xo - A⋅o

Sammenligning med den generelle formen for linjen gjenstår: 

A = b, b = -a og C = B⋅xo - A⋅o 

Eksempel 3

Finn den generelle formen for linjen hvis direktør er u = (2, -1)

 Og hva som går gjennom punkt P = (1, 5).

For å finne den generelle formen kan vi bruke de gitte formlene, men en alternativ vei vil bli valgt.

Vi begynner med å finne den doble W -vektoren til U -vektoren, definert som vektoren som oppnås ved å utveksle komponentene i U og multiplisere med -1 den andre:

W= (-1, -2)

Den doble vektoren W tilsvarer en rotasjon i 90 ° i planen til direktørens direktør v.

Vi multipliserer klatring W med (X, y) og med (Xo, meg) Og vi stemmer overens:

(-1, -2) • (x, y) = (-1, -2) • (1, 5)

-X -2y = -1 -2⋅5 = -11

Endelig gjenværende:

X + 2y = 11

Standardform på linjeligningen

Det er kjent som standardform for linjen i XY -planet, den som har følgende struktur:

Y = m⋅x + d

hvor m representerer skråningen og D -avskjæringen med aksen og.

Gitt direktøren u = (a, b) vektor, er skråningen m b/a.

Og D oppnås ved å erstatte X og Y av det kjente punktet XO, ME:

I = (b/a) xo + d.

Kort sagt, m = b/a y d = meg -(b/a) xo

Merk at skråningen M er kvotienten mellom komponenten og av regissøren og komponenten x av det samme.

Kan tjene deg: Rotasjonsbalanse: Formler og ligninger, eksempler, øvelser

Eksempel 4

Finn standardform på linjen hvis direktør er u = (2, -1) 

Og hva som går gjennom punkt P = (1, 5).

M = -½ og d = 5 -( -½) 1 = 11/2

Y = (-1/2) x + 11/2

Løste øvelser

-Oppgave 1

Finn en vektordirektør for linjen (L) som er skjæringspunktet mellom planet (π): x - y + z = 3 og planet (ω): 2x + y = 1.

Skriv deretter den kontinuerlige formen for linjen på linjen (L).

Løsning

Fra flyligningen (ω) klaring y: y = 1 -2x

Deretter erstatter vi i planligningen (π):

X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x

Så parameteriserer vi x, vi velger parameteriseringen x = λ

Dette betyr at linjen har en vektorligning gitt av:

(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)

som kan skrives om som:

(X, y, z) = (0, 1, 4) + λ (1, -2, -3)

Med det som er klart at vektoren eller = (1, -2, -3) er en rett administrerende vektor (L).

Den kontinuerlige formen for linjen (L) er:

(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)

-Oppgave 2

Gitt 5X -flyet + til Y + 4z = 5 

og linjen hvis ligning er x/1 = (y-2)/3 = (z -2)/(-2)

Bestemme verdien av til slik at flyet og linjen er parallell.

Løsning 2

Vektoren n = (5, a, 4) er en normal vektor til planet.

Vektoren eller = (1, 3, -2) er en rett manager.

Hvis linjen er parallell med flyet, så n • v = 0.

(5, til, 4)•(1, 3, -2) = 5 +3til -8 = 0 ⇒ til= 1.

Referanser

  1. Fleming, w., & Varberg, D. OG. (1989). Prealculus matematikk. Prentice Hall Ptr.
  2. KOLMAN, f. (2006). Lineær algebra. Pearson Education.
  3. Lojal, j. M., & Viloria, n. G. (2005). Flat analytisk geometri. Mérida - Venezuela: Venezuelansk redaksjon C. TIL.
  4. Navarro, Rocio. Vektorene. Gjenopprettet fra: Bøker.Google.co.gå.
  5. Pérez, ca. D. (2006). Prequalculus. Pearson Education.
  6. Prenowitz, w. 2012. Grunnleggende konsepter av geometri. Rowman & Littlefield.
  7. Sullivan, m. (1997). Prequalculus. Pearson Education.