Karakteristiske enhetsvektorer, hvordan få det ut, eksempler

De enhetsvektorer er de hvis modul, størrelse eller størrelse er lik den numeriske verdien en. Enhetsvektorene er nyttige for å indikere retningen til andre ikke -enhetsvektorer.

Husk at vektorer er matematiske enheter som matematisk representerer de fysiske størrelsene som er avhengige av retning, for eksempel styrke, hastighet, akselerasjon og andre.

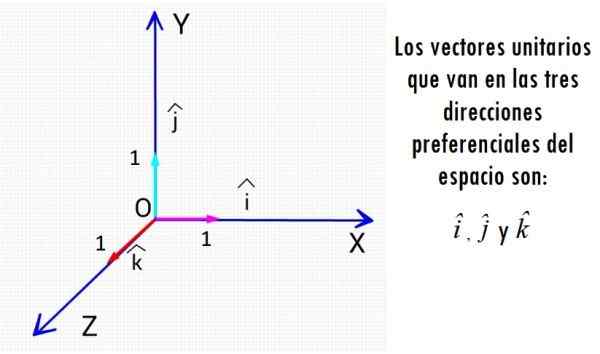
De mest kjente enhetsvektorene er de tre vektorene som går i retningene til de kartesiske aksene. Kilde: f. Zapata.

Uansett den fysiske størrelsesorden som er assosiert, er enhetsvektorene enheter som mangler måleenheter og deres størrelse er alltid 1, et rent tall.

For eksempel er hastigheten på en partikkel som beveger seg på 3 m/s og går i positiv retning av den kartesiske X -aksen, betegnet: v = (3 m/s) Yo, Hvor det fetme bokstaven brukes til å betegne vektorbeløpene. I dette eksemplet modulen til v Det er 3 m/s og enhetsvektormodulen Yo er 1 (uten enheter).

[TOC]

Modul, retning og mening

Gitt det viktige. På tidspunktet for å representere et vektorbeløp, er det nødvendig å tydelig indikere disse aspektene.

Nå kan en enhetsvektor ha noen retning og betydningen som er foretrukket, men størrelsen må alltid være lik 1.

Enhetsvektorer brukes til å indikere en privat adresse i verdensrommet eller i flyet. Hvis vi for eksempel må samarbeide med alle kreftene som virker langs den horisontale aksen, siden en enhetsvektor i den retningen hjelper oss å skille disse kreftene fra andre rettet i en annen retning.

Og for å skille dem fra ikke -enhetsvektorer, brukes BOLD vanligvis på trykk og plasser en circumflex -aksent på toppen, for eksempel:

Det kan tjene deg: Stasjonær statsteori: Historie, forklaring, nyheter

For håndskrevne tekster er det nok å plassere Circumflejo til å forstå at det er en enhetsvektor.

Kjennetegn på en enhetsvektor

Matematisk enhetsvektoren:

Det er et element som tilhører et vektorrom ℛ av dimensjon n, slik at |v| = 1, der stolpene betyr "modul".

Så vi kan fastslå det:

-Den enhetlige vektorkodulen er alltid 1, det spiller ingen rolle om det er en styrke, hastighet eller annen vektor.

-Enhetsvektorer har en viss retning, så vel som retning, for eksempel enhetsvektoren i vertikal retning, noe som kan være fornuftig opp eller ned.

-Enhetsvektorer har et opprinnelsespunkt. Når det er representert av et kartesisk koordinatsystem, sammenfaller Point sammen med systemets opprinnelse: (0.0) hvis det er planet eller (0.0.0) hvis vektoren er i det tre -dimensjonale rommet.

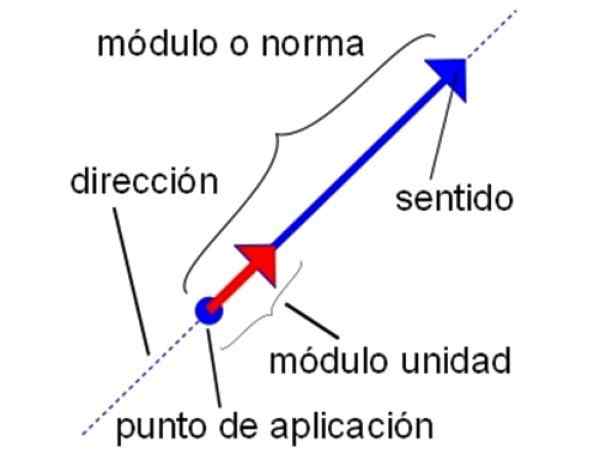Egenskapene til enhetsvektoren. Kilde: Wikimedia Commons.

-Også med enhetsvektorene kan alle operasjoner av sum, subtraksjon og vektormultiplikasjon som er laget av vanlige vektorer utføres. Derfor er det gyldig å multiplisere enhetsvektoren med en skalar, samt utføre punktproduktet og kryssproduktet.

-Med en enhetsvektor i en viss retning, kan andre vektorer også uttrykkes som også er orientert i den retningen.

Enhetsvektorene i verdensrommet

For å uttrykke en hvilken. Hver av de tre foretrukne romens retninger har sin egen enhetsvektor.

La oss gå tilbake til eksemplet med kreftene rettet langs den horisontale aksen. Dette er x -aksen, som har to muligheter: retning til høyre og retning til venstre. Anta at det er en enhetsvektor på x -aksen og rettet til høyre, som vi kan betegne gjennom noen av disse skjemaene:

Kan tjene deg: Thomson Atomic Model: Kjennetegn, postulater, subatomiske partikler

Noen av dem er gyldige. Anta at en styrke F₁ av størrelsesorden 5 n langs denne aksen og rettet mot høyre, kan en slik kraft uttrykkes som:

Hvis kraften ble rettet langs x -aksen, men i motsatt retning, det vil si til venstre, kan et negativt tegn brukes til å etablere denne forskjellen.

For eksempel ville en 8 n størrelsesraft, plassert på x -aksen og rettet mot venstre være slik:

Eller noe:

Og for vektorer som ikke er rettet langs de kartesiske aksene, er det også en måte å representere dem på med tanke på de ortogonale enhetsvektorene, gjennom deres kartesiske komponenter.

Hvordan fjerne/beregne enhetsvektoren?

For å beregne enhetsvektoren i retning av en vilkårlig vektor v, Følgende formel brukes:

Hvor:

Det er modulen eller størrelsen på vektoren v, hvis torget beregnes slik:

|v|² = (v_x)² +  (v_og)²+  (v_z)²

En vilkårlig vektor når det gjelder enhetsvektoren

Alternativt vektoren v Det kan uttrykkes som følger:

Det vil si produktet av modulen med den tilsvarende enhetsvektoren. Dette er nøyaktig hva som ble gjort før, når du snakket om kraften på 5 N størrelsesorden rettet langs den positive x -aksen.

Grafisk representasjon

Grafisk sett sees det som sies i dette bildet, der vektoren v Den er i blått og den tilsvarende enhetsvektoren i sin retning er i rødt.

I dette eksemplet, vektoren v Den har en størrelse større enn for enhetsvektoren, men forklaringen er til og med gyldig hvis dette ikke skjer. Med andre ord, vi kan ha vektorer som er for eksempel 0.25 ganger enhetsvektoren.

Kan tjene deg: vekt (fysisk): beregning, enheter, eksempler, øvelser

Eksempler på enhetsvektorer

De vinkelrett enhetsvektorene I, J og K

Som vi har sett før, vinkelrett enhetsvektorer Yo, J og k De er veldig nyttige for å representere enhver annen vektor i planet eller rommet, og utføre vektoroperasjoner. Når det gjelder nevnte vektor, er en vilkårlig vektor V representert som:

v = v_x Yo + v_og J + v_z k

Hvor v_x, v_og og v_z er de rektangulære komponentene i vektoren v, som er stigninger -Bold brukes ikke til å representere dem i trykt tekst-.

Coulombs lov

Entarvektorer vises ofte i fysikk. Der har vi for eksempel Coulombs lov, som kvantitativt beskriver samspillet mellom to spesifikke elektriske ladninger.

Det indikerer at styrken F av attraksjon eller frastøtning mellom disse belastningene er proporsjonalt med produktet av dem, omvendt proporsjonal med kvadratet på avstanden som skiller dem og er rettet i retning av enhetsvektoren som fester seg med lastene.

Denne vektoren er vanligvis representert av:

Og Coulombs lov er slik, i en vektorform:

Hvor k Det er den elektrostatiske konstanten, q₁ og q₂ De er lastene og r Det er avstanden som skiller dem.

Trening løst

Finn enhetsvektoren i retning av vektoren v = 5Yo + 4J -8k, Gitt i vilkårlige enheter.

Løsning

Definisjonen av enhetsvektor ovenfor brukes ovenfor:

Men først må du beregne vektorkodulen, som ettersom den har tre komponenter, bestemmes av:

|v|² = (v_x)² +  (v_og)² +  (v_z)²

Blir:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Derfor modulen til v er:

|v| = √105

Den enhetlige vektoren som er søkt er ganske enkelt:

Som til slutt fører oss til:

v = 0.488 Yo + 0.390 J - 0.781 k

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
5. Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.