Volum

Vi forklarer hva som er volumet, dets formler, enheter, hvordan du beregner det og gir flere eksempler

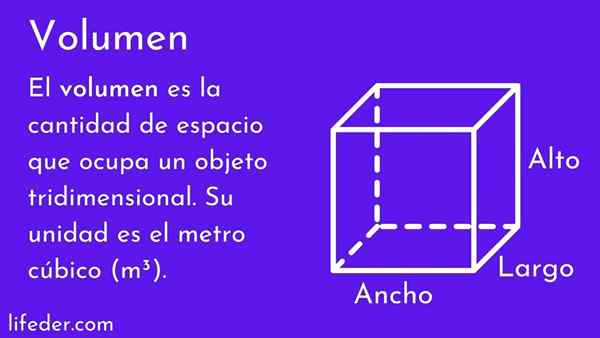
Hva er volumet?

Han volum av et legeme er den numeriske verdien som måler mengden plass okkupert av den. Den høye, bredde og dybde bestemmer volumet, jo større, jo større er det okkuperte rommet.

Volumkonseptet er av stor betydning, siden verden er tre -dimensjonal og alle objekter har bredde, høyde og dybde, derfor har de volum. Folk bruker det ofte, for eksempel ved å estimere om møblene de vil kjøpe, det passer på rommet sitt, eller om de går inn i en viss klesstørrelse.

I visse områder av vitenskap og ingeniørfag, for eksempel når du arbeider med væsker, enten væsker eller gasser, får det okkuperte volum du synker ikke. Alt dette gjør det viktig å bestemme det for mange prosesser.

Det er formler for å beregne volumet av geometriske kropper i vanlige former, for eksempel prismer, sfærer, sylindere og kjegler, for eksempel avhengig av noen av dimensjonene. Og det er også måter å finne ut volumet av uregelmessige gjenstander, som vil bli beskrevet litt senere.

Volumformler i geometriske figurer

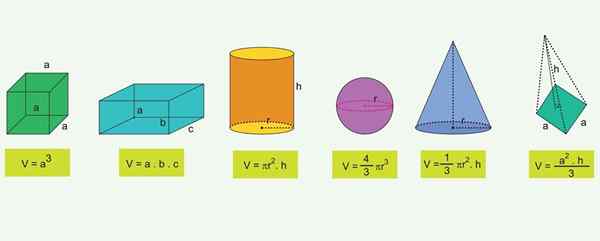Liste over de vanligste geometriske figurene og formelen til volumene deres

For de mest kjente geometriske objektene er det formler som tillater å beregne volumet:

• Kube

V = ℓ³ 

Hvor V representerer volumet og ℓ er kanten (siden) av kuben.

• Parallellpiped

En parallellpiped er en rektangulær boks med bredde "A", lang ℓ og "H" høyde. Volumet er gitt av produktet av sine tre dimensjoner:

V = a ∙ ∙ ∙ h

• Sfære

Volumet på sfæren avhenger av dens radius r:

Kan tjene deg: Nicolás Copernico

• Rett sirkulær sylinder

Volumet av den rette sirkulære sylinderen er produktet mellom området av basen og dens høyde "h". Ettersom basen er et radioalbum “R”, hvis område er A = π · R², Volumet gjenstår:

V = πr²∙ H

• Fitte

Volumet av kjeglen er en tredjedel av produktet mellom området til den sirkulære basen A og høyden H. Som a = πr², så:

• Pyramide

For en pyramide hvis baseområde er en og har en "H", er volumet gitt av:

Hvis pyramiden har en firkantet base på siden "A", som i figuren, er baseområdet til basen til² Og volumet av pyramiden er:

V = (1/3) ⋅a²⋅H

• Prisme

Prismens volum er produktet mellom området med base A og høyden "H":

V = a ∙ h

Volumenheter

I det internasjonale systemet med enheter er enheten for volum den kubiske måleren eller m³, Mens du er i Anglo -Saxon -systemet er det den kubiske foten eller FT³ (av Føtter, som på engelsk betyr "fot").

Det er mange andre enheter, i henhold til størrelsen på det okkuperte rommet. For eksempel km kubikk kilometer³ For større volumer eller kubikk millimeter mm³ For små volumer. Det er også lokale bruksenheter.

Det er også nødvendig å nevne kapasitetsenhetene, nært knyttet til volumets, som helst brukes til væsker. Den sentrale kapasitetsenheten er den liter, forkortede L, som tilsvarer en DM³ (Kubisk desimeter).

Andre enheter som er verdt å nevne er gallon, kubikk tomme, koppen og gikt, sistnevnte pleide å dosere medisiner.

Kan tjene deg: Sammenlignende metode

Hvordan måles volum?

Volumet av et legeme, som alle andre tiltak, utføres sammenlignet med et tilstrekkelig mønster, i dette tilfellet en volumenhet.

Volumenheten er definert som kuben hvis kant måler 1 enhet. Denne enheten kan være en meter, centimeter, fot, tomme eller annen. Deretter tilsvarer volumet av objektet mengden kubiske enheter okkupert av figuren og er alltid en positiv mengde.

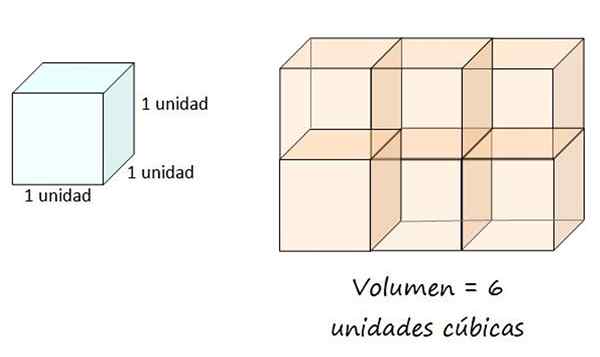En kubisk enhet er definert som volumet til en bøtte med kant lik 1, så boksen til høyre har et volum på 6 kubiske enheter. Kilde: f. Zapata.

Volum av en geometrisk kropp

Når det gjelder et geometrisk legeme som allerede nevnt, beregnes volumet gjennom passende formel, og måler dimensjonene som er angitt med formelen.

For eksempel, hvis du vil vite volumet på en sfære, er det nødvendig å måle dens diameter og med den er den radius kjent, som er halvparten av. Hvis det er en rektangulær boks, måles bredden, høyden og dybden på det samme.

Deretter blir verdiene som etterspørres i formelen satt inn, og pass på at alle enhetene er de samme, de nødvendige operasjonene blir utført, det er volumet til objektet.

Volumet av en uregelmessig kropp

Uregelmessige faste stoffer har ikke en geometrisk form, for eksempel en stein eller et blunk. Likevel kan du finne volumet ved hjelp av en gradert beholder full av vann, ved hjelp av væskeforskyvningsmetoden.

For det første bestemmes volumet okkupert av vannet, og deretter blir det uregelmessige objektet helt nedsenket, og måler det nye volumet, som er større enn originalen. Volumet av det uregelmessige objektet er forskjellen mellom dette volumet og vannet alene.

Kan tjene deg: Genie Wiley, den ville jenta som bare kjente igjen navnet hennes

For at denne metoden skal fungere, skal ikke objektet lages av noe stoff som lett blir oppløst i vannet, det må forbli helt nedsenket og selvfølgelig må du ha en gradert beholder med nødvendig størrelse for å imøtekomme den fullstendig.

Volumeksempler

Det omtrentlige volumet til noen kjente objekter er:

• Jorden: 1.08321 × 10¹² km³
• Amazonas River: 225.000 m³/s (volumet per tidsenhet kalles "flyt")
• Gizas store pyramide: 2.600.000 m³
• En fotball: 5600 cm³
• En ryggsekk: 50 DM³

Volum og masse

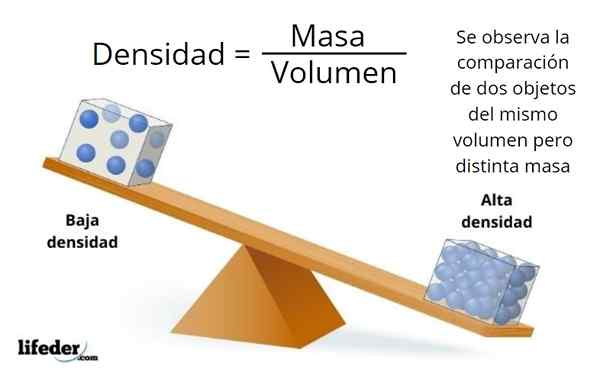
Volumet og massen er ikke synonymer, den første er knyttet til dimensjonene til objektet og den andre til mengden materie den inneholder.

Det kan være mye materie i et objekt av små dimensjoner, eller veldig lite i et stort objekt, som avhenger av tettheten av materialet, som er forholdet mellom massen og volumet til et objekt:

Løste øvelser

Oppgave 1

Beregn volumet til en rektangulær boks hvis dimensjoner er 34 cm × 22 cm × 8 cm.

• Løsning

Volumet av en rektangulær boks er ganske enkelt produktet av sine tre dimensjoner:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Oppgave 2

Basen til en firkantet pyramide har et område på 16 cm² Og høyden er 6 cm. Beregn volumet av nevnte pyramide.

• Løsning

Formelen gitt ovenfor for volumet av en pyramide brukes, kjent området for basen:

Og numeriske verdier erstattes:

V = (1/3) × 16 cm² × 6 cm = 32 cm³